最低阶频率和振型分析

按照柔度法，多自由度系统的主振型方程可表示成

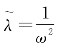式中：为系统矩阵；为与固有频率ω 相应的特征值。

为求系统的第一阶固有频率和主振型，可从式（5-55）出发，按如下步骤进行迭代求解。

（1）选取某个经过基准化的假设振型｛u｝0。矢量的基准化就是取该矢量的某一元素为1，一般取第一个元素为1，目的是使数字在迭代运算中能保持适当的大小，同时也符合第3章中的习惯。用系统矩阵前乘假设的振型，再对得到的近似振型矢量进行基准化，得

（2）如果｛u｝1=｛u｝0，则它们就是真实的第一振型，a1就是对应的特征值；如果｛u｝1≠｛u｝0，就再从｛u｝1出发，重复上述步骤，得

（3）如果｛u｝2≠｛u｝1，则继续重复上述步骤，直到

当式（5-58）中｛u｝k-1≈｛u｝k时停止。这时，特征值就等于ak，而相应的特征矢量｛φ｝1就等于｛u｝k。现在来证明这一迭代过程一定收敛到最大的特征值（对应最低频率）及其对应的特征矢量。

前面多次提及，一个任意的假设振型总可展开为，其中ci为常数；为系统的第i阶主振型，其对应的特征值为。再设所有特征值各不相等，且按大小排列有，于是，经第一次迭代后，有

则(www.xing528.com)

经第二次迭代后，有

即有

重复上述迭代过程，第k 次迭代的结果为

可见，随着迭代次数的增加，对应于的项越来越成为主导项，也就是说｛u｝k是将越来越接近于。

如果在数字计算的准确度内有｛u｝k-1=｛u｝k，亦即有

可见在相同的准确程度上就有λ～1=ak。

可写出迭代的通式为

显而易见，｛u｝k的收敛速度取决于趋于零的快慢程度。