由式![]() ,其中st表示取驻值。对于任意保守系统,固有频率的变形式可表为
,其中st表示取驻值。对于任意保守系统,固有频率的变形式可表为

其中:Vmax和T0均依赖于广义位移的振幅函数,对于不同的系统,有不同的表达式。
李兹法(也称瑞利-李兹法)的特点:可求解前几阶固有频率与振型;所求固有频率为精
确解的上限。李兹法的基本思想和步骤如下。
(1)取n 个线性无关的位移函数φi(x)(i=1,2,…,n),它们均满足位移边界条件,令
![]()
其中{a}为任意的n 维常矢量。
李兹法的基本思想是在集合式(5-38)中求瑞利商的驻值,以代替在全体可能位移φi(x)(i=1,2,…,n)中求驻值。
(2)计算式(5-37)的分子和分母,即式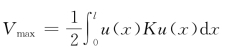 和式T0=
和式T0= ,并写为
,并写为
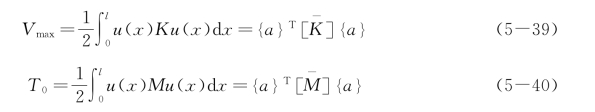
其中![]() 和
和![]() 为n×n 对称、正定矩阵,它们的元素列于表5-1。(https://www.xing528.com)
为n×n 对称、正定矩阵,它们的元素列于表5-1。(https://www.xing528.com)
表5-1 几种一维振动系统的动能和势能矩阵元素

(3)以式(5-39)、式(5-40)分别代入式(5-37)后得到
![]()
由于矢量{a}的诸分量均可独立变更,由上式可以得到代数特征值方程
![]()
(4)计算式(5-41)n 个实的、非负的特征值ω2与相应的特征矢量{a},特征矢量满足正交归一化条件。
(5)计算固有振型
![]()
李兹法的准确程度,依赖于所选基函数构成的函数空间中是否存在良好的近似固有振型,并不是依赖于个别基函数是否与固有振型接近。因而,选择基函数可以稍为随便一些,这是李兹法比瑞利法优越的地方。
在工程上应用李兹法时所取基函数的项数孢是不多的,以致只有少数几个低阶固有频率的近似值有实用意义,随着阶数的增加,近似值的误差将显著增加。因固有频率是瑞利商的逗留值,在逗留值邻近,瑞利商对自变函数的变化很不敏感。
应用李兹法的主要目的是计算系统的前一两阶固有频率,所得基本频率的近似值肯定比瑞利法得到的好,因瑞利法是李兹法当基函数仅取一项时的特殊情形。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




