多自由度系统的情况

一个n 自由度系统，根据前面章节的讨论，其刚度式运动微分方程为

设其运动微分方程的特解（即主振动）为｛y｝=｛A｝sin（ωt+α），可得到关于振幅的齐次线性方程组为

由于振幅矢量也代表了主振型矢量，它们之间只相差非零常数倍，则上式也可写为

即

式（5-1）两边前乘，得

或写为

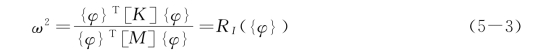
式中：称为第一瑞利商。

当式（5-3）中取为系统的各阶主振型时，瑞利商就相应地给出各阶固有频率ωi的平方（或特征值λi），即有

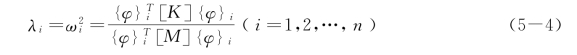
式（5-4）即为多自由度系统主振型的正交性中的公式，其分子为第i阶主刚度，分母则为第i阶主质量。

若在式（5-3）中，只是代表假设的主振型，那么由瑞利商只能得出相应固有频率的估计值。理论上，它适用于求各阶固有频率的近似值（请读者自行证明）。实际上，因为关于系统的高阶主振型很难做出合理假设，所以式（5-2）一般只用于估算系统的第一阶固有频率即基频时才能获得令人满意的精度。

注意到，系统在主振型振动中动能的最大值为

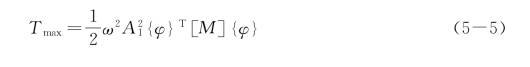
而弹性势能（应变能）的最大值为

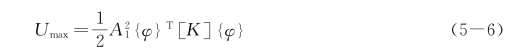
可见式（5-2）右端刚好等于，而左端刚好等于。所以，瑞利法也常称为瑞利能量法。

从柔度式分析出发，可得到另一种形式的关于系统固有频率的估算式。由前面的章节可知，系统关于主振型矢量的柔度式齐次线性方程组为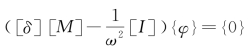，即

式（5-7）两边前乘，得

或写为

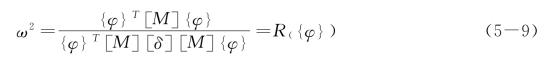
式中：R（｛φ｝）称为第二瑞利商。

当式（5-7）中的｛φ｝取为系统的主振型时，R（｛φ｝i）也就给出相应的特征值λi，即有

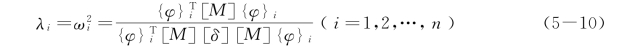
因此，第二瑞利商也可用来估算系统的固有频率。

关于式（5-8），也可以给出相应的能量解释。根据动静法，系统主振动的位移可视为由相应的惯性力所产生。系统的惯性力可表示为，由此惯性力引起的位移为，则根据功能原理，此时系统的势能为

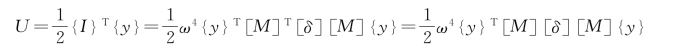
因而系统势能的最大值为

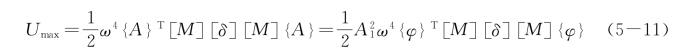
可见式（5-8）的右端等于，而其左端仍然是。

下面证明，对于任意的假设主振型，恒有

由前面章节的讨论可知，一个n自由度正定系统必定存在n个正特征值λi，不妨假设它们可由小到大地排列成λ1＜λ2＜…＜λn。对应于这n 个特征值，可确定n 个特征矢量｛φ｝i，它们是互相线性独立的，因而可构成n 维线性空间的一个完备基底。正如第3章主振型的正交性中所指出的，任何一个假设的振型矢量都可展开为各个特征矢量的线性组合，即有

式中：ci为组合系数。

此时两个瑞利商分别成为

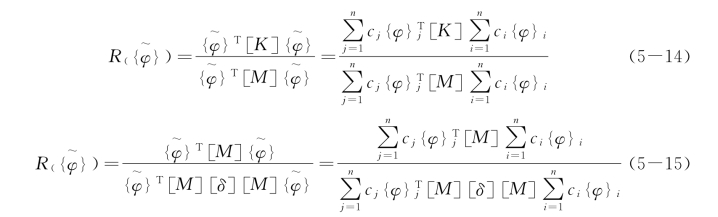
根据主振型的正交性公式，并且由式（5-7）知

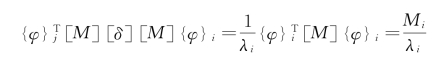(www.xing528.com)

则以上的瑞利商的表达式简化为

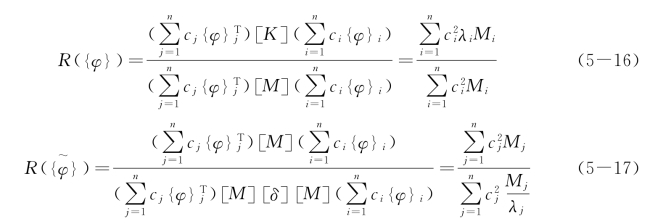
因此不等式（5-12）可写成

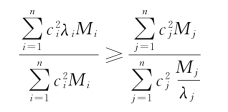
上式可等价地表示为

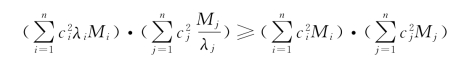
将上式写为

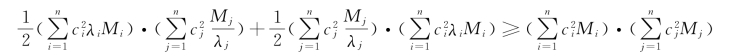
即

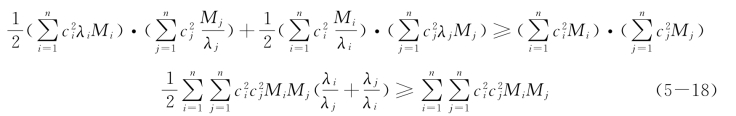
由初等数学中的不等式a2+b2≥2ab知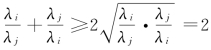，由此可见，不等式（5-18）恒成立，反推回去就证明了不等式（5-12）的正确性。

现在再来证明，用两个瑞利商来估算系统的基频时，结果总是偏大，也就是总给出基频的上限估计值，或者说精确的基频是这些估计值的下限。实际上，对于一个合理假设的第一主振型，用式（5-13）表示时，总有

由式（5-16）和式（5-17），得

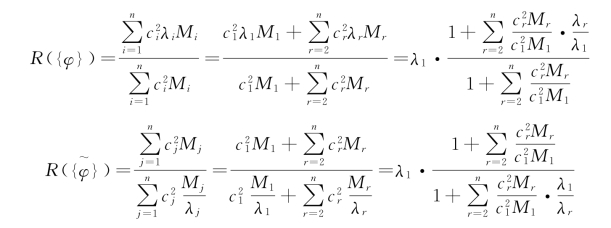
由于λ1λr（r=2，3，…，n），上面的两个瑞利商右端的分式均大于1。当满足假设条件式（5-19）时，这两个分式的值又都非常接近于1。所以说，这两个瑞利商给出的都是基频的上限估计值。而由式（5-12）可见，由第二瑞利商给出的估计值将比第一瑞利商R（｛φ｝）的更接近于真实值。

此结论从物理意义方面也不难解释，要使系统按假设的第一主振型做简谐振动，必须要给系统附加约束，将使系统的刚度增加，因此算出的基频的近似值偏大。于是在选择近似结果时，最小的那个近似值最接近真实值，应是最好的。

以上对多自由度系统介绍了两种形式的瑞利能量法。它们各有所长，前者适用于刚度矩阵已知的情形，后者则适用于柔度矩阵已知的情形。一般来说，前者较为简便，后者较为准确。

【例1】如图5-1所示的扭振系统，k1=3k，k2=2k，k3=k，J1=2J，J2=1.5J，J3=J，试用瑞利法求系统基频的估计值。

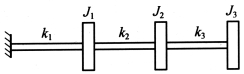
图5-1

【解】根据第3章中链状结构的刚度矩阵和柔度矩阵公式，此系统的刚度矩阵和柔度矩阵分别为

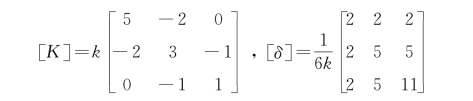
系统的质量矩阵为

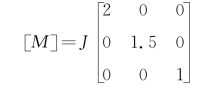
现分别用两种瑞利商求系统基频的近似值。不妨先粗糙地取假设的第一主振型为，由此得

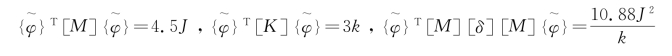
则由式（5-3），得

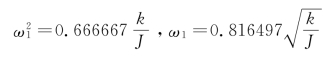
与精确值相比，误差很大，偏高37.73%。而由式（5-9），得

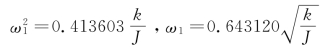
此结果比前面的结果要准确得多，与精确值相比偏高8.48%。

如果选取假设的第一主振型为，由此得

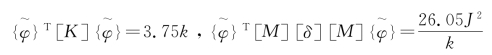
则由式（5-3），得

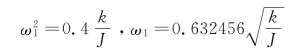
此结果比前面方案中第一瑞利商结果有所改进，与精确值相比误差下降为偏高6.68%。而由式（5-9），得

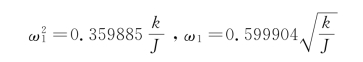
此结果比前面的第二瑞利商结果又准确许多，与精确值相比偏高1.12%。

再取“静变形曲线”为假设振型，即同时在每个圆盘上作用同方向的静转矩，转矩值之比等于圆盘的转动惯量之比。此题中在3个圆盘上同时作用比值为1∶0.75∶0.5的转矩，则三个圆盘的转角之比为1∶1.833333∶2.5，因此假设振型为2.500000｝T，由此得

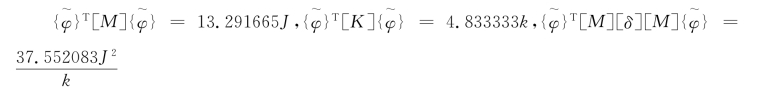
则由式（5-3），得

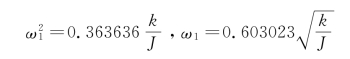
此结果的精度已很高，误差仅为+1.72%。而由式（5-9），得

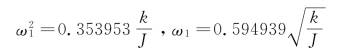
此结果精度更高，仅仅偏高0.35%。可见取静变形曲线作为假设的第一振型，用两个瑞利商求得的基频的静定都是较高的，在下面无限自由度系统的瑞利法中还会利用此特点。