主坐标的运动微分方程及解析

与多自由度系统的振型叠加法类似，梁的动位移可表示为

式中：Yi（x）为梁的第i个主振型函数，qi（t）为第i个主坐标（权函数）。

将式（4-96）代入运动方程式（4-95），得

对式（4-97）两边各项乘以Yj（x），沿梁的全长积分，并利用主振型函数对质量和刚度的正交关系，得

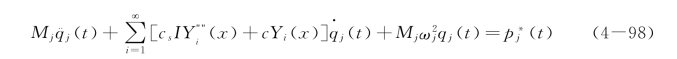
式中：第j个主质量Mj和主刚度Kj分别为

对其他非齐次边界条件的梁，主质量和主刚度的表达式可参照振型函数的正交性确定。第j个广义力为

在式（4-98）中，左边第二项是与阻尼有关的项，要使运动微分方程解耦，应设法使阻尼满足关于振型函数的正交性条件。常用的一种方法是假设阻尼与质量和刚度成正比，即

式中：a，b为比例常数。

将此阻尼假设条件代入式（4-98），并利用振型函数的正交性，得

即

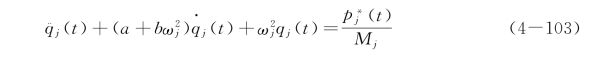
将式（4-103）表示为

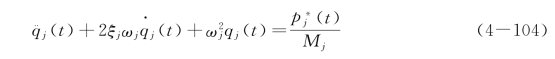
这就是解耦了的第j个主坐标的运动微分方程，它与单自由度系统的有阻尼强迫振动微分方程完全相同。其中ξj 代表第j阶振型的阻尼比，它的表达式为

显然，它与多自由度系统中比例黏性阻尼比的表达式相同，实际上，式（4-101）也为比例黏性阻尼假设。(www.xing528.com)

在多自由度系统的振型叠加法中已给出了方程式（4-104）的解的表达式，以及比例常数a，b的确定方法与计算公式，此处不再赘述。利用振型函数的正交性关系，得到主坐标的初始条件为

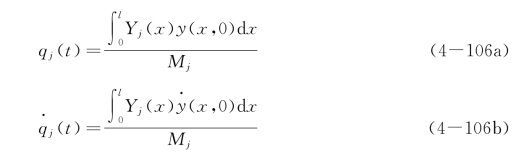
求出各个主坐标qj（t）之后，即可由坐标变换关系式（4-96）计算梁的动位移y（x，t），且在实际问题中，通常只取前面几阶振型的贡献就足够准确了。若需计算梁的动内力，可利用梁的内力与挠度的关系

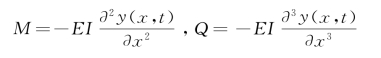
与第3章中类似，高阶振型对内力的影响比对位移的影响大，计算内力应比计算位移适当地多取几阶振型。

以上是针对梁的横向弯曲振动，讨论其有阻尼强迫振动的振型叠加法。对弦的横向振动、杆的纵向振动以及圆轴的扭转振动的情况，用振型叠加法计算它们的有阻尼强迫振动的过程与梁的情况类似。

【例4】如图4-15所示的均匀简支梁在x=c处作用有一正弦激励力P sinθt作用，求梁的动响应。

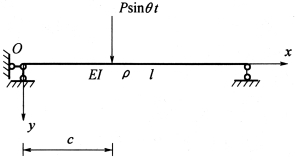
图4-15

【解】前面已求得等截面简支梁的固有频率和振型函数分别为

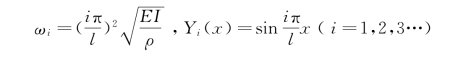
设梁的挠度为

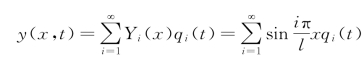
梁的各阶主质量为

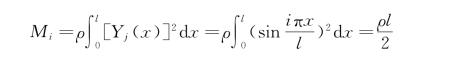
即等截面简支梁的各阶主质量相同。

当梁上的动荷载为集中力时，有两种处理方法：一是将集中力视为2ε长度（以x=c为中心）上的均布荷载，在最终的动位移结果中令ε→0；二是直接利用狄拉克-δ 函数将集中力表示为分布力p（x，t）=P sinθt·δ（x-c），则梁的各阶广义力为

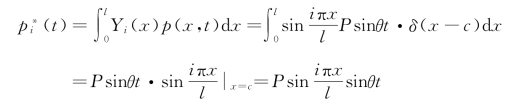
由于不计阻尼，主坐标的运动微分方程对应于零初始条件的解为

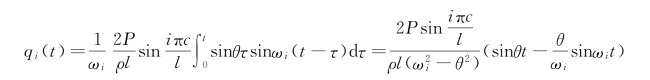
故梁的动响应为