如何导出薄板振动微分方程？

弹性薄板（Sheet）是指厚度比平面尺寸小得多的弹性体。在板中，与两表面等距离的平面称为中面。为了描述板的振动，建立一直角坐标系，其（x，y）平面与中面重合，z 轴垂直于板面。对板横向振动的分析基于下述基尔霍夫（Kirchhoff）假设：

（1）微振动时，板的挠度远小于厚度，从而中面挠曲为中性面，中面内无应变；

（2）垂直于平面的法线在板弯曲变形后仍为直线，且垂直于挠曲后的中面；该假设等价于忽略横向剪切变形，即γyz=γxz=0；

（3）板弯曲变形时，板的厚度变化可忽略不计，即εz=0；

（4）板的惯性主要由平动的质量提供，忽略由于弯曲而产生的转动惯量。

设板的厚度为h，材料密度为ρ，弹性模量为E，泊松比为μ，中面上的各点只做沿z 轴方向的微幅振动，运动位移为ω。下面根据虚功原理导出薄板振动微分方程。

薄板上任意点a（x，y，z）的位移为

根据虎克（Hook）定律，沿x，y 方向的法向应力和在板面内的剪切应力为

于是得到板的势能表达式

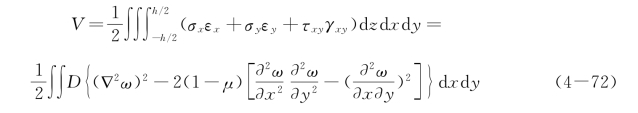
式中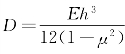：为板的抗弯刚度。板的动能为

考虑作用于板上的载荷和边界力，对于作用于板上的分布载荷q（x，y，z），其虚功可表示为

对于边界力，设板的边界曲线为x=x（s），y=y（s），这里s为弧长。边界上点的外法线单位向量和切向单位向量记为n 和τ，在边界上各点作用有弯矩Mn、横向力Qn和扭矩Mτ，如图4-13所示。这些边界力的虚功为

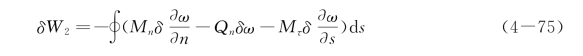
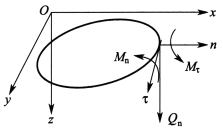
图4-13 边界载荷

根据变分方程

并利用格林（Green）公式

(www.xing528.com)

可得

式中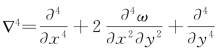：为直角坐标系中的二重拉普拉斯算子，θ为边界线的外法线和x 轴之间的夹角。因δω 任意，和δω 相互独立，因此可得到板的振动微分方程

对于简支-自由边以及自由边情形，还可由式（4-77）得到相应的动力边界条件，不再赘述。

对于长为a，宽为b的矩形薄板，可采用分离变量法求解。设

代入方程式（4-78），可得出

分离为

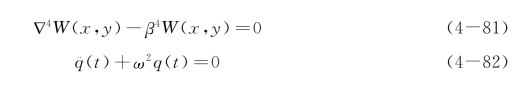
式中

如果板的四边均为简支，可设满足边界条件的试探解

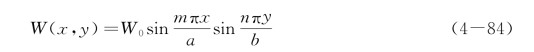
代入方程式（4-81），得到板的固有频率方程

代入式（4-83），得到固有频率

相应的固有振型函数为

当a/b为有理数时，矩形板的固有频率会出现重频；对应重频的固有振型，其形态不是唯一的。若令m=n=1，则在x=0，a 和y=0，b四条边上的点没有振动位移；若令m=2，n=1，则除了板的四条边界线外，在x=a/2时也有z=0，故在x=a/2上的点没有振动位移。通常将x=a/2这条线称为节线。若取m=1，n=2，则y=b/2成为节线。对于矩形板而言，节线总和四边平行。

至于其他边界条件的矩形板或其他形状的板，目前尚未得到显式的解析解。关于各种近似求解方法的内容看参考专著或文献。