【摘要】：该微元的变形考虑了弯矩和剪力的影响，忽略弯矩与剪力之间的相互影响。设梁的单位长的转动惯量为J，由动力学定律可得将式、式代入式和式得到对于均质等截面梁，从方程式和方程式中消去θ得到这就是均质等截面梁考虑剪切变形与转动惯量影响时的自由振动方程。
前面所讨论的梁的振动问题是以简单梁为基础的，所得到的频率和振型函数随着解次的增高其准确性将下降。因此，当分析跨度短而截面高的梁，或者分析细长梁的高阶振型时，就必须考虑剪切变形（Shear Deformation）与转动惯量（Rotary Inertia）的影响。
在梁上取微元d x，如图4-11所示。该微元的变形考虑了弯矩和剪力的影响，忽略弯矩与剪力之间的相互影响。设弯矩M 引起的转角为θ，剪力Q 引起的转角为γ，由于剪力的影响，矩形微元变成了平行四边形，但横截面没有发生转动。则微元在弯矩与剪力共同作用下的转角
、弯矩、剪力与θ之间的关系可以表示为
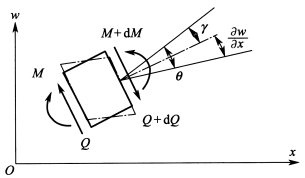
图4-11 剪切和转动惯量的影响
式中：A 是横截面积，G 是剪切弹性模量（Shear Modulus），k 称为铁摩辛剪切系数，其值取决于横截面的形状，对于矩形截面k=5/6，圆形截面k=9/10。
微元d x的运动方程包括平动和转动两个方程。设梁的单位长的转动惯量为J，由动力学定律可得(www.xing528.com)
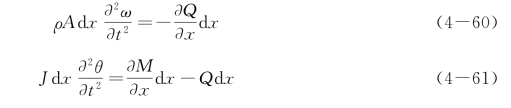
将式（4-58）、式（4-59）代入式（4-60）和式（4-61）得到
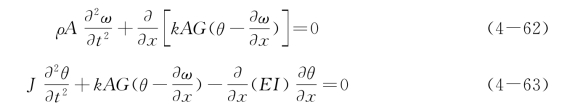
对于均质等截面梁，从方程式（4-62）和方程式（4-63）中消去θ得到
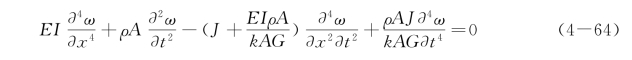
这就是均质等截面梁考虑剪切变形与转动惯量影响时的自由振动方程。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
