自由振动解析优化——探析自由振动

令方程式（4-40）右端的干扰力等于零，得到梁的自由振动方程

假定有分离变量形式的解存在

q（t）的解为式q（t）=D1cosωt+D2sinωt或式q（t）=D sin（ωt+φ），式中D1、D2、D、φ由初始条件确定。于是式（4-46）可表示为

上式代入方程（4-45），便得到特征方程

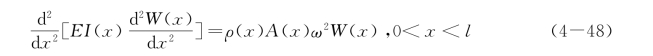
特征式方程（4-48）是变系数微分方程，除了少数特殊情形外，一般不能得到封闭形式的解，只能用近似方法去计算。对于均匀梁的振动，方程式（4-45）简化为

其中

方程式（4-48）简化为

其中式（4-51）是四阶常系数线性常微分方程，设W=eλx代入方程式（4-51）后得到

作为待定参数λ 的四次代数方程，它有四个根，对应于方程（4-51）的四个独立特解为

eβx，e-βx，eiβx，e-iβx，它们构成方程的基础解系。为了应用方便，我们采用另一组等价的基础解系sinβx，cosβx，sinhβx，coshβx，因此方程（4-51）的通解可表示为(www.xing528.com)

其中：Ci（i=1，2，3，4）为积分常数。由于特征方程与边界条件均是齐次的，特征函数包含一个任意常数因子，用四个边界条件只能确定四个积分常数之间的比值，但能导出频率方程，从而确定系统的固有频率。

【例3】求简支梁横向振动的固有频率与固有振型。

【解】由式（4-42）得到边界条件

以通解式（4-54）代入得到C2=C3=C4=0，及频率方程sinβl=0，频率方程的正根为，代入式（4-52）可得固有频率

固有振型

从式（4-56）可以看出，第i阶固有振型有i-1个节点，节点的坐标为

从式（4-57）易知，两相邻节点间的距离（半波长）等于，随着阶数的增高，半波长越来越小。因此，对于高阶固有振动，固有频率的表达式（4-55）必须用更精确的理论加以修正。

表4-5和表4-6列出了几种边界条件下梁的频率方程、振型函数和振型曲线。需要说明的是，振型函数可以是不同的表达形式。

表4-5 几种不同边界条件下梁横向振动的频率方程

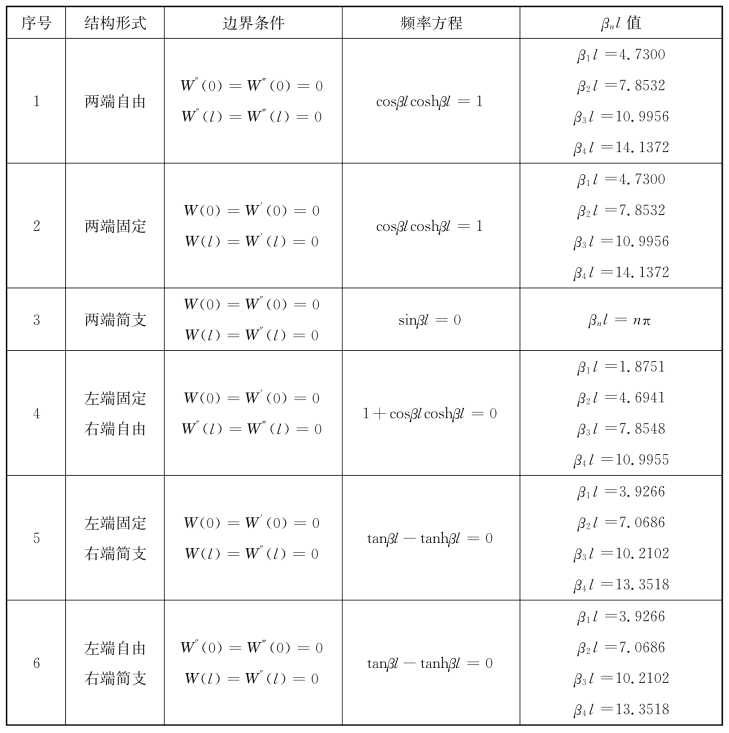
表4-6 几种不同边界条件下梁横向振动的振型函数和主振型

续表