4.3.2.1 振动微分方程
一根圆形横截面的细长直杆,杆的单位体积质量为ρ,截面抗扭刚度为GJt(x),G 为剪切弹性模量,It(x)为截面抗扭常数,对于圆形截面It(x)=Ip(x),Ip(x)为截面的极惯性矩,设杆在扭转振动时截面的翘曲可忽略不计,且始终保持截面平面绕x 轴做微摆动,以φ(x,t)表示距原点x 距离处截面的角位移,现在杆上取一微段dx,其受力如图4-8(b)所示。由材料力学知


图4-8
再根据动量矩定理有

整理后得

把式(4-33)代入上式,得

对于等直杆It为一常数,上式可化简为

式中: ,对于圆截面杆,It=Ip,则c2=G/ρ,c为剪切弹性波沿x 轴的传播速度。
,对于圆截面杆,It=Ip,则c2=G/ρ,c为剪切弹性波沿x 轴的传播速度。
4.3.2.2 杆的扭转自由振动微分方程的解
式(4-34)与式(4-25)具有相同的形式,也是一维波动方程,故其解可直接写成
 (https://www.xing528.com)
(https://www.xing528.com)
式中:A、B、ω、φ 四个待定常数,同前所述,可由初始条件和边界条件来确定。
现把一些常用的边界条件列入表4-3中。
表4-3 常用的边界条件

续表

注:Jp、J0分别为杆的单位长度的质量对x 轴的转动惯量和圆盘质量对x 轴的转动惯量。
同杆的纵向振动一样处理,杆的扭转自由振动的通解由各主振型叠加而成,即

当给定初始条件![]() 后,则由
后,则由

来决定式(4-36)中的常数项An(或Bn)和αn。从前两节中所述的一样,在求解这些常数项时还要应用正交性的关系。
由于杆的扭转受迫振动微分方程应与式(4-32)有相同的形式,为此,其解也有相同的形式。
现以表4-4给出弦、杆及轴振动方程的参数对应关系。由表中对应关系,即可举一反三。
表4-4 弦、杆、轴振动方程参数对照表

例如,已知两端固定的均匀弦的固有频率 及正则振型的表达式Y(x)=
及正则振型的表达式Y(x)= ,…,根据表4-4的对应关系,即可知两端固定的均匀轴的固有频率及正则振型的表达式:
,…,根据表4-4的对应关系,即可知两端固定的均匀轴的固有频率及正则振型的表达式: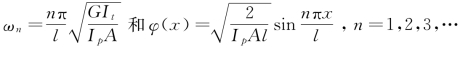 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




