在大型建筑(高层建筑、桥梁、海上采油平台、核电站等)工程中,往往大量采用桩基础。为了确定桩的承载力以及检验工程桩的施工质量,皆要对桩进行动(静)载试验测定。其中动力试验桩法所涉及的基本理论就有杆的纵向振动。对空间结构(桁架中的各杆和机械中的轴类零件)中的构件,其变形皆不可能为单一的沿杆轴线的变形,同时还会产生弯曲变形和扭转变形。在动载荷作用下,空间结构的构件将会发生杆的纵向、弯曲和扭转振动的耦合振动,故连续系统中杆的纵向振动仅是一种基本形式的振动,同理,杆的扭转振动和杆的横向弯曲(即梁的横向弯曲)振动分别也是一种基本形式的振动。本节先介绍杆的纵向振动,再介绍杆的扭转振动。
4.3.1.1 杆的纵向自由振动微分方程
只考虑细长杆的纵向振动,且假设垂直于杆轴线的任一横截面始终保持为平面,该平面仍垂直于杆的轴线,同时,每一横截面内各质点只沿着杆轴线方向做相等位移,即不计入杆的横向变形。
以连续系统为力学模型来建立振动微分方程。
如图4-3(a)所示的杆其截面抗拉刚度为EA(x),E 为弹性模量,A(x)为横截面面积,杆的单位体积质量为ρ。两端自由,在沿轴向的外干扰力移去后,发生沿杆的纵向振动。
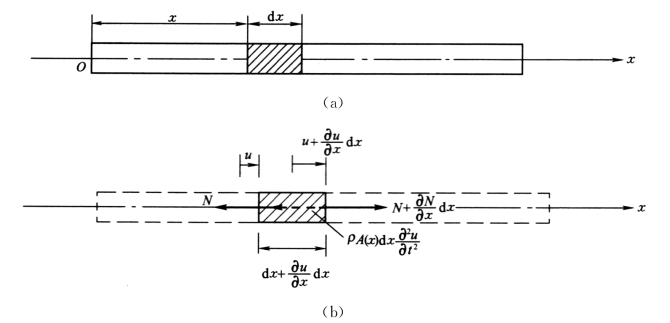
图4-3
设u(x,t)为t时刻,离坐标原点x 处的横截面的纵向位移,即它是横截面的位置和时间t的二元函数。现从杆中取一微段dx来进行研究,其受力如图4-3(b)所示。设N 为在x 处横截面上的轴力,且规定其使杆发生拉伸变形时为正,则在x+dx处横截面上的轴力应为
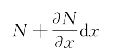
同时,在该处的位移为
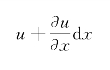
故轴向应变量为
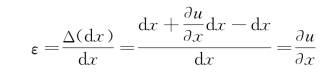
根据胡克定律,有σx=Eεx。又根据杆受轴向力作用时的应力计算公式![]() ,为此有
,为此有
![]()
根据动静法,应在微段上虚加惯性力![]() (略去二阶微量
(略去二阶微量![]() ),得
),得
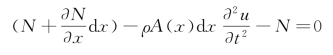
整理后,有
把式(4-23)代入上式得
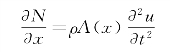
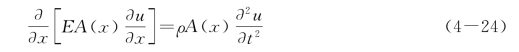
当A(x)为常量时,即杆为等直杆时,式(4-24)可写为

式中: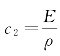 ,c为弹性纵波沿杆轴线的传播速度(这个速度为材料内声的速率)。
,c为弹性纵波沿杆轴线的传播速度(这个速度为材料内声的速率)。
4.3.1.2 杆的纵向自由振动微分方程的解
式(4-25)是一维波动方程。求此方程的解同前所述,用类似的分离变量的方法,设其解为u(x,t)=U(x)T(t),可得

解这两方程,可得出其解为
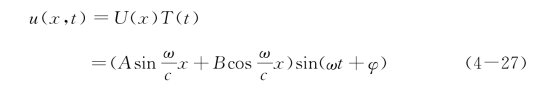
式中:A、B、ω、φ 四个待定常数,可由初始条件和边界条件来决定。
例如杆的两端为固定端时,其边界条件为
u(0,t)=0,u(l,t)=0
将它们代入式(4-27)可得
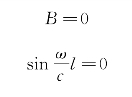
从而得出
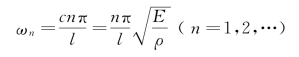
对应的主振型为
![]()
又如杆的两端为自由端时,其边界条件为
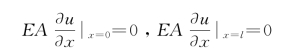
即在自由端处轴向力为零。对式(4-27)求导,得
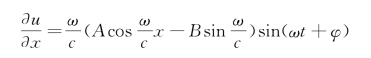
再把初始条件代入上式,即有
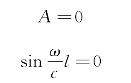
则有
![]()
取n=0,1,2,…,即可得到纵向振动时各种不同类型的频率。它与两端固定的杆不同之处是存在着一个n=0时的固有频率ωn=0,其含义为杆顺轴线方向做刚体平移。对应的主振型为
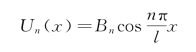
对应于零频率,即ω0=0时,若取B0=1,则其主振型为
Un(x)=1
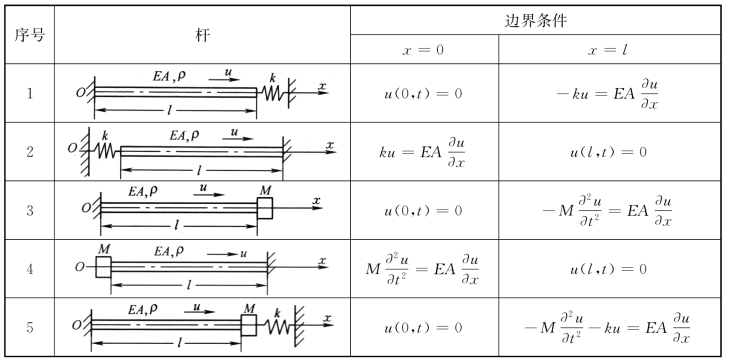
由于各种边界条件组合繁多,在此不再一一推导,在表4-1中列出三种边界条件下的杆纵向振动频率方程、固有频率及主振型。在表4-2中仅列出其他情况的边界条件。
表4-1 三种情况的边界条件

续表
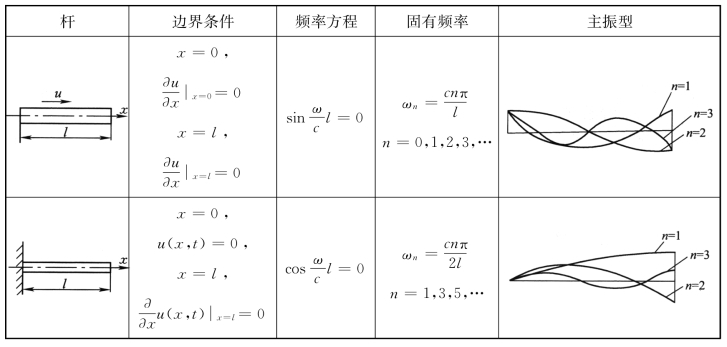
表4-2 其他情况下的边界条件
同弦的自由振动一样处理,杆的纵向振动的通解也是由无限多阶主振型的叠加而得到的,如对两端固定的杆有
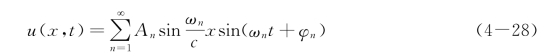
或
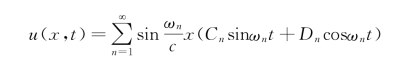
式中:An、φn 或Cn、Dn两个待定常数,可根据初始条件来决定。
【例1】图4-4中所示一等直杆的横截面面积为A,单位体积的质量为ρ,弹性模量为E,长度为l,其左端被固定,而右端固结一质量为M 的质量块,试计算其固有频率及进行正交性条件的推导。
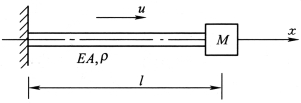
图4-4
【解】(1)计算固有频率。
根据式(4-27),有
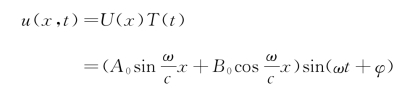
现在右端固结一质量块,则在振动过程中,它对杆端有一惯性力,故边界条件为
代入式(4-27),得
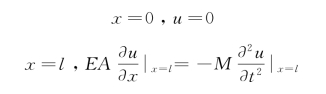
B0=0
及
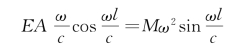
把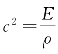 代入上式,整理后得
代入上式,整理后得

式中:![]() 为杆的质量和附加质量块的质量之比。式(a)为频率方程,也为超越方程。欲求此方程的根,除应用电算法之外,尚可应用作图法求解。现设
为杆的质量和附加质量块的质量之比。式(a)为频率方程,也为超越方程。欲求此方程的根,除应用电算法之外,尚可应用作图法求解。现设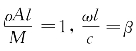 ,则式(a)可写为
,则式(a)可写为
![]()
然后,分别画出tanβ和1/β的曲线图形,如图4-5所示。根据此两根曲线的各个交点β1,β2,…,可求得各阶固有频率。现求头两阶的固有频率,由图4-5可量得β1=0.86,β2=3.43,则可求得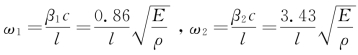 。
。
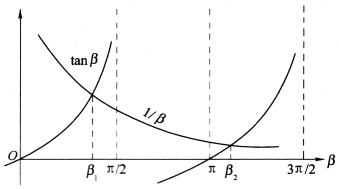
图4-5
【讨论】①当杆的质量和附加质量块的质量之比不为1时,令v 为质量比,由式(a)有
v=ρAl/M,ωl/c=β
则式(a)可简化为
![]()
应用式(c),当给定质量比的一个数值时,应用数值解法就可求出一系列的β 值,再代入ωl/c=β中,可求得
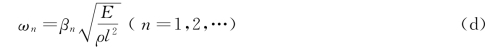
即可求出各阶的固有频率。
②当杆的质量比v 在两种极端情况,即v ≈∞和v ≈0时。
a.当v ≈∞时,由式(c)知tanβ=∞,即
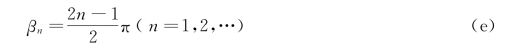
将式(e)代入式(d),得
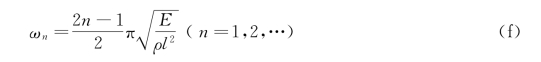 (https://www.xing528.com)
(https://www.xing528.com)
与表4-1中的一端固定一端自由的杆件固有频率相同,说明此时质量块M 的作用可以忽略不计。
b.当v ≈0时,由式(c)知,tanβ很小,故有tanβ≈β,代入式(c),得
![]()
将v=ρAl/M 和ωl/c=β代入上式,得

因![]() 是杆的纵向刚度,说明式(h)即为略去杆的分布质量后,得到的单自由度系统的固有频率。
是杆的纵向刚度,说明式(h)即为略去杆的分布质量后,得到的单自由度系统的固有频率。
值得注意的是,若v=0.1时,由数值计算可得β1=0.32,将此值代入式(d)中,得

若v=0.1,代入式v=ρAl/M 中,则M=10ρAl,再代入式(h)中,则
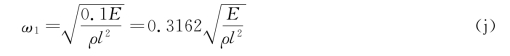
式(j)与式(i)比较,相对误差仅为1.18%。
为此,当v 值较小时,略去杆的质量,可得到精度较好的结果。
(2)正交性条件的推导。
当杆的支承不为固定端、自由端时,杆的两个不同阶主振型Yn、Ym之间的正交性表达式如下
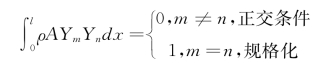
现本例中在杆的右端有一质量块,这种情况与上述的情况不相同,为此,必须重新证明在端点处带有一质量块的杆的两个不同阶主振型之间的正交性。
设Un(x)和Um(x)分别为n 阶和m 阶固有频率ωn和ωm的两个不同的主振型函数,它们必须满足方程
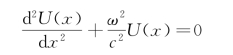
式中:c2=E/ρ,现重新整理上式后,得
![]()
式中:m=ρA,分别把Un(x)和Um(x)代入式(a),即得
![]()
用Um和Un分别乘式(b)和式(c),并对整个式子积分可得
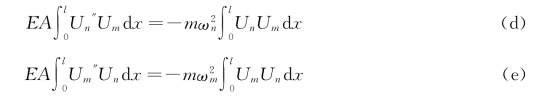
现对式(d)和式(c)分别应用分部积分法,可得
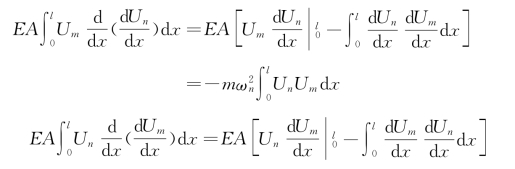
![]()
将上两式相减得
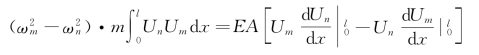
将边界条件
代入式(f)得
![]()
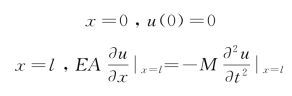
故有
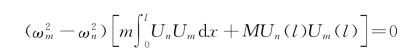
当m ≠n 时,![]() ,则有
,则有
![]()
这就是在端点处带一质量块的杆的纵向振动的主振型对于质量的正交性条件。该式与在端点处无质量块的杆的纵向振动的主振型对质量的正交性条件相比较,多了一项附加项MUn(l)Um(l)。当m=n 时,![]() ,则有
,则有
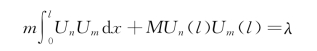
式中:λ是一个任意常数。若取λ=1,则振型函数即可按照下面方式规格化
![]()
4.3.1.3 杆的纵向强迫振动微分方程的解
在两端自由的杆上作用着匀布的轴向力Q(x,t),如图4-6所示。设截面抗拉刚度为EA(x),E 为弹性模量,A(x)为横截面面积,杆的单位体积质量为ρ。在这种情况下,杆的运动微分方程为
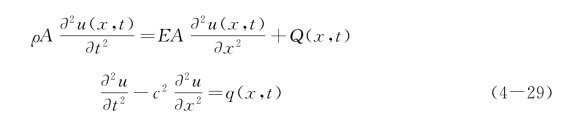
![]()
图4-6
式中:q(x,t)=Q(x,t)/ρA。方程(4-29)为一非齐次方程,求解时可仍用振型函数Un(x),若杆的边界条件为两端固定时,其为
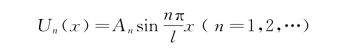
而不同的是杆的振动方式Tn(t)为未知的时间函数。由于确定振型函数时,必须满足边界条件,故振型函数与未知的时间函数的乘积为
![]()
上式也必须满足边界条件。又因非齐次方程式(4-29)的解也应满足边界条件,故可假设方程式(4-29)的解为
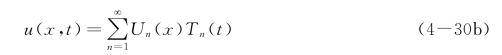
把式(4-30b)代入式(4-29)中后,再应用正交性条件和规格化后,可得
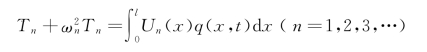
式中:Un(x)是正则振型函数,则该方程即为n 阶正则振型方程。根据杜哈美积分求得
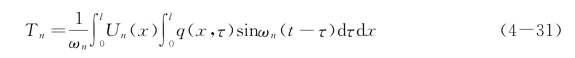
将此时间函数代入方程式(4-30b)中,可得出杆的纵向强迫振动的响应为
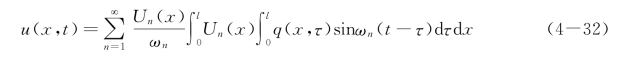
【例2】如图4-7(a)所示为一端自由,另一端固定端的细长杆。已知其固定端支承相对于地面的运动按抛物线函数
ug=u0(t/t0)2
做平移。设杆的长度为l,杆的截面抗拉刚度为EA,E 为弹性模量,A 为横截面面积,ρ为杆的单位体积质量。在初瞬时,杆处于静止。试确定支承运动所引起的杆的纵向振动的响应。

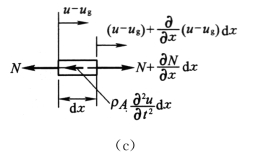
图4-7
【解】设u(x,t)为t时刻,离坐标原点为x 处的横截面的纵向位移。现从杆中离x 处取一微段d x,其受力如图4-7(b)所示。
由材料力学知轴向应变为
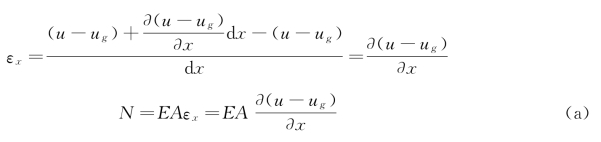
根据动静法得
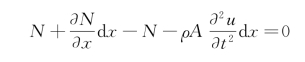
整理后得

把式(a)代入式(b)中,可得
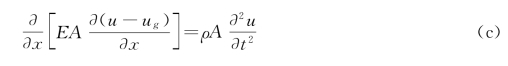
设
u*=u-ug
则有
![]()
现把此两式代入式(c)中,得
![]()
令c2=E/ρ,并代入上式,且整理得

再令![]() ,代入上式
,代入上式

式(e)和式(4-29)相同。现先解齐次方程
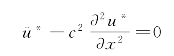
根据边界条件,最后得到固有频率为
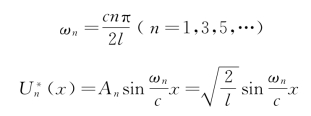
式中:![]() 已是规格化的正则振型函数,根据式(4-32)有
已是规格化的正则振型函数,根据式(4-32)有
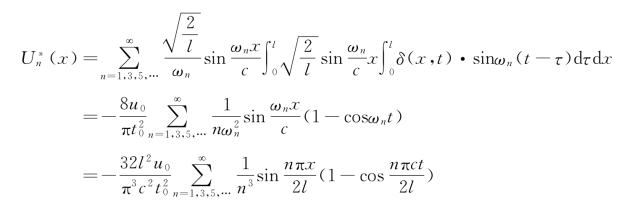
由支承运动引起的杆纵向振动的响应为
u=u*+ug
故
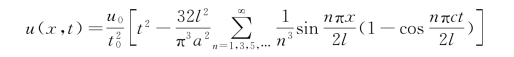
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




