弦的振动方程

如图4-1（a）所示为一两端固定、用张力T 拉紧的弦，在初始激励下做横向自由振动。现将弦任意分成n+1段，每段弦的质量分成两半缩聚到每段的两端。以mi（i=1，2，…，n）表示各点质量，各质量mi之间为无质量、具有张力T 的弦段所连接，成为n 自由度系统（在两端的两个质量m0和mn+1不振动）。

图4-1

以yi（i=1，2，…，n）表示各mi偏离平衡位置的位移。由于是微振动，各质点的位移很小，弦伸长引起的张力变化可忽略不计，即在整个振动过程中T 保持不变。但因相邻两段弦中张力的方向不同，所以在mi上将受到T 的不平衡垂直分力的作用，如图4-1（b）所示。对mi质点列出∑Y=0

或写为

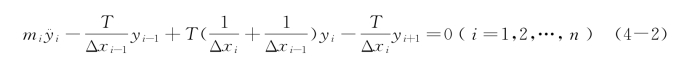
若令，则式（4-2）成为

这就是以刚度系数表达的n 个二阶常微分方程组，写成矩阵形式为

再回到式（4-1），如记Δyi=yi+1-yi，Δyi-1=yi-yi-1，则此式可写成

式（4-4）两边除以Δxi，则(www.xing528.com)

如将分段无限缩小，即Δxi→0，质量就分布在弦的全长。以ρ表示弦单位长度的质量，y 是x 和t的二元函数，上式趋向它的极限，即得到弦振动的偏微分方程为

此式也很容易用如图4-2（a）所示的连续系统模型直接导出。建立如图4-2（a）所示坐标系，在弦上取x处一微段d x，其质量为d m=ρd x。在任一瞬时微段两端作用着大小相等但方向不同的张力T，如图4-2（b）所示。在微幅振动假设下，，d s=d x，列出∑Y=0，得

图4-2

再代入，化简，得

可见从两个不同的模型出发可以得到相同的结果，它们之间并无本质区别。

令，它具有速度的量纲，表示弹性波沿弦长度方向的传播速度，则式（4-6）成为

上式通常称为波动方程。