阻尼对强迫振动的影响分析

前面为了简化问题，并突出两自由度系统振动的基本特性，在讨论过程中，没有考虑阻尼。实际上系统总是有阻尼的。为了简单而又易于说明问题，下面我们以图3-17所示的两自由度系统为例说明阻尼对强迫振动的影响。

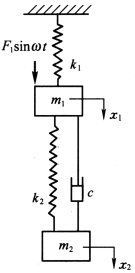
图3-17

这个系统是在动力减振器的两个质量块之间加上一个阻尼器而组成的，称为阻尼减振器。系统的运动微分方程为

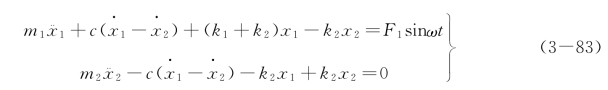
这个有阻尼的两自由度系统的振动微分方程只要在式（3-77）的左边都加上一项阻尼力就可以了。但它的解却要复杂得多。我们用复数解上述耦合的联立微分方程，以F1eiωt表示式（3-83）第一式右边的激振力。正如单自由度系统那样，两自由度系统的稳态响应也一定是与激振力同频率的，但因阻尼而使响应落后于激振力一相位角。设其解具有如下形式

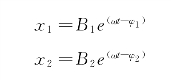
代入式（3-83），得

从以上两式可解出B1、B2。为了讨论阻尼对主质量m1强迫振动的影响，这里计算B1。

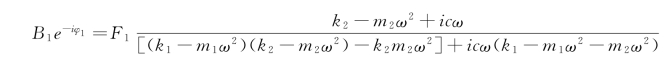
根据复数运算规则有

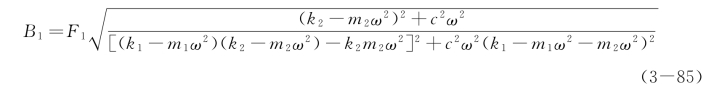
令

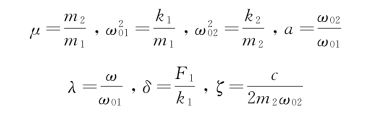(https://www.xing528.com)

则式（3-85）可写成无量纲形式

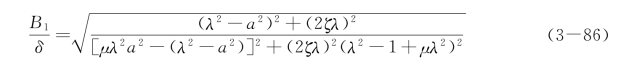
可见振幅B1是4个参数μ、a、ζ、λ的函数。μ、a 是已知的，B1/δ 即为ζ 和λ 的函数，这和单自由度系统的强迫振动情况一样。

图3-18表示μ=1/20，a=1的阻尼减振器，在不同的阻尼ζ下，主质量振幅的动力放大系数B1/δ随频率比λ=ω/ω01变化的幅频响应曲线。

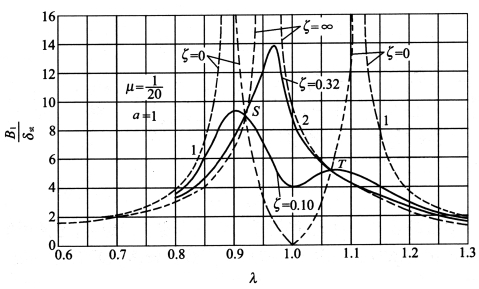
图3-18

当ζ=0，即为无阻尼强迫振动情况，式（3-86）变为

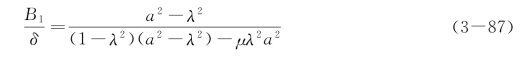
其幅频响应曲线如图3-18中虚线所示。当λ=0.895，λ=1.2时为两个共振频率。

当ζ=∞时，两质量块m1与m2之间无相对运动，系数变为只有一个质量块m1+m2和弹簧刚度k1的单自由度系统。由式（3-86）得

其幅频响应曲线与无阻尼单自由度强迫振动的相同，如图3-17中曲线所示。令式（3-88）的分母等于零，可得共振时的频率比为

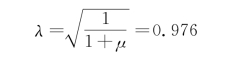
图3-17中画出了ζ=0.1和ζ=0.32的两条响应曲线，表明阻尼使共振附近的振幅显著减小，而且在相同的阻尼下，频率高的那个共振振幅降低的程度比频率低的那个大，这就是为什么实际结构的动力响应只需考虑最低n 阶振型的原因。

从图3-17中还可看出，在激振频率ω≪ω1或ω≫ω2的范围内，阻尼的影响是很小的，且所有的响应曲线都通过S和T 两点。这意味着对于这两个相应的λ值，质量块m1的强迫振动振幅与阻尼大小无关。这对于设计阻尼减振器时选择最佳阻尼比ζ 和最佳频率比λ 是必要的。