无阻尼系统的强迫振动优化措施

对于无阻尼系统的强迫振动的一般性质，仍按如图3-12所示的双弹簧—质量系统为例进行讨论。

如图3-16所示，设两质量块分别在简谐激振力F1sinωt和F2sinωt作用下运动。根据牛顿运动定律，可直接写出系统强迫振动的微分方程

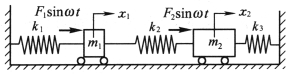
图3-16

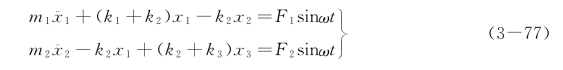
令

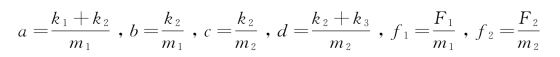
于是式（3-77）写为

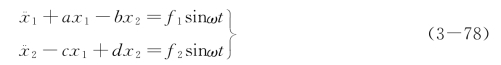
这是二阶线性常系数非齐次微分方程组。其齐次方程解即为前面讨论过的自由振动，由于阻尼的存在，在一段时间以后自由振动就逐渐衰减掉。非齐次的特解则是稳定阶段的等幅振动，系统按与激振力相同的频率ω 做强迫振动。设其解为

式中：振幅B1、B2为待定常数，代入式（3-78），有

则方程的系数行列式为(www.xing528.com)

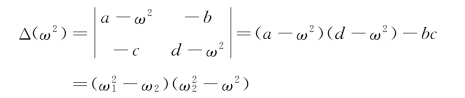
式中：ω1、ω2为系统的两个固有频率。解方程式（3-80），有

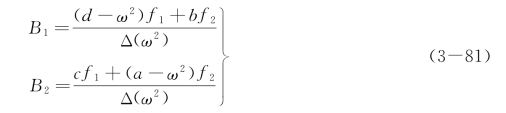
将B1、B2代入式（3-79）即为系统在激振力作用下的稳态响应，是与激振力的频率相同的简谐振动。其振幅不仅取决于激振力的幅值F1与F2，特别与系统的固有频率和激振频率之比有较大关系。由式（3-81）可见，当激振频率ω 等于ω1或ω2时，系统振幅无限增大，即为共振。两自由度系统的强迫振动有两个共振频率。

同时由式（3-81）可知，两个质量块的振幅比为

式（3-82）说明，在一定激振力的幅值和频率下，振幅比是定值，也就是说系统具有一定的振型。当激振频率等于第一阶固有频率ω1时，振幅比为

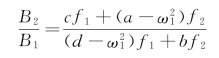
由式（3-69）中可求出μ1、μ2。现对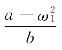的分子分母均乘以的分子分母均乘以f1，然后按比例式相加法则可得

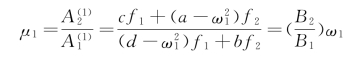
同理

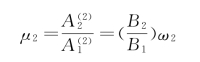
这表明系统在任意一个共振频率下的振型就是相应的主振型。在实践中经常用共振法测定系统的固有频率，并根据测出的振型来判定固有频率的阶次。其振幅频率响应曲线同单自由度强迫振动一样，可用频率比作为横坐标，振幅作为纵坐标画出。