耦合与主坐标的关系

一般情况下两自由度系统振动微分方程组如式（3-63）所示，每个方程式中往往都有耦合项。这种坐标x1和x2之间有耦合的情况称为静力耦合或弹性耦合。

在例9中，若以弹簧支承处的位移x1与x2为独立坐标来建立振动微分方程，见图3-13，x1、x2与x、θ关系如下

x1=x+l1θ，x2=x-l2θ

转换后得

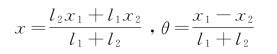
将上式代入刚体平面运动微分方程

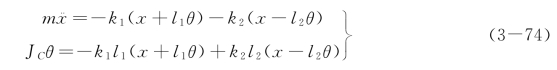
有

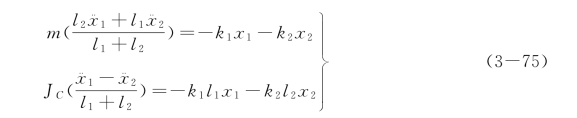
整理得

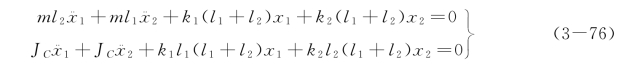
上面的方程中不仅坐标x1和x2有耦合，而且加速度和的项也有耦合，这种加速度之间有耦合的情况，称为动力耦合或惯性耦合。式（3-76）同时具有静力耦合和动力耦合，属于耦合的一般情况。如果选取的坐标恰好可使微分方程组的耦合项全等于零，既无静力耦合，又无动力耦合，就相当于两个单自由度系统，这时的坐标就称为主坐标。选取不同的独立坐标所建立的运动微分方程形式虽然不同，但坐标的转换并不影响固有频率的计算结果。如果一开始就用主坐标建立微分方程，那么固有频率的计算就变得很简单了，但问题是，一开始不容易直接找到这种主坐标。

在例9中，是以x 与θ为两个独立坐标。如果k1l1=k2l2，则引入的符号b=c=0，则式（3-63）中的耦合项均为零，简化成

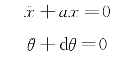
相当于两个单自由度系统各自独立地做不同固有频率的主振动(www.xing528.com)

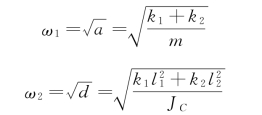
这时所选的坐标x 与θ就是主坐标。

【例10】用刚度影响系数法，建立如图3-15所示的两自由度系统的运动微分方程。

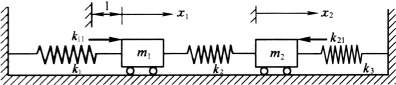
图3-15

解：首先用力使质量块m1，从静平衡位置移动一单位位移，同时用力制住m2不动。这时对m1沿x1正方向施加的是弹簧k1和k2的弹力之和。因位移为1，因此弹力之和为k1+k2，即k11=k1+k2，这时在质量块m2上施加的力的大小等于k2，方向与x1位移方向相反，即k21=-k2。再用力使质量块m2离开静平衡位置单位位移，同时用力制住m1不动，得k22=k2+k3，k12=-k2。将所得的刚度影响系数代入用刚度系数建立的振动微分方程组，有

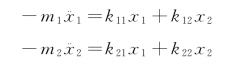
移项整理得

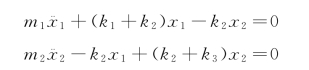
上式即为式（3-62）。此式可用矩阵形式表示

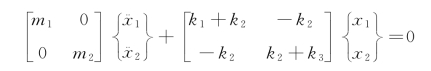
或

式中：x、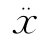分别是系统位移、加速度列阵，M、K 分别是系统的质量矩阵和刚度矩阵。从刚度矩阵可知，刚度影响系数kij为刚度矩阵K 中的一个元素。