固有频率和振型分析

对于无阻尼自由振动系统，可以根据多自由度系统作用力方程的一般形式变为

假设方程的解

这里：为与各广义坐标对应的与时间无关的向量，ω 为固有频率，φ 为初相位。

将式（3-20）代入式（3-19）得

与线性代数中的特征值问题相对照，我们把式（3-21）称为广义特征值问题。要使式（3-21）有解，必须使其系数行列式为零，即

上式称为特征方程（Characteristic Equation）。由此可求出n 个非负的特征根1，2，…，n），将每个特征根代入式（3-21）即可得到相应的非零向量显然有

上式为n 个为未知数的齐次代数方程。对于一个特定的，式

（3-23）只能确定出与对应的各个分量的比例。

由式（3-22）和式（3-23）看出，ωi和只决定于系统本身的物理特性，而与外部激励和初始条件无关，这表明它们都是系统的固有属性。ωi称为系统的固有频率，按从小到大的顺序排列，即）称为系统的固有振型（Natural Mode Shape）或主振型（Principal Mode Shape）（或称特征向量、固有向量、模态向量等）。

式（3-20）表明振动系统各个质量按相同的频率和相位角做简谐运动，这种运动称为固有振动（Natural Mode of Vibration）或主振动（Principal Mode of Vibration）。系统在主振动中，各质点同时达到平衡位置或最大位移，而在整个振动过程中，各质点位移的比值将始终保持不变，也就是说，在主振动中，系统振动的形式保持不变，这就是振型的物理意义。每一个主振动称为一个模态，ωi和对应的组成第i阶模态的参数。

由式（3-21）和式（3-22）可知，固有振型具有一个未确定的常数因子，通常假设振型的某个元素为1，则其他元素就可以表示为此元素的倍数，这种方法或过程称为振型的基准化（Benchmark of the Vibration Mode），一般假设振型的第一个元素为1。

固有振型除了通过广义特征值问题式（3-23）求解以外，还可以通过求伴随矩阵的方法求解。定义特征矩阵（Eigenmatrix）

利用数学的概念知

这里：为逆矩阵，为伴随矩阵，为单位矩阵。

由式（3-22）知，因此

比较式（3-23）和式（3-26）知，伴随矩阵的每一个非零的列都与成比例，则构成固有振型。(https://www.xing528.com)

对于位移形式的无阻尼自由振动方程

引入记号

称为动力矩阵（Dynamic Matrix）。将式（3-20）代入方程（3-27）得到

特征方程为

上式有n 个正实根，系统的固有频率为

与λi对应的振型可通过式（3-29）求得。类似地，固有振型也可以通过求的伴随矩阵得到。

【例8】跨度为l的简支梁，弯曲刚度为EI，梁上有三个相同的集中质量，如图3-9所示，忽略梁质量对系统固有频率的影响。求固有频率和固有振型，并画出振型图。

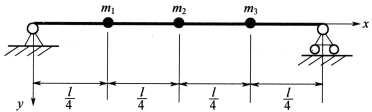
图3-9 梁的振动

解：取三个集中质量的横向位移y1、y2和y3为广义坐标。

动能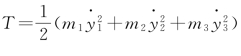，则质量阵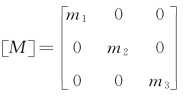，现求柔度影响系数，注意到Rij=Rji，且由所给条件的对称性，有R11=R33，R12=R32。设在m1处作用单位力1，由材料力学公式可以求得

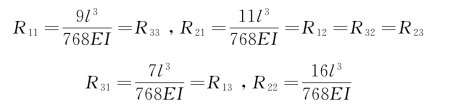
因此，柔度矩阵为，位移形式的振动方程为

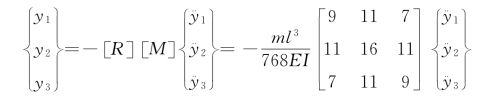
将质量矩阵［M］和柔度矩阵［R］代入特征方程式（3-30）得

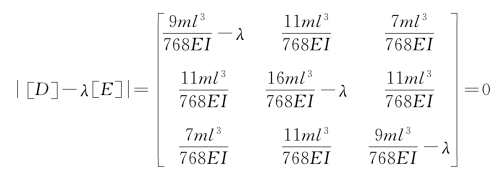
展开上式可求出三个固有频率为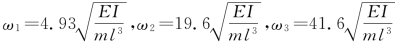；将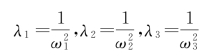分别代入式（3-29），并设，即可求出三个固有振型。三个振型对应的梁的挠度曲线如图3-10所示。

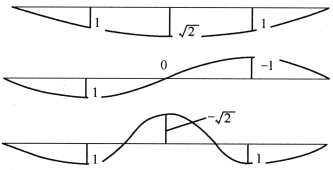
图3-10 振型图