牛顿第二定律（或达朗伯原理）的解释和应用

【例1】图3-1是一个双质量弹簧系统，质量m1与m2用刚度分别为k1、k2及k3的三个弹簧联结于支撑，两个质量只做水平方向的运动，并分别受到激振力P1（t）及P2（t）的作用，不计摩擦和其他形式的阻尼，试建立系统的运动微分方程。

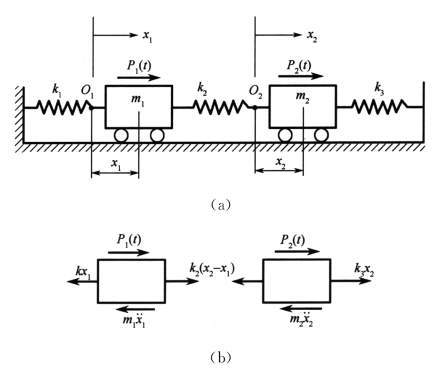
图3-1 双质量弹簧系统

解：这是一个两自由度的系统，可以用原点分别取在m1和m2的静平衡位置上的两个坐标x1和x2来描述系统的运动。设某一瞬时质量m1和m2分别有位移x1和x2，加速度和及，由隔离体受力分析和达朗伯尔原理得到下列两个方程

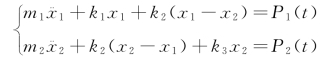
经整理，得

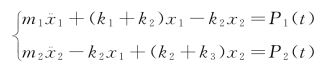
上面的方程组即系统的运动微分方程，方程中每一项都是力的量纲，上述方程组可以用矩阵表示为

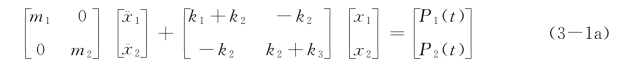
或

式中：

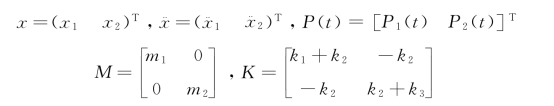(www.xing528.com)

【例2】安装在两端固定的轴上的两个圆盘在外力偶矩M1（t）、M2（t）的作用下做扭转振动，如图3-2所示。已知两个圆盘的转动惯量分别为I1、I2，轴的三个区段的扭转刚度分别为及，试建立系统的运动微分方程。

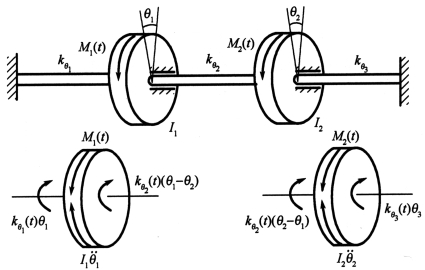
图3-2

解：这个扭转振动系统用角坐标θ1、θ2描述，设某一瞬时圆盘I1与I2分别有角位移θ1及θ2，角加速度θ¨1及θ¨2，由受力分析和达朗伯原理，得到运动微分方程为

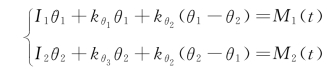
上式的矩阵形式为

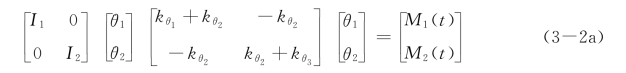
或

式中：

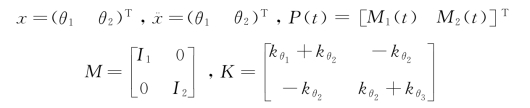
例1与例2比较可知，多自由度系统的扭转振动与直线振动在数学描述上相同。如同在单自由度系统中做过的那样，在多自由度系统中也将质量、刚度、位移、加速度及力都理解为广义的。