2.6.3系统在不同激励力下的响应特性分析与优化

在如图2-34所示的系统中，作用有一任意激励力F（t）。设n ＜ωn为欠阻尼情形。

仍采用前几节的符号规定，则得物块的运动微分方程

图2-36表示任意激励力F（t）的图形。当系统受到这种激励力的作用时，可以将激励力F（t）看作是一系列冲量的叠加。对于在时刻t=τ 的元冲量为，由式（2-68），得到系统对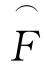的响应为

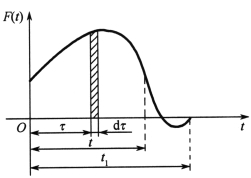
图2-36

由线性系统的叠加原理，系统对任意激励力的响应等于系统在时间区间0≤τ≤t内各个元冲量的总和，即

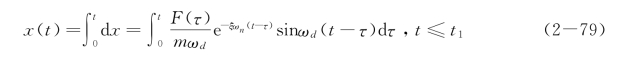
对无阻尼的振动系统，可令式（2-79）中的ξ=0，得到任意激励力的响应为

将单位脉冲函数响应的表达式（2-77）与式（2-79）、式（2-80）比较，可得到单自由度系统对任意激励力响应的统一表达式

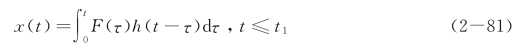
式（2-81）的积分形式称为卷积。因此，线性系统对任意激励力的响应等于脉冲响应与激励的卷积。这个结论称为博雷尔（Borel）定理，也称杜哈梅（Duhamael）积分。

如果系统有初始位移x0和初始速度，则单自由度黏性阻尼系统对任意激励力的响应为

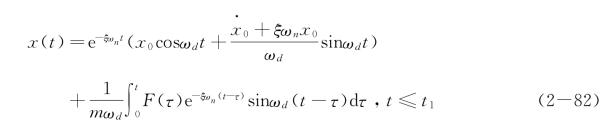(www.xing528.com)

无阻尼振动系统的响应为

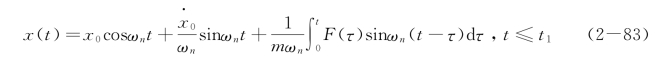
应该注意，以上讨论的是物块在激励力作用的时间区间以内的运动。t＞t1，即激励力停止作用后，物块的运动称为剩余运动。此时单自由度黏性阻尼系统对任意激励力的响应可在式（2-79）、式（2-80）中将t1作为积分上限直接求得，即

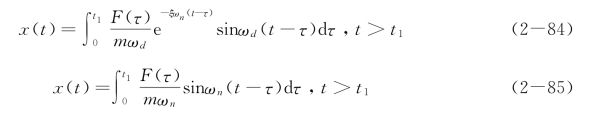
也可以x（t1）和为初始条件，利用式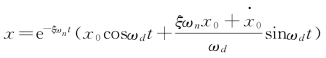来求得，即

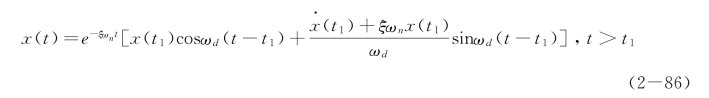
【例8】无阻尼弹簧—质量系统受到突加常力F0的作用，试求其响应。

解：取开始加力的瞬时为t=0，突加常力F0可表示为如图2-37所示阶跃函数载荷。设物块处于平衡位置，且，将F（τ）=F0代入式（2-80），积分后得响应为

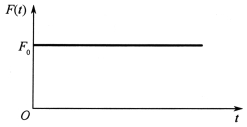
图2-37

可以看到，在突加常力作用下，物块的运动仍是简谐运动，只是其振动中心沿力F0的方向移动一距离也是F0使弹簧产生的静变形。

若上述阶跃力从t=a 开始作用，如图2-38所示，则系统的响应为

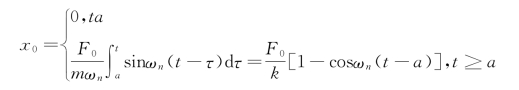
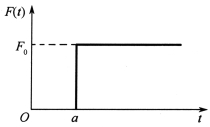
图2-38