小阻尼情况下的自由振动及曲线分析

此时阻尼比ξ＜1，根式为纯虚数，s1，s2为一对共轭复数

令，运动微分方程式（2-35）的通解为

式中：c1，c2为一对共轭复数。

利用欧拉公式，得

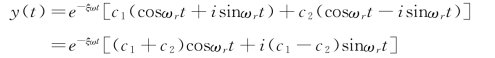
令c1+c2=c3，i（c1-c2）=c4，则c3，c4为实数，运动微分方程的通解成为

速度的表达式为

引入初始条件

则

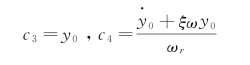
最终得到有阻尼自由振动的解为

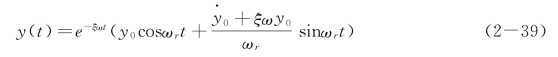
式（2-39）也可写为

(www.xing528.com)

式中

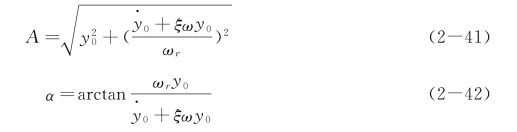
式（2-40）画出曲线如图2-27所示，可见小阻尼情况下自由振动仍有周期性，但已非等振幅的简谐振动，振幅随时间衰减变小，这种衰减自由振动的圆频率为，比无阻尼的圆频率ω 小。

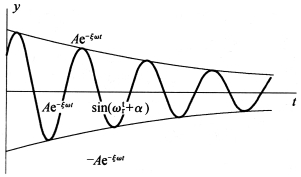
图2-27

结合式（2-40）和图2-27，即可分析阻尼对自由振动的影响。

首先看阻尼对固有频率的影响

因此，阻尼固有频率减小，使固有周期增大。但工程中通常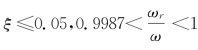，所以阻尼对固有频率（周期）的影响极小。有阻尼频率（周期）可近似地等同于无阻尼频率（周期）

其次看阻尼对振幅的影响。从图2-27可看到，阻尼对振幅的影响很大，阻尼使系统振动的振幅按几何级数衰减，为了定量描述阻尼对振幅的衰减影响程度，把相邻两个振幅之比称为振幅衰减率，即

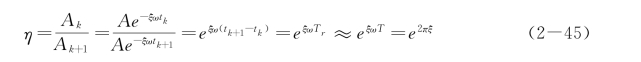
实用上为了避免求指数值的不便，常用对数衰减率来代替振幅衰减率

也可用相隔n 个周期的两个振幅之比表示对数衰减率

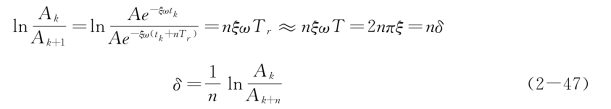
因此

式（2-48）可用于测量阻尼比，只要测出相隔n个周期的两个振幅Ak，Ak+n，即可换算出系统的阻尼比，进一步可换算得到黏性阻尼系数。