如何用动静法求解结构变形问题？

根据达朗贝尔原理，在质量上添加假想惯性力后，一个本质上的动力学问题就变成一个形式上的静力学平衡问题。利用动静法建立振动方程时，又有刚度法和柔度法两种具体形式。

2.1.1.1 刚度法

刚度法首先将质量取出作为隔离体，画出隔离体受到的力，包括实际存在的外荷载、弹性力、阻力、约束反力等，以及引入的假想惯性力；然后描述隔离体受到的力，除外荷载给定之外，将弹性力用位移表示，阻力用速度（位移对时间的一阶导数），惯性力用加速度（位移对时间的二阶导数）表示；最后列出隔离体的平衡方程并化简，对平动自由度一般列力的平衡方程，对转动自由度一般列力矩平衡方程。

由于用刚度系数描述弹性恢复力，对隔离体列出平衡方程，故名刚度法。

【例1】如图2-1（a）所示的光滑水平面上的弹簧质量系统，是最简单的单自由度系统，其他任何单自由度系统都可等价为特定质量和刚度的弹簧质量系统。

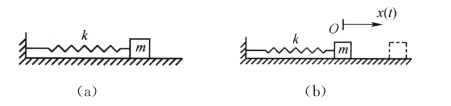
图2-1

在图2-1（b）中的原点O，弹簧为原长，弹簧力为零，这是物体的静平衡位置。当物体从此位置向右偏离时，弹簧受拉，它作用于物体的力水平向左；而当物体从此位置向左偏离时，弹簧受压，它作用于物体的力水平向右。可见弹簧力总是指向原点O，力图使物体回到静平衡位置，这种力称为恢复力。

假定用手把物体从位置O 向右拉至距离x0后使它静止，则在放手后物体将在弹簧力的作用下向左变加速运动；回到位置O 时弹簧力虽变为零，但物体具有速度，由于惯性将继续向左运动，越过O 点后弹簧力使物体减速，直至速度等于零，此后弹簧力又使物体开始向右运动。物体将在平衡位置附近往复运动，在没有阻力的理想条件下，这种运动一经开始将永不停止地进行下去。

解：质量的运动和自由度如图2-1（b）所示，在任一时刻取出质量，画出其水平方向受力图如图2-2所示。

图2-2

弹簧给予的恢复力kx与位移成正比，方向与之相反；惯性力与加速度成正比，若画成与其参考正方向相反，则表示为；若画成与其参考正方向相同，则应表示为。

对两个受力图列出∑X=0，都有

化简，得

若将例1的弹簧质量系统放在竖直方向，质量运动方向有重力，情况如何？

质量的运动和自由度如图2-3所示，由于重力在运动方向，使弹簧产生静变形Δst，静平衡位置与弹簧原长位置不同，分两种情况建立方程并进行比较。

图2-3

情况1：以初始位置为基准，受力图如图2-4所示。

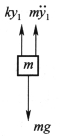
图2-4

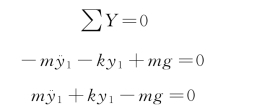
情况2：以静平衡位置为基准，受力图如图2-5所示。

图2-5

注意到kΔst=mg，因此，有

可见若重力在运动方向，以静平衡位置为基准建立运动方程，也就是对动位移建立运动方程，则不受重力的影响。

【例2】如图2-6所示，抗弯刚度无穷大的直杆，两端有两个集中质量。

图2-6

解：尽管有两个集中质量，但此振动系统仅有一个自由度，小幅度转动时质量的运动和自由度如图2-7所示。

将刚性杆连同两个质量取出，受力如图2-8所示。

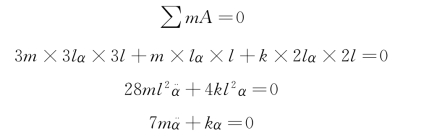
图2-7

图2-8

在有些振动系统中，并没有直接给出弹簧，是由弹性杆件发挥弹簧作用，提供恢复力。

【例3】如图2-9所示的单层单跨剪切型刚架，横梁抗弯刚度无穷大，结构的质量集中在横梁上。

图2-9

解：结构的变形、质量的运动和自由度如图2-10所示，在任一时刻取出质量，画出水平方向受力如图2-11所示。

图2-10

图2-11

两根柱顶剪力即为横梁振动的恢复力，使之向平衡位置运动，令柱的线刚度，根据结构力学的杆端弯矩方程，有

同理

由∑X=0

将式（2-3）和式（2-4）代入，得(www.xing528.com)

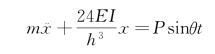
因此，对剪切型钢架，定义柱侧移刚度为其上下端产生单位相对位移时柱中的剪力，即

每根柱相当于一个弹簧，弹簧刚度就是柱侧移刚度。同时定义刚架层间侧移刚度为该层各柱侧移刚度之和∑ki。

【例4】如图2-12所示的简支外伸梁，AB 为弹性杆B，不计质量，BC 为刚性杆，具有均布质量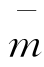。试建立振动微分方程。

解：如图2-13所示，用支座B 处转角α（t）即可描述全部质量的位置，故此系统为单自由度系统。在图中画出梁的位移和惯性力，惯性力为三角形分布。

图2-12

图2-13

直接将质量取出作为隔离体并不方便。加上惯性力后，变成了一个形式上的静力学问题，可用结构力学位移法的基本体系建立平衡方程，其本质仍然是刚度法。为此在支座B处装上限制转动的附加约束。

首先锁住附加约束，画出结构在外荷载（包括惯性力）作用下的弯矩图MP，如图2-14（a）所示，并标出附加约束上的反力矩R1P。再画出节点B 上所受的力矩，如图2-14（b）所示。

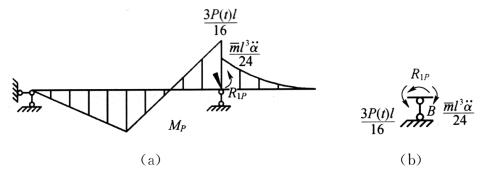
图2-14

由∑mB=0，得

则有

接着使附加约束沿α方向转动单位转角，并画出结构相应的弯矩图，如图2-15（a）所示。再画出节点B 上所受的力矩，如图2-15（b）所示。

图2-15

由∑mB=0，得

则

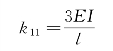
由结构力学位移法的基本方程k11α+R1P=0，得到此系统的振动微分方程为

还有一些振动系统，振动的恢复力（矩）为重力或其分力，或重力的矩，或介质对质量的压力、浮力等，如图2-16所示的单摆、光滑圆形滑道中做纯滚动的圆柱体、不完全浸没于液体中的物块的上下振动等。

图2-16

2.1.1.2 柔度法

与刚度法不同，柔度法不将质量取出作为隔离体，而是先勾画出结构的变形，考查质量所在处结构的变形；质量所在处结构的变形由外荷载和惯性力共同产生，写出变形方程，注意此时质量与结构间的作用力（恢复力）为内力，不应出现在变形方程中；用材料力学、结构力学的方法或已有结果求出变形方程中的柔度系数，代入变形方程并化简即得系统的运动微分方程。

由于用柔度系数描述外荷载、惯性力产生的位移，列变形方程，故名柔度法。

【例5】对例1中光滑水平面上的弹簧质量系统，用柔度法重新建立运动方程。

解：质量的运动、自由度和惯性力如图2-17所示。质量的位移可视为仅由惯性力产生，列出变形方程为

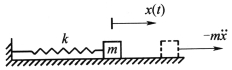
图2-17

式中，惯性力的柔度系数δ为单位力作用在质量上产生的位移，也就是单位力作用在弹簧上产生的变形量，而弹簧产生单位变形需要的力为k，因此

将柔度系数代入变形方程并化简，得

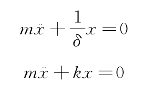
与例1用刚度法建立的运动方程最终是一致的。

注意：在同样的自由度坐标下，柔度法和刚度法得到的运动方程最终应相同。对单自由度系统，柔度系数和刚度系数互为倒数

一般对静定结构系统求柔度系数较方便，适合用柔度法。

下面讨论对外激励力不直接作用在质量上的静定结构系统，如何用柔度法建立运动方程？

【例6】如图2-18所示简支折杆的竖杆上端有一集中质量，水平杆中点受一简谐激励力作用。

图2-18

解：由于外激励力不直接作用在质量上，激励力和惯性力的柔度系数不同。结构的变形、质量的运动和自由度如图2-19所示，列出质量处变形方程，有

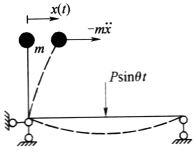
图2-19

画出两个单位力弯矩图2-20（a）、（b），由结构力学图乘法求得

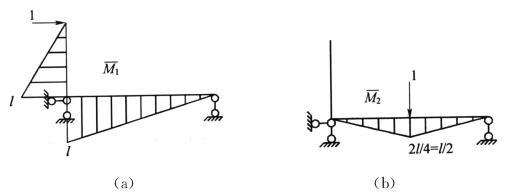
图2-20