振动系统模型的建立与分析

对结构进行振动分析，必须把所研究的对象以及外界对它的作用和影响简化为理想的力学模型。这个模型不但要简单，而且在动态特性方面应尽可能地与原系统等效。

任何结构之所以能产生振动，是因为它本身具有质量（Mass）和弹性（Spring）。从能量关系看，质量可以储存动能，弹性可以储存势能。当外界对系统做功时，系统质量吸收动能，因而就具有运动速度；而弹性元件储存变形能，因而就具有使质量恢复原来状态的能力。这样，能量不断地变换就导致系统质量的反复运动（振动）。然而，在没有外界干扰（激励）的情况下任何振动都会逐渐消失，也就是说，振动系统本身存在一种阻碍振动持续进行的阻力，这种阻力称为阻尼（Damping）。显然，如果没有外界源源不断地输入能量，由于阻尼的能量消耗，振动现象将逐渐停息。由此可见，质量、弹性元件和阻尼是振动系统力学模型的三个要素。下面对这三个要素的特性做出具体说明。

（1）质量。表示物体惯性的一种度量，即表示力与加速度的关系。在力学模型中一般将质量简化为刚体。

（2）弹性元件。表示力和位移的关系。通常被简化为无质量并具有线弹性的弹簧，即弹性力的大小与其两端点的相对位移成正比。若弹簧两端的相对位移用δ表示，则弹性力

其中，k 为弹簧刚度或弹簧常数，即使弹簧产生单位变形需要施加的力。

在许多实际问题中，经常遇到几个弹簧同时使用的情况，这时可以用作用在集中质量上的一个等效弹簧来代替。

设n 个弹簧的刚度系数分别为k1，k2，…，kn，等效弹簧的刚度系数用keq表示。图1-3分别是n 个弹簧并联、串联和与它们等效的单个弹簧系统。

n 个弹簧并联时，设每个弹簧的变形量为δ，则

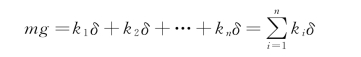
对图1-3（c）所示的等效弹簧有mg=keqδ，所以n 个弹簧并联时的等效弹簧刚度为

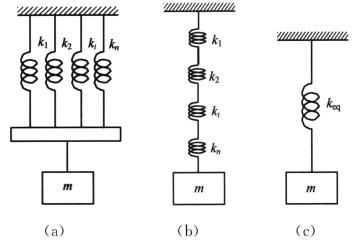
图1-3 弹簧的并联与串联

n 个弹簧串联时，各个弹簧受力相同，形变量为，总形变量

(www.xing528.com)

再利用如图1-3（c）所示的等效弹簧关系mg=keqδ，得到n 个弹簧串联时的等效弹簧刚度

（3）阻尼。是耗能元件，既不具有惯性，也不具有弹性，表示力与速度的关系。工程中不同结构的阻尼力与速度的关系是不一样的，阻尼力比弹簧力的分析要复杂得多。若阻尼力与速度的一次方成正比，则称此阻尼为黏性阻尼（Viscous Damping）或线性阻尼（Linear Damping）。若黏性阻尼器两端的相对速度用v 表示，则阻尼力

其中，c为黏性阻尼系数，使阻尼产生单位速度需要施加的力。

像弹性元件一样，在实际应用中，对于包含多个阻尼元件组成的振动系统，同样可以将这些阻尼用一个作用在集中质量上的等效阻尼来代替。黏性阻尼并、串联时的等效阻尼系数和弹簧并串联时的等效刚度系数类似，即将式（1-5）和式（1-6）中的k 换成c即可。

振动系统的模型可分为离散系统（Discrete System）与连续系统（Continuous System）。离散系统又称集中参数系统（Lumped Parameter System），由质量、弹簧和阻尼元件组成，因此，离散系统可简称为m-k-c系统。离散系统的运动在数学上用常微分方程表达，运算比较简单，因而在振动力学理论和实际工程中都得到广泛应用。连续系统由弹性体元件组成，典型的弹性体有杆、梁、轴、板、壳等。弹性体的惯性、弹性与阻尼是连续分布的，故又称为分布参数系统（Distributed Parameter System）。连续系统模型接近系统的原态，但相对离散系统模型一般要复杂得多，其运动在数学上表现为偏微分方程形式，运算分析比较困难，因此在必要的情况下才选用连续系统模型。

下面通过实例说明一个复杂振动系统的力学模型建立过程。

图1-4（a）是一个载人摩托车示意图，建立它在铅垂方向的振动模型。

模型1如图1-4（b）所示。等效刚度keq考虑了轮胎的刚度、支撑杆在竖直方向的刚度以及骑乘人员的刚度；等效阻尼ceq考虑了支撑杆在竖直方向的阻尼和骑乘人员的阻尼；等效质量meq考虑了轮胎、车身和骑乘人员的质量。

模型2～4如图1-4（c）～图1-4（e）所示。分别考虑车辆、车轮、轮胎、支撑杆和骑乘人员的质量、刚度和阻尼，将它们综合分析以后得到两自由度、三自由度和四自由度的振动模型。

由此可看出，同一个系统可以用多种力学模型来模拟，哪种模型最接近实际要进一步分析研究，这是解决工程振动问题的重要内容之一。

图1-4 载人摩托车的振动模型

下标说明：t：轮胎；w：车轮；s：支撑杆；v：车辆；r：骑乘人员；eq：等效