微观断口形貌特征：疲劳条纹间距的定量分析

疲劳条纹是微观断口形貌的主要特征，它与应力循环对应，其间距对应每一次应力循环的疲劳裂纹的扩展速率。Paris 在分析了大量疲劳裂纹扩展规律的基础上获得了如图3-22 所示曲线。

图3-22　疲劳裂纹扩展速率与应力强度因子关系曲线

图3-22 中直线段称为第二扩展阶段，可以推出式（3-3），称为Paris 公式：

式中，C、n 是与材料有关的常数，称为疲劳扩展材料常数，可由实验测定。在式（3-3）中，da/dN 的单位为mm/循环次数，ΔK 的单位为

实验结果表明，Paris 公式中的材料常数C、n 保持不变，材料微观组织、应力比、平均应力、载荷频率以及载荷波形等的影响都不明显。因此，使得Paris 公式可以应用于零部件疲劳断裂的定量分析。

1.Paris 公式定量估算疲劳扩展寿命[5－6]

由于一个疲劳条纹间距对应一次循环加载裂纹微观扩展速率，即条纹间距可粗略代表断口上该处的疲劳裂纹扩展速率，并大致认为与宏观疲劳扩展速率一致。通过扫描电镜等微观手段，由疲劳断口测出裂纹第二扩展阶段的疲劳条纹间距，利用从断口上测定的不同裂纹长度处的疲劳条纹间距值可定量分析疲劳扩展寿命。

若令每一载荷循环下的疲劳裂纹扩展量为μ，则

式中，a 为裂纹长度；N 为循环次数。

式中，a0 为裂纹开始扩展时的尺寸；ac 为发生瞬断时的裂纹尺寸，又称临界裂纹尺寸。

对于载荷谱加载，式（3-4）依然适用，只是此时N 为应力循环次数，da 为疲劳弧线间距。

代入式（3-3）中可用疲劳裂纹扩展速率反推疲劳扩展寿命的表达式：

式中，Y 为与裂纹有关的构件几何形状因子；Δσ 为最大应力σ max 和最小应力σ min 之差，a 为裂纹长度。

对给定构件及恒定交变载荷Δσ，则有

其中，A＝Y×（π）1/2×Δσ＝常数。

其中，C0＝C×An，则有

常数C0 和n 可由如下方法确定，即对式（3-5）取对数：

则lg（da/dN）与lga 为直线，截距为lgC0，斜率n/2。

在对裂纹长度a 和裂纹扩展速率da/dN 取对数并进行曲线拟合时，a 和da/dN 的量纲要统一。

对于不同裂纹长度ai 所对应的（da/dN）i 则可按式（3-7）进行拟合或分段拟合，求出C0 及n/2。随后可按式（3-6）求得N。举例说明如下：

【例3-14】　某大型构件发生疲劳断裂，通过对宏观断口与微观断口分析，求出式（3-5）中的C0 与n 值。

试验步骤：在扫描电镜下拍照不同裂纹长度a 处对应的疲劳条纹照片（照片见附录C），根据照片测定疲劳条纹的间距得到（da/dN）i 拍摄的照片并求出各自的对数值，测定结果见表3-1。

表3-1　测定裂纹长度与裂纹扩展速率

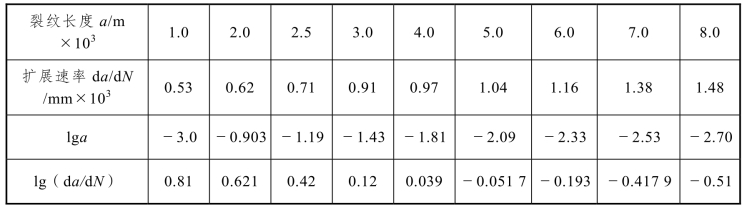
令lg（da/dN）＝Y，lg a＝X，lgC0＝b，（n/2）＝a，则式（3-7）可变成直线方程Y＝b＋aX。

利用高等数学知识最小二乘法公式求出a 与b 的值[5]。首先列表计算各自系数，再代入最小二乘法公式，求出各自系数，见表3-2。

表3-2　最小二乘法系数计算结果

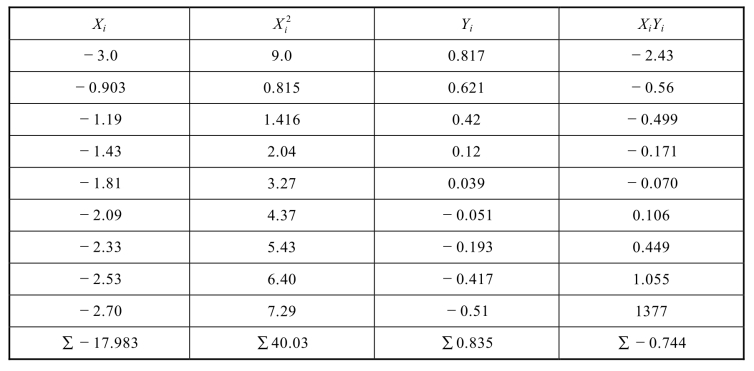
根据最小二乘法公式求出：a＝0.103，b＝0.27，根据式（3-7）求出式（3-6）中的n＝0.206，C0＝1.86。

需要注意的是：当采用不同的单位进行计算分析时，所得到的C0 与n 有很大差别。针对例3-10，对于裂纹长度a，采用μm 为单位，对于扩展速率da/dN，采用μm/循环次数为单位，读者可以自己再次进行计算。

求出n 与C0 后可以直接代入（3-6）中求出疲劳寿命值。式（3-6）中ac、a0 的确定：

（1）ac 是发生瞬时断裂时的裂纹尺寸，大致等于疲劳断口上疲劳源到瞬时断裂区域间的距离，可以从疲劳断口上测定。

（2）利用材料的抗拉强度按照下面方法计算[7]：

因为当净截面上σ＝σb 时零件破坏，随裂纹扩展零件的截面积减少应力值增加。当裂纹扩展达到ac 时，净截面上应力σ＝σb。但是在疲劳条件下，按照静载计算净截面应力σ 要乘一个动载荷系数（一般为1.15）作为外加应力修正值σ修正，当外加应力修正值σ修正＝σb 时，可以求出对应的截面积，从而求出ac。

（3）a0 是裂纹开始扩展尺寸，如何确定目前无统一标准。美国空军制定为 1/32 英寸（0.794 mm）对应a0。美国惠普公司规定a0＝0.38 mm，英国罗罗公司规定a0＝0.15 mm[3]。从宏观断口上分析a0 对应的值应该是从疲劳源到最早出现疲劳条纹间的距离。因此可以根据具体情况进行确定a0。

根据断口疲劳条纹测定结果，取对数之后的数值点有规律地分布在拟合曲线（直线）的两侧，说明裂纹长度和疲劳条纹间距值分别取对数之后有较好的线性相关性。如果取对数之后的数据拟合得到的是折线，见图3-23，则可以采用分段利用Paris 公式进行计算的方法[5]。通过对数据拟合的直线获得两个常数，代入相应的公式求疲劳裂纹的扩展寿命。

图3-23　取对数的数据得到的是折线

2.Paris 公式定量估算疲劳应力

在工程应用中，有多零部件承受恒应力幅或近似恒应力幅的载荷。因此可以根据断口测定数据，利用Paris 公式估算疲劳应力。即使零部件承受的并非恒应力负值，即使是复杂载荷作用，利用Paris 公式进行断口估算出当量恒应力幅应力也是很有参考价值的。

将Paris 公式展开：

式中，Y 是与裂纹有关的形状因子，对于标准试样和一些简单的裂纹形状，已有准确的形状因子表达式[6]，Y 也可用解析式计算求得或由实验测得。式中c 和n 可由实验测定。在c、n和Y 已知的条件下，再由疲劳断口的疲劳条纹宽度S 测得裂纹扩展速率da/dN，就可以根据Paris 公式反推出疲劳应力变幅Δσ：

对式（3-9）的说明如下：

（1）随着裂纹的扩展，疲劳应力是不断变化的。式（3-9）表明的是：不同裂纹长度位置对应的疲劳应力变幅的值。(www.xing528.com)

（2）S 为疲劳条纹间距。式中的S 是距离裂纹源某一位置的疲劳条纹间距值。在此位置处也对应一定的裂纹长度a，是通过测量此处的疲劳条纹间距得到的。

（3）Y 为裂纹形状因子。在确定Y 的过程中，一般需要结合构件及其细节的形状，构件的受载情况由裂纹尖端的应力强度因子模型来确定，大多数情况下Y 通过《应力强度因子手册》确定，在《应力强度因子手册》[6]中给出Y 的形式有图和表，也有公式。由于裂纹在扩展过程中长度不断变化，所以Y 值也随裂纹长度变化而变化。

（4）C、n 料参数。C 对应着国际单位制（da/dN 的单位为 mm/循环次数，K 的单位为）。使用相关手册查找C、n 值时需要注意采用的单位。当在不同的da/dN 与ΔK 单位制中转换时，n 值保持不变，但材料常数C 应视为有量纲的量，它的量纲是（应力强度因子）－n×长度单位。C 的单位与参与拟合的da/dN 数据及ΔK 的单位密切相关。

（5）利用疲劳条纹间距反推疲劳应力的关键在于确定上述参数值。在估算疲劳应力时，疲劳条纹间距S 的单位为mm，裂纹长度a 的单位为m，得出的应力单位为MPa。

（6）在具体应用中，由于不同的裂纹形状，具有不同的强度因子，所以应用式（3-9）会有一定的修正。

求出疲劳应力变幅Δσ 后，可求出最大应力 σmax=Δσ/（1 - R），式中R＝σmin/σmax，循环特征参数几种可供参考的确定R 值的情况如下[5]：

（1）对于脉动循环（实例：齿轮或轴服役条件下的单向弯曲），R＝0，σmax＝Δσ；

（2）对称循环（实例：车轴、曲轴服役条件下弯曲载荷），R＝－1，σmax＝－σmin；

（3）不对称循环（实例：有预紧力的螺栓），1＞R＞－1，σmax＝σm＋σa，σmin＝σm－σa，σm 为平均应力，σa 为应力幅值；

（4）静载荷，R＝1，σmax＝σmin＝σm；

（5）叶片离心应力的计算，由于叶片的疲劳扩展属于发动机起动次数为循环的低周疲劳，即R＝0，σmax＝Δσ；

（6）叶片的振动应力分析，振动破坏为对称循环，R＝－1，σmax＝Δσ/2；

（7）旋转弯曲疲劳的情况：R＝－1，σmax＝Δσ/2。

利用式（3-9）估算疲劳应力时，关键要知道Y、C、n 的值。前面已经论述，很多情况下Y 可以查出，通过测定不同裂纹长度处的疲劳条纹间距，可以求出C0 与n 值，并有以下公式：

但果，如果不知道材料的C 值，就难以通过式（3-9）求出疲劳应力。材料常数C、n 值一般是通过试验获得的，根据Paris 公式：

可知lg（da/dN）与lg（ΔK）存在直线关系，通过测定裂纹扩展速率试验的方法，得到ΔK 和da/dN，拟合指定数据段中的lg（da/dN）－lg（ΔK）数据，根据其斜率与截距获得C、n 值。C、n 值与材料状态、厚度及使用条件相关，在选用C、n 值要注意故障件的各条件状态与C、n值的试验条件之间是否一致。

在难以进行上述试验条件下，可考虑采用利用材料断裂韧性估算材料的C 值。

根据疲劳断裂过程可知，随裂纹的不断扩展，裂纹处的应力是逐渐增大的。前面论述ac对应临界裂纹长度，疲劳裂纹的尺寸扩展到ac 就要发生瞬时断裂，所以ac 代表疲劳扩展区域的大小，这是一个可以测量的值。裂纹达到ac 时，裂纹扩展的应力达到最大值σmax，可以推导出ac 与σmax 间的关系。

根据断裂力学理论有以下公式：

式中，Y 为裂纹形状因子；a 为裂纹长度；σ 为构件承受的应力；KⅠ为应力强度因子。

当a＝ac 时裂纹快速扩展，KⅠ达到临界值KⅠc，称为材料的断裂韧性。这时应力达到最大值σmax，所以有公式：

如果已经知道材料的断裂韧性KⅠc，从断口上可以测定出ac 值，在已知Y 的情况下就可以求出σmax。此处的σmax 是裂纹扩展距离达到ac 时对应的应力值。KⅠc有标准的试验方法可以进行测定，目前对于许多材料KⅠc是可查到的。同时KⅠc与材料的冲击韧性也存在一定关系，例如[8]：

CVN 是材料V 形缺口冲击韧性值，式（3-13）适用于屈服强度在780～1 730 MPa，冲击韧性CVN 在22～120 N·m 的钢。因此可以根据测定的强度与冲击韧性值估算出KⅠc，再根据式（3-12）可以估算出σmax 值。近似认为σmax 是式（3-9）Δσ 中的最大应力值，在已知载荷类型条件下可以知道最小应力值，因此可利用式（3-10）估算出材料的C 值。

在3.2.1 节中论述，可以从宏观断口利用材料的抗拉强度估算出疲劳应力，该应力可近似作为平均应力值。利用KⅠc估算出最大应力值，从而估算出R 值。

【例3-15】　用于飞机发动机中由钛合金材料制备的叶片在使用过程中发生断裂。断口的宏观形貌见图3-24，从图3-24 中可见，它属于疲劳断裂且裂纹形貌属于半椭圆裂纹。已知服役过程中既有离心力又有弯曲振动应力。采用纯弯曲应力作用下模型估算不同长度处应力强度因子范围。应力比R＝－1。

根据断口分析，测定出某一位置处断口形貌数据：

椭圆裂纹半短轴a＝0.28 mm（沿裂纹扩展方向的裂纹长度）；

椭圆裂纹半长轴b＝0.79 mm；

裂纹扩展速率S＝0.15 μm，形状因子Y＝1.1；

材料常数测定结果（裂纹长度，m；扩展速率，mm）：C＝4.66×10－12，n＝4.66。

估算服役条件下该位置处的应力值（注：此例选用文献[5]中案例）。

图3-24　宏观断口及微观断口照片[5]

分析：对于半椭圆表面裂纹，结合应力强度因子与Paris 公式，式（3-9）修正为

式中，E（k）为第二类完全椭圆积分E（k）＝[1＋1.464（a/b）1.65]1/2。

将测定的试验数据代入式（3-14），代入时注意裂纹长度a，单位用m，裂纹扩展速率S的单位用mm，求出Δσ 约为1 400 MPa。

因为R＝－1，σmax＝Δσ/2，求出σmax 约为700 MPa。

【例3-16】　用于大型装备中的螺栓发生断裂，螺栓材料为350CrMo，宏观与微观断口的宏观形貌见图3-25，从图3-25 中可见属于疲劳断裂，认为裂纹源处裂纹形貌属于圆片状裂纹。已知服役前螺栓施加一个预紧力约400 MPa，估算工作时最大应力。

图3-25　断裂螺栓裂纹源处断口形貌

分析：

（1）根据图3-25 可以测定出S＝25 μm＝25×10－3 mm；a＝0.75 mm。

（2）认为螺栓服役条件下受到拉-拉载荷，最小载荷就是预紧力400 MPa。

（3）根据原型表面裂纹特点采用式（3-15）估算最大应力。应力强度因子将式（3-9）修正为

根据圆形表面裂纹特征，确定Y＝1.1，Q＝1.55。

（4）材料参数C 与n 无法从实验获得，按照一般低合金钢选取数据[6]：

读者可以自己将数据代入式（3-15）中，求出最大工作应力。