材料模型和本构关系的附录C优化

C.1 概述

SOLIDWORKS Simulation集成了几个数学材料模型来模拟复杂的工程材料。用户可以根据企业的现实意义和可用的实验数据来选择材料模型。可以集成到SOLIDWORKS Simulation非线性模块中的材料模型被广泛定义为：

● 弹性模型。

● 弹塑性模型。

● 镍钛合金模型。

● 线性粘弹模型。

● 蠕变模型。

C.2 弹性模型

弹性材料模型的特点是载荷的加载、卸载、重新加载都会沿着同一应力路径进行。SOLIDWORKS Simulation包含下列弹性模型：

1）线性弹性模型。

2）非线性弹性模型。

3）超弹性模型。

①Mooney-Rivlin模型。

②Ogden模型。

③Blatz-Ko模型。

C.2.1 线性弹性模型

这类材料都遵循胡克定律，当增加或减少载荷时，应力和应变成比例变化，如图C-1所示。

这类材料模型的一些特征如下：

1）材料特性可以是各向同性的，也可以是正交各向异性的。各向同性的材料在各个方向拥有类似的特性，并通过弹性模量E和泊松比ν定义。

2）正交各向异性材料在不同方向展示不同的特性，并提供三个互相垂直的弹性对称基准面（三个主要的材料方向）。这类材料更为复杂，它由9个独立的材料常量来说明。

3）如果包含热力载荷，则必须提供材料常量，如热导率K、热膨胀系数α以及比热C。

4）温度相关性也可以和所有力学属性相关联，例如弹性模量通过熟知的交叉性相关系数来建立关联。

C.2.2 非线性弹性模型

和线弹性模型不一样，这个模型的应力-应变关系被认为是非线性的，如图C-2所示。

图C-1 线性模型（沿同一路径加载和卸载）

图C-2 非线性模型

该材料模型的一些特征如下：

1）只适用于各向同性材料。

2）必须给程序提供连续的应力-应变曲线。

3）应力-应变曲线在拉伸和压缩阶段可以不同，这样可以表现在拉伸和压缩加载过程中不同的材料响应。如果不指定压缩部分的曲线，SOLIDWORKSSimulation则会假定拉伸和压缩的行为类似。数据点必须按照应变增加的方向输入（从ε₁～ε_n）。

4）热膨胀系数、泊松比、密度也可以是与温度相关的量。

C.2.3 超弹性模型

超弹性材料的特点是它能在相对小的应力作用下产生大的应变（例如橡胶）。超弹性的名称来自在小载荷下发生大变形的能力。

尽管将材料视为弹性的，但它们的表现极为复杂，而且取决于加载模式。图C-3所示为一个典型的超弹性材料“应力-拉伸比”图表的加载分支。

图C-3 超弹性模型

提示

对超弹性材料，通常输入应力-拉伸比图表，而不使用应力-应变图表。下面给出了拉伸比λ与应变ε的关系

λ=1+ε

式中，ε为工程应变。

由于超弹性材料表现的复杂特性，它们的弹性常量源自弹性应变能密度函数（通常以W表示）。基于这个特定的模型，必须给SOLIDWORKSSimulation提供确定的材料常量。

SOLIDWORKSSimulation中的超弹性模型有以下三种：

● Mooney-Rivlin模型（M-R）。

● Ogden模型（OHE）。

● Blatz-Ko模型。

1.Mooney-Rivlin模型（M-R） 这是最常用的超弹性模型，因为很容易从材料制造商获得材料常量。下面列出了这个模型的一些材料特性：

1）Mooney-Rivlin材料模型可以使用2个、5个或6个常量来定义（2—常量M-R模型，5—常量M-R模型等），可以直接从SOLIDWORKS Simulation的【材料】对话框中输入，如图C-4所示。请注意，在【属性】选项卡中，【模型类型】必须选择【超弹性-MooneyRivlin】。

2）前两个Mooney-Rivlin常量的和必须一直大于零，即A+B>0。

3）如果可以提供简单张力、平面张力、双轴性张力的“应力-拉伸比”曲线，SOLIDWORKS Simu-lation便能够推导出Mooney-Rivlin常量。尽量只需要三条曲线中的一条即可得出，但还是强烈建议提供所有三条曲线，以确保结果更可靠。用户可以在【材料】对话框的【表格和曲线】选项卡中输入曲线，如图C-5所示。

4）2—常量M-R模型适合应变达150%的实验数据。实验情形包含简单张力、纯剪切和等轴拉伸。

5）在缺乏实验数据的情况下，如果给定弹性模量E，则可以近似假设A和B系数为

A=0.8E

B=0.2E

6）使用常量C～F，可以扩展模型应变的有效性高达600%。为了保证不可压缩性（橡胶为近乎不可压缩材料），泊松比必须在0.48～0.5，推荐数值为0.499～0.4999。

图C-4 模型特征

图C-5 输入曲线

2.Ogden模型（OHE） 对于橡胶这样的不可压缩材料，选择Ogden的超弹性模型是另外一种常用办法。它的弹性应变能密度函数在描述橡胶类材料的大变形时被认为是最成功的。下面列出了这种模型的特性，如图C-6所示。

1）修正的3-常量Ogden模型被广泛应用，它能描述橡胶材料的变形，应变高达600%。

2）SOLIDWORKS Simulation可以指定多达4个常量（一对常量α_{1，2，3，4}和μ_{1，2，3，4}）。

3）2—常量M-R模型（常量A和B）是2—常量Ogden模型（常量α₁，α₂，μ₁和μ₂）的一种特殊形式。在这种特殊形式下，两个模型常量之间的关系为

α₁=2

α₂=-2

μ₁=2A

μ₂=-2A

4）Ogden模型的计算效率可能比Mooney-Rivlin模型要低。

5）如果不知道这些常量的大小，用户可以输入材料曲线（和Mooney-Rivlin模型中的情况一样）。为了保证不可压缩性，推荐泊松比数值为0.499～0.4999。

图C-6 模型特征

3.Blatz-Ko模型 对于像泡沫类的可压缩超弹性材料而言，Blatz-Ko模型比Mooney-Rivlin模型和Ogden模型更加合适。该模型只需要弹性模量E这一个材料常量。假定泊松比ν=0.25。

超弹性模型的一般注意事项

● 推荐使用NR（牛顿拉夫森）迭代法。

● 如果结构受到压力载荷，请使用位移相关的加载选项。

● 0.48≤ν<0.5是可以接受的。

● 当处理橡胶类材料时，由于问题的高度非线性，快速增加的载荷经常导致数值不稳定（刚度产生负的对角线项）和平衡迭代时发散。在这种情况下，自动步进算法可以起到帮助作用。

● 在各种加载速率下，如果经常发生负的对角线项（数值不稳定），采用位移或弧长控制方法可能比力控制方法更加有效。

● 对壳单元而言，分析更为简单，因为公式可以通过假定完美的不可压缩性（ν=0.5）而推导得出，因此可以忽略NUXY。

C.3 弹塑性模型

当质点应力超出屈服点时，弹性材料模型不再有效。在这种情况下，必须使用弹塑性模型的能力来描述后屈服问题。

C.3.1 弹塑性模型的基本特征

弹塑性模型区别于弹性模型的基本特征有：

● 沿不同曲线加载和卸载载荷。

● 路径相关。

● 交变加载的表现。

1.沿不同曲线加载和卸载载荷 如果材料加载了超过屈服强度的载荷，当完全移除载荷后，材料将会产生永久变形ε_永久。如果材料重新加载载荷，则会沿着之前卸载的路径加载。产生的结果是，屈服点发生移位，材料变硬（应变硬化），如图C-7所示。

2.路径相关 如果最终应力相同，但加载历史不同，则会产生不一样的应变，如图C-8所示。

3.交变加载的表现 如果金属受到周期性的拉伸和压缩，每次改变加载模式（拉伸/压缩）后的屈服点都会不同，这种现象称为包辛格效应，如图C-9所示。

图C-7 应变硬化

图C-8 加载路径

图C-9 包辛格效应

提示

每完成一次加载周期，包辛格效应的影响就会减弱。在足够数量周期后（>1000），材料将趋于稳定，包辛格效应也会消失。对这样达到稳定的材料所对应的应力-应变曲线，我们称之为交变的应力-应变曲线，这和“全新的”材料样本所产生的传统的单向曲线有非常大的区别。因此，如果产品加载这类载荷，也应该使用稳定的交变材料曲线来进行应力分析。

C.3.2 弹塑性的三要素(www.xing528.com)

为了理解材料屈服后的行为，必须掌握下面三个要素：

● 屈服准则。

● 硬化规律。

● 流动法则。

1.屈服准则 屈服准则是指定多向应力相对于塑性流动开始的状态。用户有多种准则可选，而每

种适用于不同类型的材料。例如，Tresca屈服准则假定屈服发生在最大剪切应力（质点低于一般的应力

状态）达到单向拉伸试验时屈服发生时的最大剪切应力。Von Mises准则假定屈服发生在变形能（质点低于一般的应力状态）等于单向拉伸试验中开始屈服时的变形能。

2.硬化规律 硬化规律定义了在塑性流动过程中，加载和卸载对材料的屈服强度的影响，如图C-10所示。

如果加载模式发生更改（拉伸或压缩），则必须考虑包辛格效应。SOLIDWORKS Simulation集成了下面三种硬化规律：

（1）各向同性硬化 该规律忽略包辛格效应并假定在交变加载时，当前屈服点的数值并不会随着加载模式的变化（拉伸/压缩）而发生改变。材料的应变硬化是各向同性的，也就是说，材料的硬化体现了各向同性的特性，如图C-11所示。

在SOLIDWORKS Simulation中，用户可以通过指定硬化因子RK为0来表示各向同性硬化。

（2）运动硬化 该规律通常高估了包辛格效应，材料的应变硬化呈现非各向同性，也就是说，材料硬化体现了非各向同性的特性，如图C-12所示。

图C-10 硬化规律

图C-11 各向同性硬化

图C-12 运动硬化

在SOLIDWORKS Simulation中，用户可以通过指定硬化因子RK为1来表示运动硬化。

（3）混合硬化 现实世界中，大多数金属都可以通过组合各向同性硬化和运动硬化规律来描述其特性。部件之间总体塑性应变的关系可以表现这种组合

dε^p=dε^p_isotropic+dε^p_kinematic （C-1）

式中，dε^p_isotropic=（1-RK）×dε^p，dε^p_kinematic=RK×dε^p。

在式（A-1）中，dε^p是总体塑性应变增量，它可以分为各向同性（dε^p_isotropic）部分和运动（dε^p_kinematic）部分。

3.流动法则 流动法则定义了塑性应变增量、当前应力、屈服后应力增量之间的关系。所有SOLIDWORKSSimulation模型都使用一个关联流动法则，其中塑性应变增量都朝着垂直于当前屈服表面的方向。非关联流动作为一个替补法则，也与之并存，而且是很多学者的研究课题。

C.3.3 弹塑性模型的类型

SOLIDWORKS Simulation包含下列弹塑性模型：

● vonMises。

● Tresca。

● Drucker-Prager。

1.vonMises vonMises塑性模型基于下列等效假设：一个质点受到一般应力，当该质点累积的变形能和一个质点在单向拉伸开始屈服时累积的变形能相等时，屈服就会发生。在各向同性材料里，该假设用数学表达式可以表示为

式中，σ_y是单向应力-应变曲线对应的当前屈服应力；G是剪切模量；S_ij是偏应力分量。

其中，表达式的左右两侧分别代表质点在单向开始发生屈服时的偏能量，以及一般应力状态的情况。

提示

一般应力状态可以通过第二级应力张量σ_ij表达，它可以分为两个部分

式中，σ^H_ij是静水应力张量分量（各个方向应力相等，与物体浸入水中的感觉一样）；S_ij是偏应力张量分量。

按照vonMises的假设，可以得出结论：只有S_ij的分量与材料的屈服有关，也就是说，无论有多大的压力，受到静水压力的物体都不会发生屈服！

将之前偏能量的方程式孤立出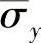，得到

式中，σ_VM是von Mises应力，表示刚发生屈服时一般应力状态应力分量的组合。请注意，σ_VM和从单向拉伸试验中得到的进行对比，而且σ_VM通常为正值。

SOLIDWORKS Simulation中von Mises模型的一些基本特征如下：

（1）双线性应力-应变曲线 在很多例子中，复杂的应力-应变曲线可以很方便地通过两个线性函数逼近，如图C-13所示。

图C-13 逼近函数

在【材料】对话框中，可以输入E、ν、E_t和σ_y的数值，如图C-14所示。

图C-14 材料参数

（2）多线段应力-应变曲线 完全拉伸的应力-应变曲线也可以输入到表格中，如图C-15所示。请注意，表格中第一个点必须是初始屈服点，曲线必须是单调的，而且假定压缩时也是类似的特性。在【属性】选项卡中，直接输入的任何弹性模量和屈服强度都将被忽略。

图C-15 曲线数据

提示

SOLIDWORKS同时提供大应变小应变两种应变塑性公式。对大应变塑性问题，必须给定真实应力与真实（对数的）应变之间的单向应力-应变曲线。

2.Tresca Tresca屈服准则假定，在一个简单拉伸试验中和一般应力状态下，当质点的最大剪切应力值达到屈服开始发生时的最大剪切应力时，屈服就会发生。该准则通过数学语言可以表达如下

㊀ P₁为σ₁，P₃为σ₃，σ_y为σ_s。为与软件保持一致，此处未做改动，请读者注意。——编者注

式中，P₁和P₃分别代表最大主应力和最小主应力的值；τ_max是一般应力状态下的最大剪切应力；σ_y是在单向拉伸试验中材料当前的屈服强度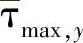；发生屈服时的最大剪切应力。

P₁-P₃的数值一般被作为应力强度，而且可以在SOLIDWORKS Simulation中绘制图表。

在现实世界中，大多数金属的屈服强度都可以通过vonMises和Tresca准则进行预测，Tresca准则显得更为保守。Tresca模型的基本特征和von Mises模型大部分相同，只是Tresca模型不支持大应变塑性公式。

3.Drucker-Prager Drucker-Prager模型可以用于模拟颗粒土壤材料的特性，例如砂砾石。该模型只需要两个材料参数进行定义：内摩擦角ϕ（0°≤ϕ≤90°）以及材料的粘合强度c（c≥0）。该模型不支持大应变塑性公式，推荐采用牛顿-拉夫森迭代技术。

C.4 镍钛合金模型

镍钛合金是一类独特的材料，也就是我们熟知的记忆金属，该材料的热-弹性马氏体相变是该独特性能的主因。这些属性包含记忆效果、超弹性和高衰减能力。镍钛合金可以经受20%的大应变，而在卸载后不会表现出任何永久变形。

如图C-16所示，材料最初表现为弹性，直到应力水平达到加载过程中的初始屈服应力σ^t_s1。如果继续加载，材料变软并表现出弹塑性，直到达到加载过程中的最终屈服应力σ^t_f1。如果加载超过σ^t_f1的载荷，则材料会加速硬化。

当载荷卸载时，材料表现为弹性，直到应力水平达到卸载过程中的初始屈服应力σ^t_s2。如果继续卸载，材料表现出弹塑性，直到应力水平达到卸载过程中的最终屈服应力σ^t_f2，而且累积的塑性应变（从加载阶段开始）也消失了。从这一点开始，材料会按弹性模式卸载，直至回到最初的形状，而没有任何永久变形。

类似的现象在压缩部分也可以观察到。

镍钛诺应力-应变图表的数据点是在【材料】对话框的【属性】选项卡中以表格的形式输入的，如图C-17所示。

图C-16 镍钛合金模型的单轴性应力-应变关系

图C-17 输入材料参数

流动规则 和弹塑性材料的情况一样，当发生软化时，必须介绍屈服准则和主导该现象的流动规则。应力-应变曲线上，我们把加载过程中初始屈服应力和最终屈服应力点之间的区域称为上峰。对应卸载过程中的区域称为下峰。这些峰的形状由流动规则来决定。流动规则的参数β^t1、β^t2、β^c1、β^c2可以在【属性】选项卡中指定，它们分别控制加载和卸载过程中拉伸和压缩的速度和变形形状，如图C-18所示。如果不指定流动规则参数，两个峰都将是线性的。

图C-18 应力-应变曲线

C.5 线性粘弹性模型

目前，讨论的所有弹性模型的一个共同特点是它们的速率具有独立性，也就是说，当移除载荷时，无论加载的速率如何，它们都将沿着在应力-应变曲线上相同的加载路径。

粘弹性材料是不同的，它们的特性取决于加载载荷的速率，使得它们的特性和应变率有关。因此，不同的加载（卸载）速率对应不同的加载（卸载）路径，而最终载荷大小可能是相等的，如图C-19所示。这些材料由于具有粘性效应，因此可以消耗机械能。

图C-19 线性粘弹性模型

对多轴应力状态，SOLIDWORKS Simulation使用下面的本构关系

式中，和分别是偏应变和体积应变；G（t-τ）和K（t-τ）分别是剪切松弛函数和整体松弛函数。

定义材料常量如何随时间变化的松弛函数，可以通过GeneralizedMaxwell模型（广义麦克斯韦模型）表现出来：

用数学表示为

式中，G₀和K₀分别是瞬时剪切模量和瞬时体积模量；g_i和k_i分别是对应时间τ_i^G和τ^K_i的剪切模量和体积模量。

两个松弛函数都可以直接通过相应的时间曲线输入，用户可以在【材料】对话框中的【表格和曲线】选项卡中输入，如图C-20所示。

当然，用户也可以在【材料】对话框中的【属性】选项卡中输入一组离散的点（最多8个），如图C-21所示。

粘弹性的特性与温度具有很大关系，说明温度效应的一种方法是使用移位函数。在时间τ处的松弛函数移位到时间γτ，其中γ为移位函数）。在SOLIDWORKS Simulation中，WLF（Wiliams-Landel-Ferry）方程可以作为γ的近似函数使用

式中，T₀是参考温度（通常为玻璃化转变温度）；C₁和C₂分别是与材料相关的常量。

图C-20 【表格和曲线】选项卡

图C-21 从【属性】选项卡中输入

如果在分析中考虑温度效应，必须在【材料】对话框的【属性】选项卡中指定T₀、C₁和C₂的值，如图C-22所示。

图C-22 输入参数值

C.6 蠕变模型

蠕变是一种与时间相关的应变，它在一个恒定的应力状态下产生，而且在工程材料中可以观察得到，例如高温下的金属、高分子聚合物以及混凝土。图C-23所示为蠕变曲线，显示了应变和时间之间的关系。

总体而言，蠕变可以分为三个阶段。第一阶段（减速蠕变）开始的速率很快，然后随时间逐渐慢下来。第二阶段（恒速蠕变）具有相对恒定的速率，而第三阶段（加速蠕变）的速率又重新增大，并结束在材料断裂时刻t_R。

蠕变和应力水平、时间和温度的关系密切。幂定律（Bailey-Norton定律）集成在SOLIDWORKS Simulation中，它表达了单向蠕变应变和单向应力σ、时间t和温度T之间的关系

式中，C₀、C₁（C₁>1）和C₂（0≤C₂≤1）是与材料相关的蠕变常量；T是绝对温度（K）；C_T是定义蠕变温度相关性的材料常量。

图C-23 蠕变曲线

请注意，在SOLIDWORKS Simulation中使用的蠕变经典幂定律只代表第一和第二蠕变阶段。

为了扩展单向蠕变定律到多向蠕变特性，需作出下列假设：

● 如果单向蠕变应变和应力被等效应变和应力所替代，单向蠕变定律仍然有效。

● 蠕变应变是不可压缩的。

● 材料是各向同性的。