本节将通过超弹性-Mooney Rivlin模型,使用单向拉伸实验数据来计算材料参数。操作步骤
步骤1 打开零件
打开Lesson13\Case Study文件夹下的文件Pipe。
步骤2 新建算例
在第一个算例中,将使用单轴实验数据来确定橡胶的材料属性。新建一个【非线性】算例并命名为Uniaxial Test Data。
步骤3 定义壳体
右键单击Pipe实体并选择【按所选面定义壳体】来定义壳体,选择pipe的外表面,设置【抽壳厚度】为0.75mm,指定为【细】壳体类型,如图13-2所示。
步骤4 应用材料
右键单击Pipe文件夹,选择【应用/编辑材料】。定义一个名为U-niaxial的自定义材料,【模型类型】选为【超弹性-Mooney Rivlin】材料。确认【常量数】设定为2,设置【泊松比】为0.49,【质量密度】为1020kg/m^3,如图13-3所示。
勾选【使用曲线数据来计算材料常量】复选框,弹出【表格和曲线】选项卡,如图13-4所示。
步骤5 输入实验数据
在【类型】选项组中,选择【简单张力】。确认【单位】设定为【牛顿/m^2】。从名为uniaxial.xls的电子表格中复制并粘贴数据,如图13-4所示。

图13-2 定义壳体

图13-3 编辑材料
单击【保存】、【应用】、【关闭】,保存材料属性。
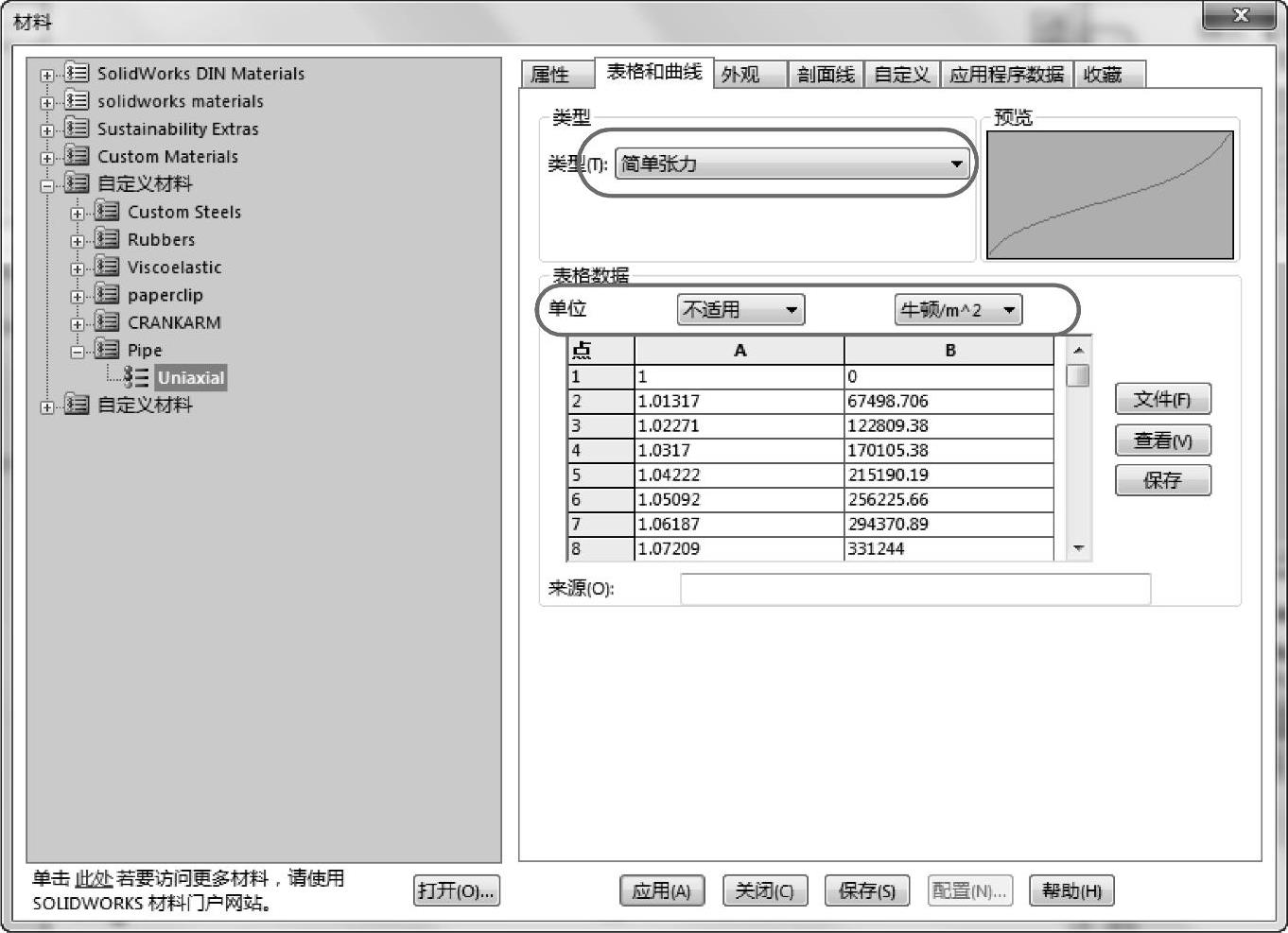
图13-4 输入实验数据
步骤6 添加夹具
右键单击【夹具】,选择【固定几何体】。
选择管子的两个端面(图13-5),然后设置约束【标准】为【固定几何体】。确认选择的是外表面,因为这是定义壳体的位置。

图13-5 添加夹具
步骤7 添加压力
右键单击【外部载荷】,选择【压力】。除了端面以外,选择模型的所有外表面。输入1.5e5N/m^2的压强值并单击【反向】(压力的方向朝外)。确认【随时间变化】选为【线性】,如图13-6所示。
 (https://www.xing528.com)
(https://www.xing528.com)
图13-6 添加压力
步骤8 生成网格
使用默认网格大小生成【草稿品质网格】,使用【标准网格】。
步骤9 设置非线性算例属性
设置【开始时间】为0,【结束时间】为1,【时间增量】选择【自动】。设置【初始时间增量】为0.01,【最小】为1e-8,【最大】为0.2,【调整数】为5。单击【高级选项】,确认【控制】方法设定为【力】,【迭代方法】为【NR(牛顿拉夫森)】。
步骤10 运行算例
分析一般不会超过1min完成计算。
步骤11 查看结果
对最后一个时间步长图解显示位移量并留意最大位移(2.274mm),如图13-7所示。
步骤12 检查材料模型
在Windows资源管理器中,根据保存结果路径找到文件Pipe-Uniaxial TestData.LAG和Pipe-Uniaxial Test Data.PLT。两个文件都是ASCII文本文件,包含了所有需要的材料模型数据。在记事本或写字板中打开这两个文件并查看它们的内容。∗.LAG文件中包含计算的Mooney-Rivlin常数,如图13-8所示。
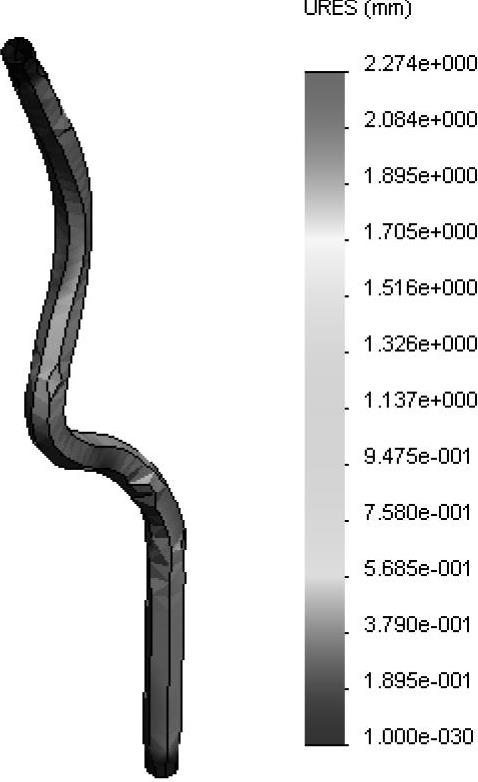
图13-7 位移结果
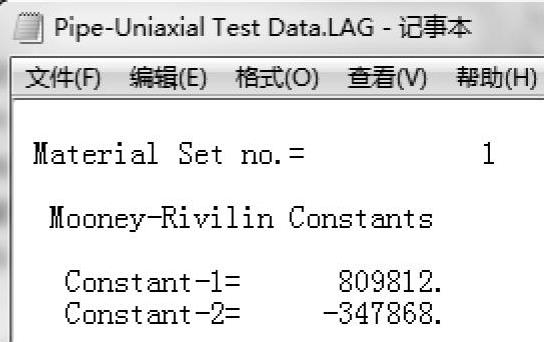
图13-8 ∗.LAG文件内容
提示
材料的常数也显示在解算器信息中,右键单击【结果】文件夹并选择【解算器信息】。
∗.PLT文件包含一个表格,对比了使用这个材料模型计算得到的应力值,和在不同拉伸比下实验数据输入到SOLIDWORKS Simulation的应力值,如图13-9所示。
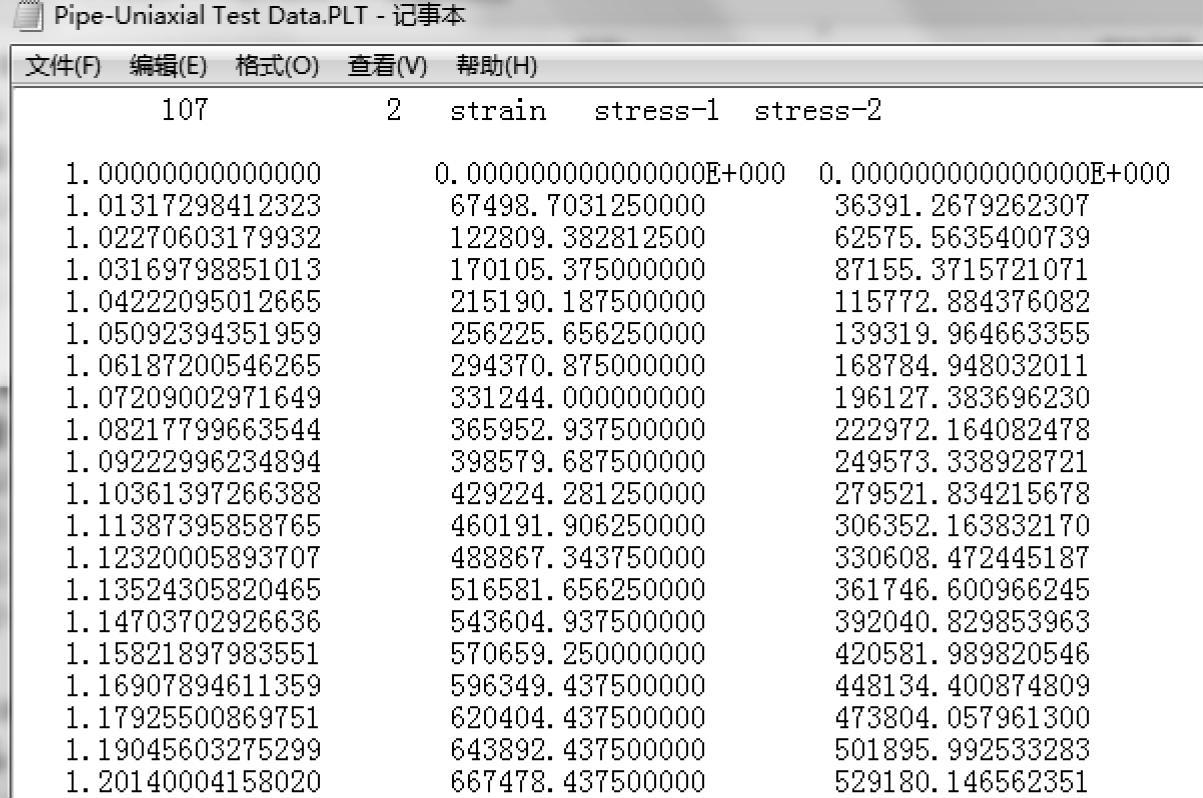
图13-9 ∗.PLT文件内容
表格的第一列给出了输入到程序中的拉伸比。第二列给出了对应的应力值(单位为N/m2),表头为Theory的第三列,列出了使用Mooney-Rivlin材料常数计算得到的应力值。提示
第一列的表头表示为strain,然而这实际上是拉伸比。∗.PLT文件中的应力值以SI单位(N/m2)表示,如图13-10所示。
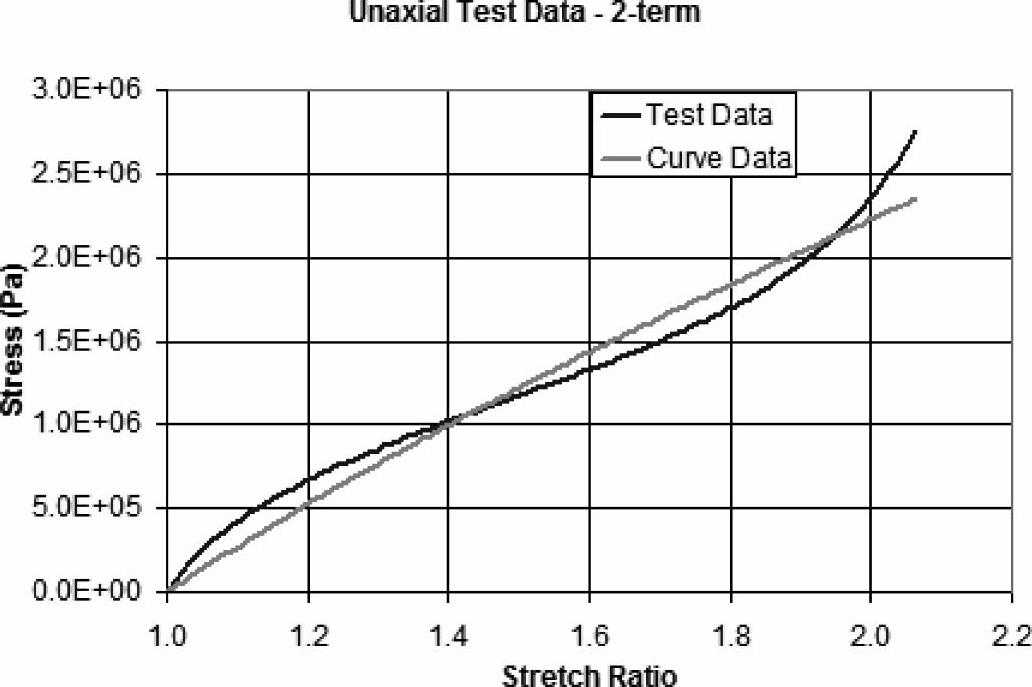
图13-10 数据对比图
在上面的步骤中,我们只用了单轴实验数据和Mooney-Rivlin材料模型的两个常数。查看∗.PLT文件后可以很清楚地看到实验数据和理论应力值之间的差别还是很大的。因此,有必要使用更多的实验数据和更精细的材料模型来运行这些计算。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




