如何进行各向同性硬化？

图12-1 曲柄模型

我们要研究的第一种硬化规律是各向同性硬化，在各向同性硬化过程中忽略包辛格效应，加载发生改变时屈服点是不变的。操作步骤

步骤1 打开零件

打开Lesson12\CaseStudy文件夹下的文件CRANKARM。

步骤2 生成算例

新建一个【非线性】算例并命名为Isotropic。

步骤3 添加约束

对模型基体部分的内侧圆柱面添加【固定几何体】夹具，如图12-2所示。

步骤4 应用材料

使用双线性应力-应变曲线的von Mises弹塑性模型。

在【模型类型】中选择【塑性-von Mi-ses】，并输入下面的应力-应变特性：【弹性模量】为2.2e11N/m^2，【泊松比】为0.3，【屈服强度】为2.2e8N/m^2，【相切模量】为4e10N/m^2。设置硬化因子为0，如图12-3所示。

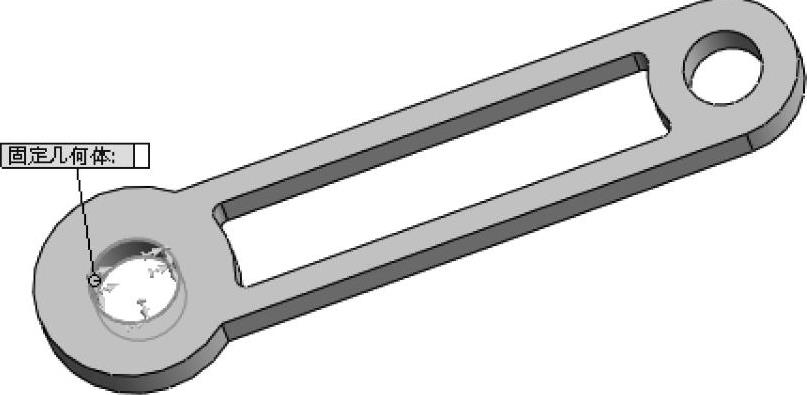
图12-2 添加约束

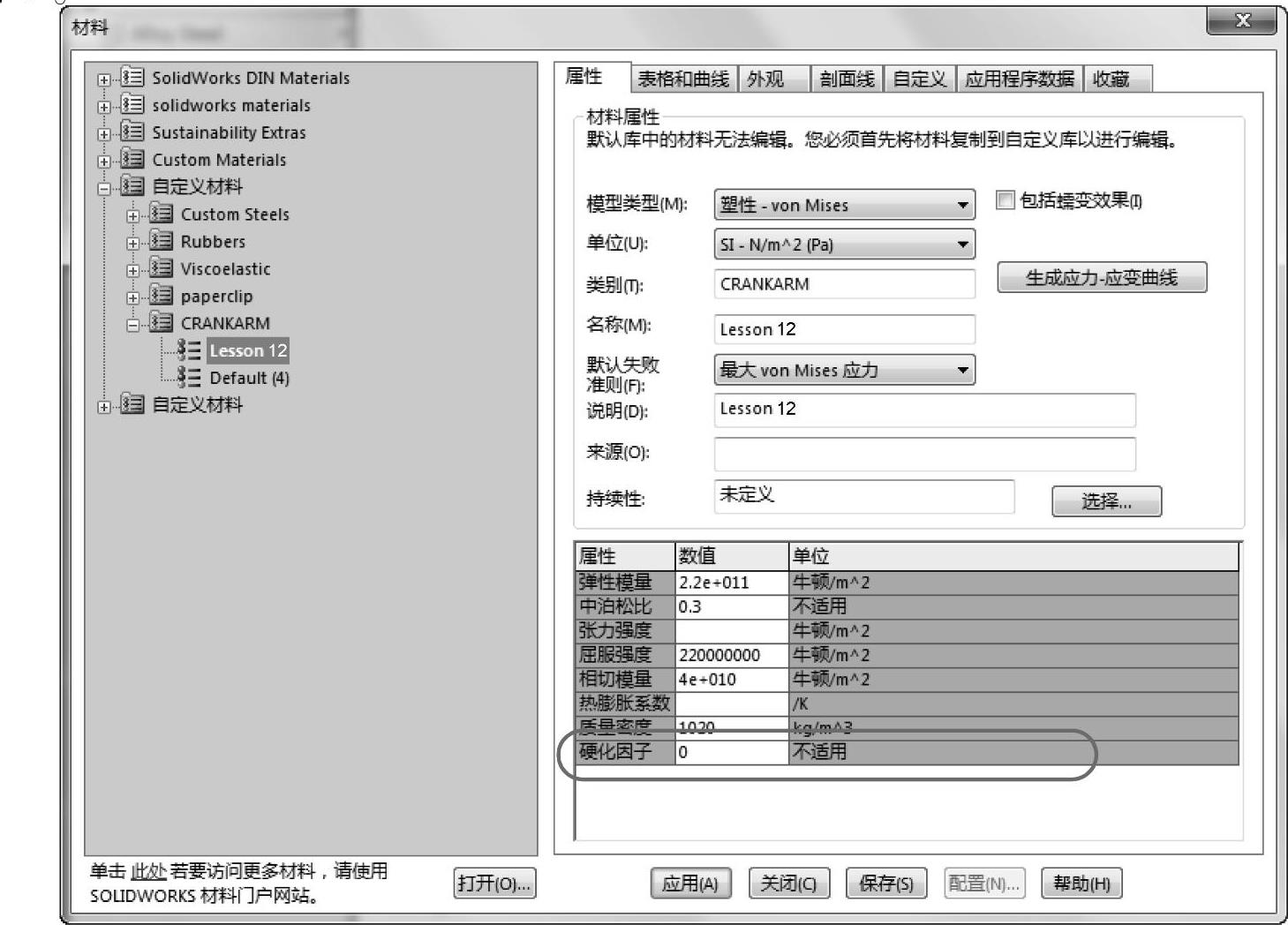
图12-3 应用材料

提示

硬化因子RK=0对应采用各向同性硬化规律的情况。

步骤5 添加第一个力

在半个圆柱面上，按给定方向添加一个大小为11000N的力，如图12-4所示。

在【随时间变化】选项组中，单击【曲线】按钮，然后再单击【编辑】。在【时间曲线】对话框中，指定下面的点来表示分析过程中11000N力的变化：[0，0]，[1，1]，[2，0]，[4，0]，如图12-5所示。

图12-4 添加力（1）

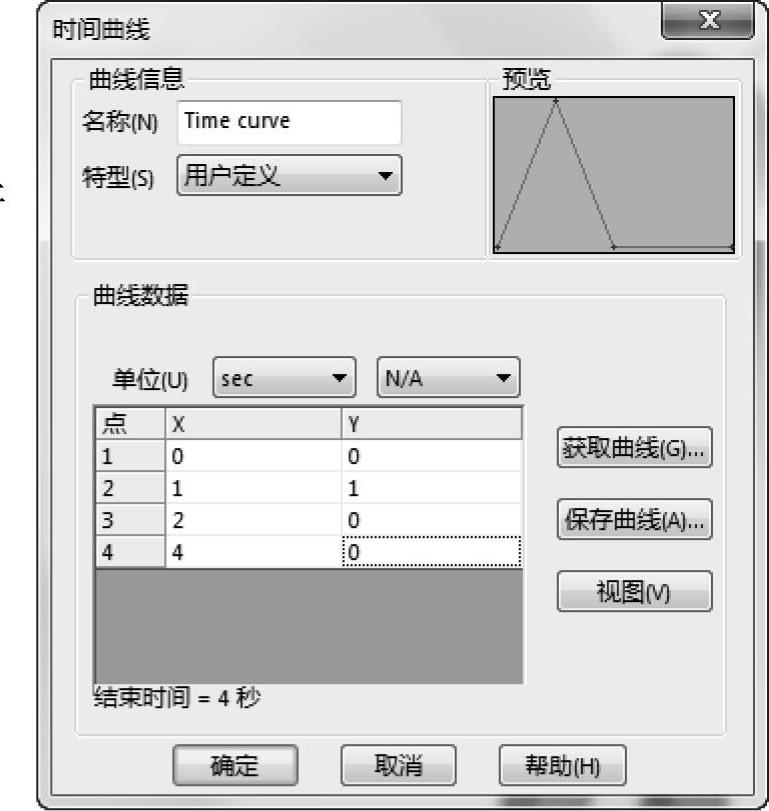
图12-5 时间曲线（1）

步骤6 添加第二个力

在相对的半圆柱面上，在相反的方向添加一个大小为11000N的力，如图12-6所示。

使用下面的点：[0，0]，[2，0]，[3，1]，[4，0]设置力的时间曲线，如图12-7所示。

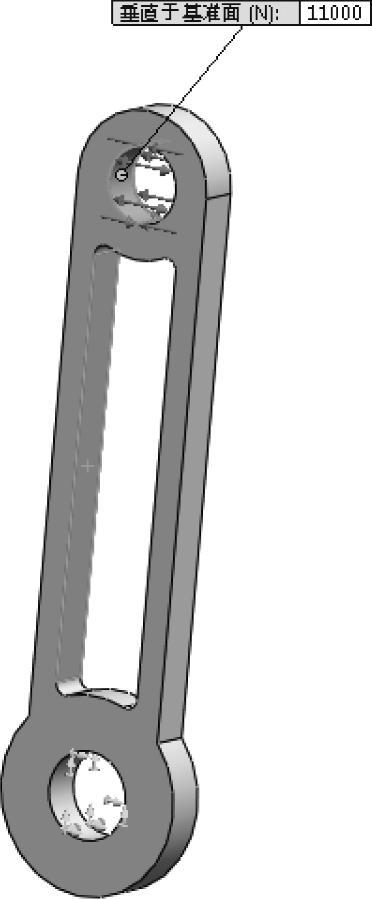
图12-6 添加力（2）(www.xing528.com)

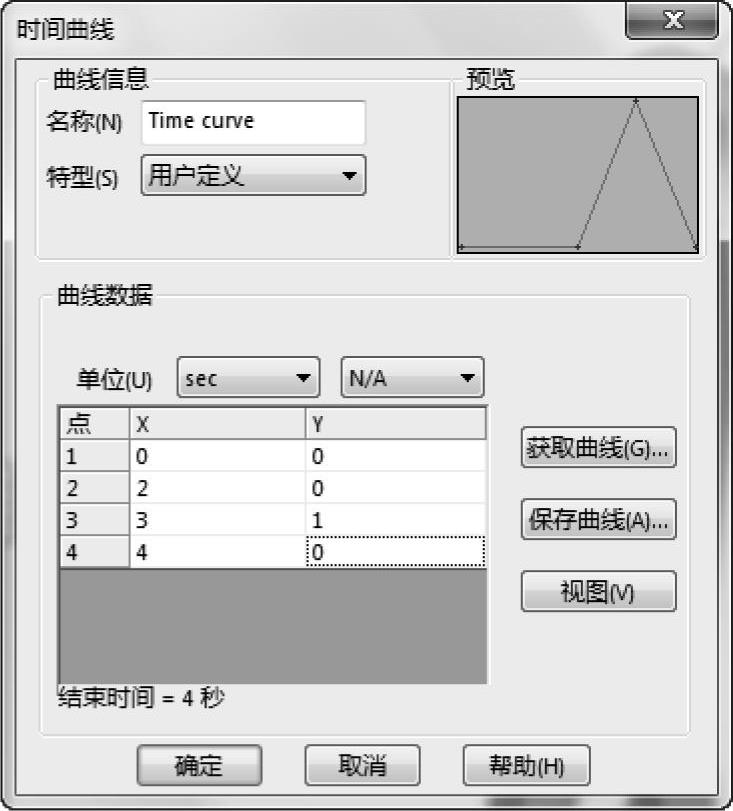
图12-7 时间曲线（2）

步骤7 设置非线性算例属性

右键单击算例Isotropic并选择【属性】，设置非线性分析的选项。设置【结束时间】为4，【初始时间增量】为0.01，【最大】为0.2。确认勾选了【使用大型位移公式】复选框。使用【Intel Direct Sparse】解算器，如图12-8所示。

步骤8 设置高级选项

单击【高级选项】按钮。【控制】方法选为【力】，【迭代方法】为【NR（牛顿拉夫森）】。单击【确定】，如图12-9所示。

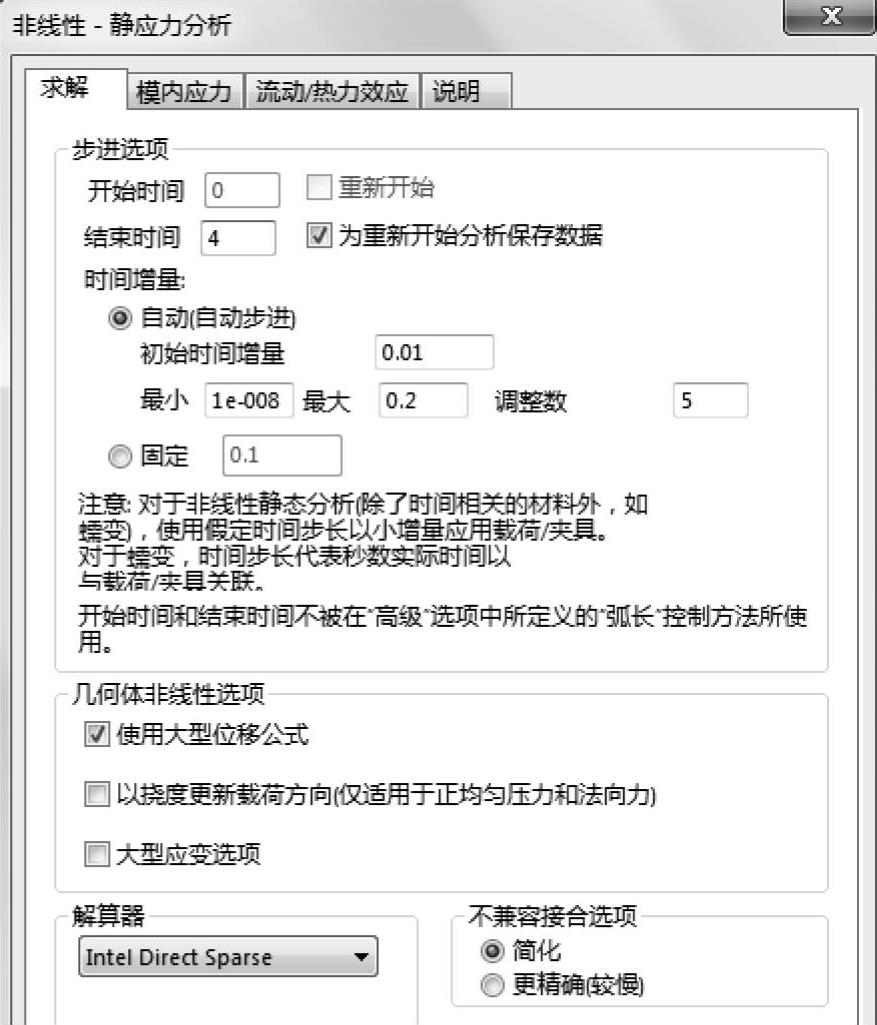
图12-8 设置非线性算例属性

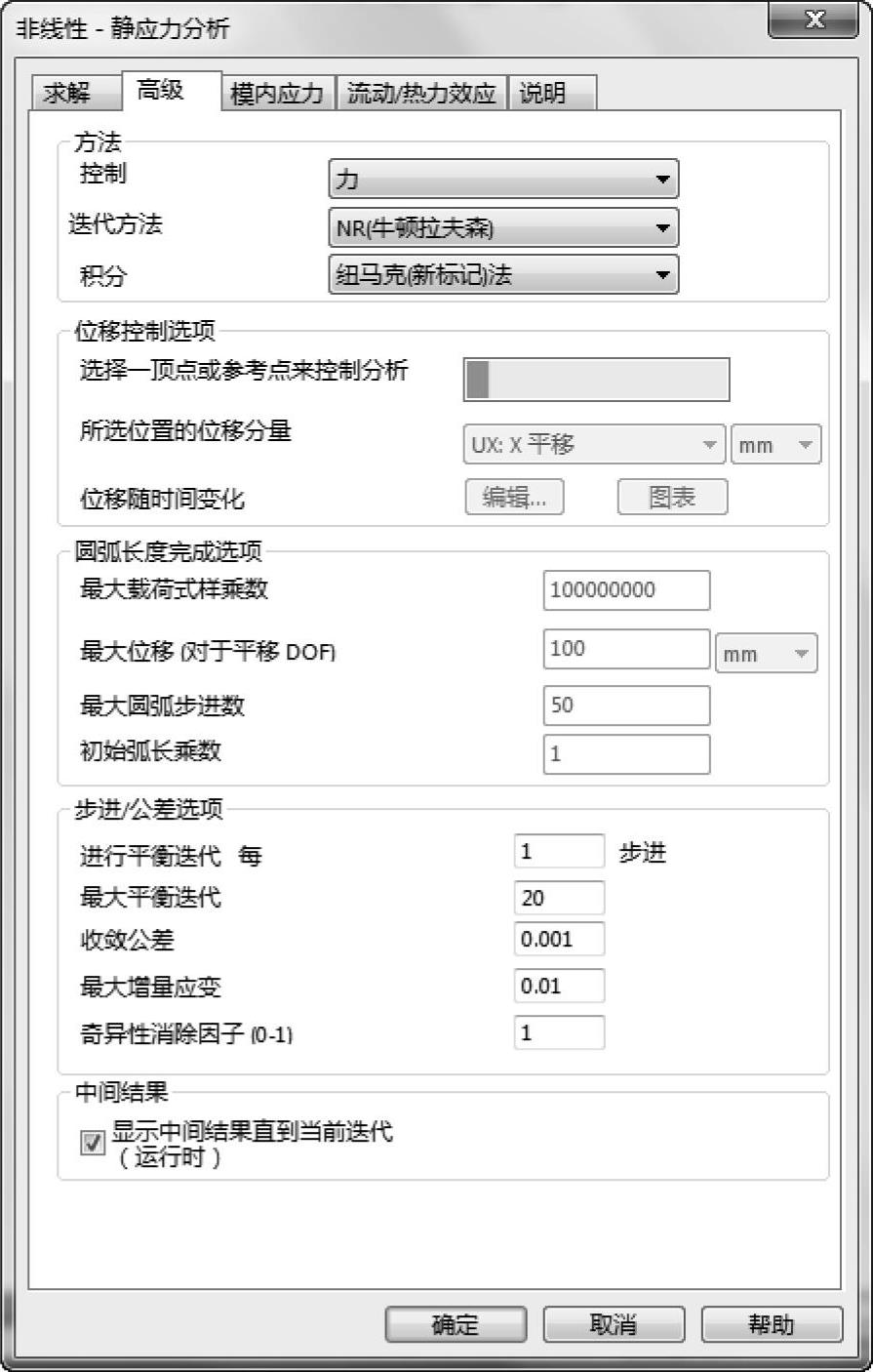
图12-9 设置高级选项

步骤9 设置响应选项

右键单击【结果选项】并选择【定义/编辑】。注意，在靠近曲柄顶部的圆形开口的上部已经设定了一个传感器（图12-10），将使用该传感器来图解显示这个位置的位移。

在【保存结果】选项组中，选择【对于所有解算步骤】。在【响应图解】选项组中，选择之前定义好的传感器Workflow Sensitive1，单击【确定】。

步骤10 生成网格

使用默认的网格参数【整体大小】4.08mm生成【草稿品质网格】，使用【标准网格】，单击【确定】。

步骤11 运行算例

分析将顺利完成。

步骤12 图解显示合位移

图12-10 传感器

在分析结束时刻（t=4）图解显示【URES：合位移】。设置【单位】为mm，【变形形状】为【真实比例】。最后的时间步长图解（如图12-11所示）显示了加载、卸载、反向加载，最终反向卸载之后的永久塑性结果。

步骤13 预先设定顶点的图解响应

右键单击【结果】文件夹并选择【定义时间历史图解】。在【Y轴】中指定为【位移】，【零部件】设定为【UX：X位移】，【单位】设定为mm。如图12-12所示为分析过程中【UX：X位移】的变化。

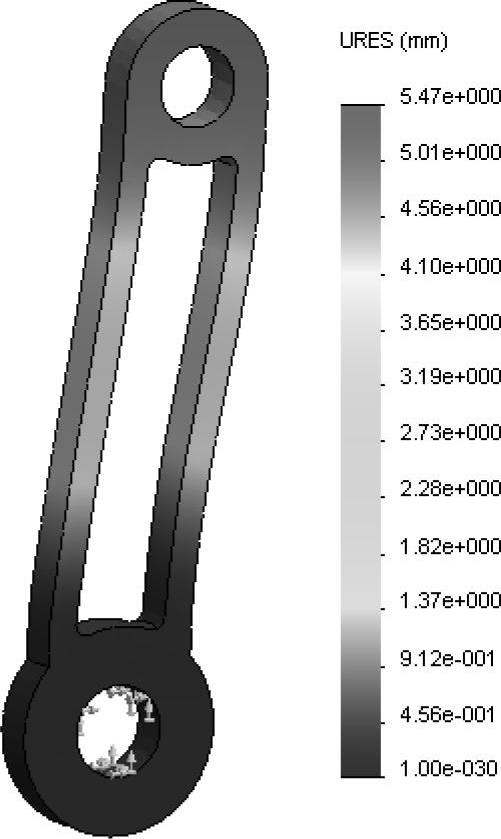
图12-11 位移结果

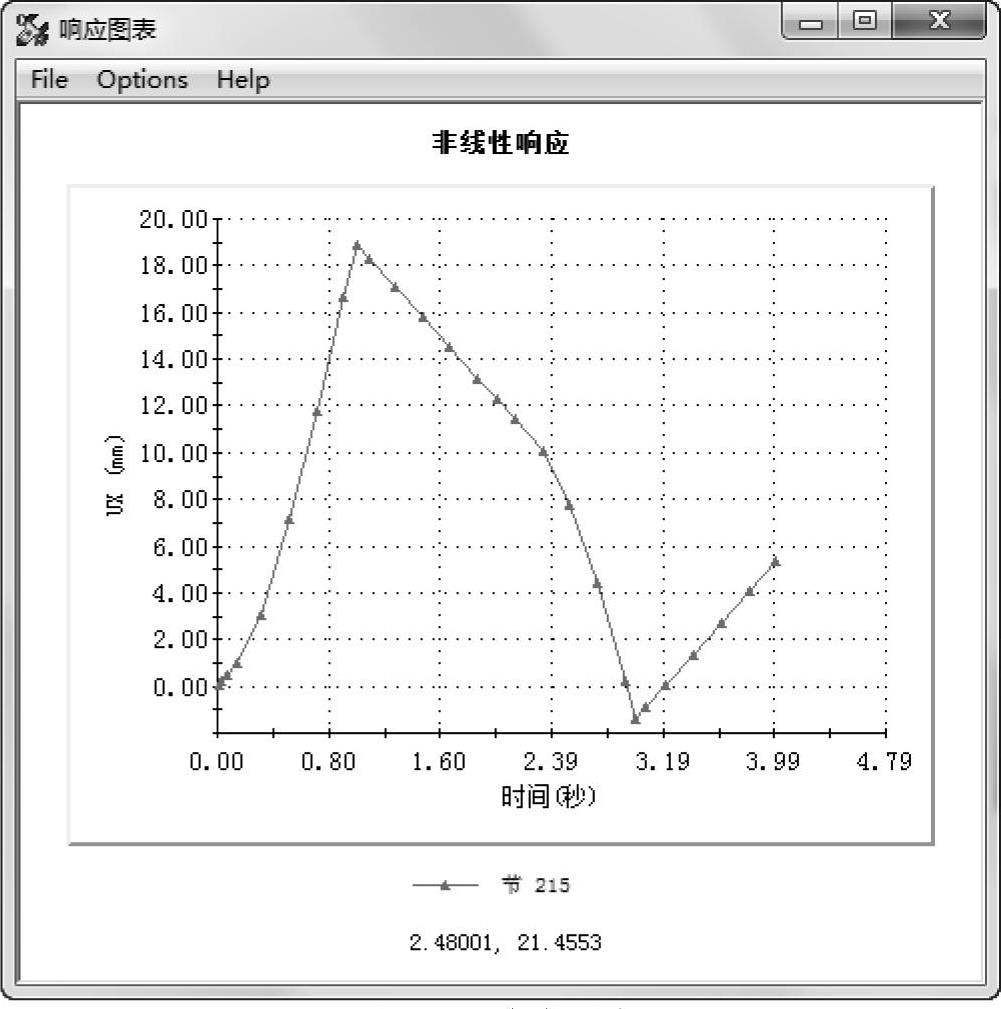
图12-12 响应图表

我们观察到，UX位移的最大值出现在t=1时刻。在t=2时刻，当载荷为零时，位移仍然有12mm。随着在反方向增加载荷，位移会持续减小到t=3时刻，即反方向载荷完全加载时。在本例中，UX位移达到1.5mm。当反向载荷完全移除时（在t=4时刻），UX位移固定在5.56mm处，这是一个永久变形，除非再添加额外的载荷。