如何应用Tresca模型进行非线性分析？

描述弹塑性的理论塑性模型有很多。在本章中，练习的是von Mises和Tresca模型，这两个模型特别适用于金属及其合金，这可以从众多实验和出版物中得到验证。VonMises模型是一个工业标准，被分析师广泛使用于涉及金属及其合金的案例中。建议用户使用VonMises模型作为默认的针对金属的塑性模型，只有当实验确认某些金属适用于Tresca模型时才会使用它（假定可以提供这样的信息）。

本章接下来将使用Tresca塑性模型来求解该问题，这部分内容适用于对这个主题具有更深入兴趣的用户。我们将对比并讨论两个非线性算例的结果。操作步骤

步骤1 为Tresca模型创建新的非线性算例

复制Nonlinear-von Mises算例，重命名为Nonlinear-Tresca，唯一的修改就是对材料塑性模型的定义。

步骤2 编辑材料

在Nonlinear Tresca算例的【材料】对话框中，更改【模型类型】为【塑性-Tresca】，如图11-18所示。所有其他材料设置保持不变。

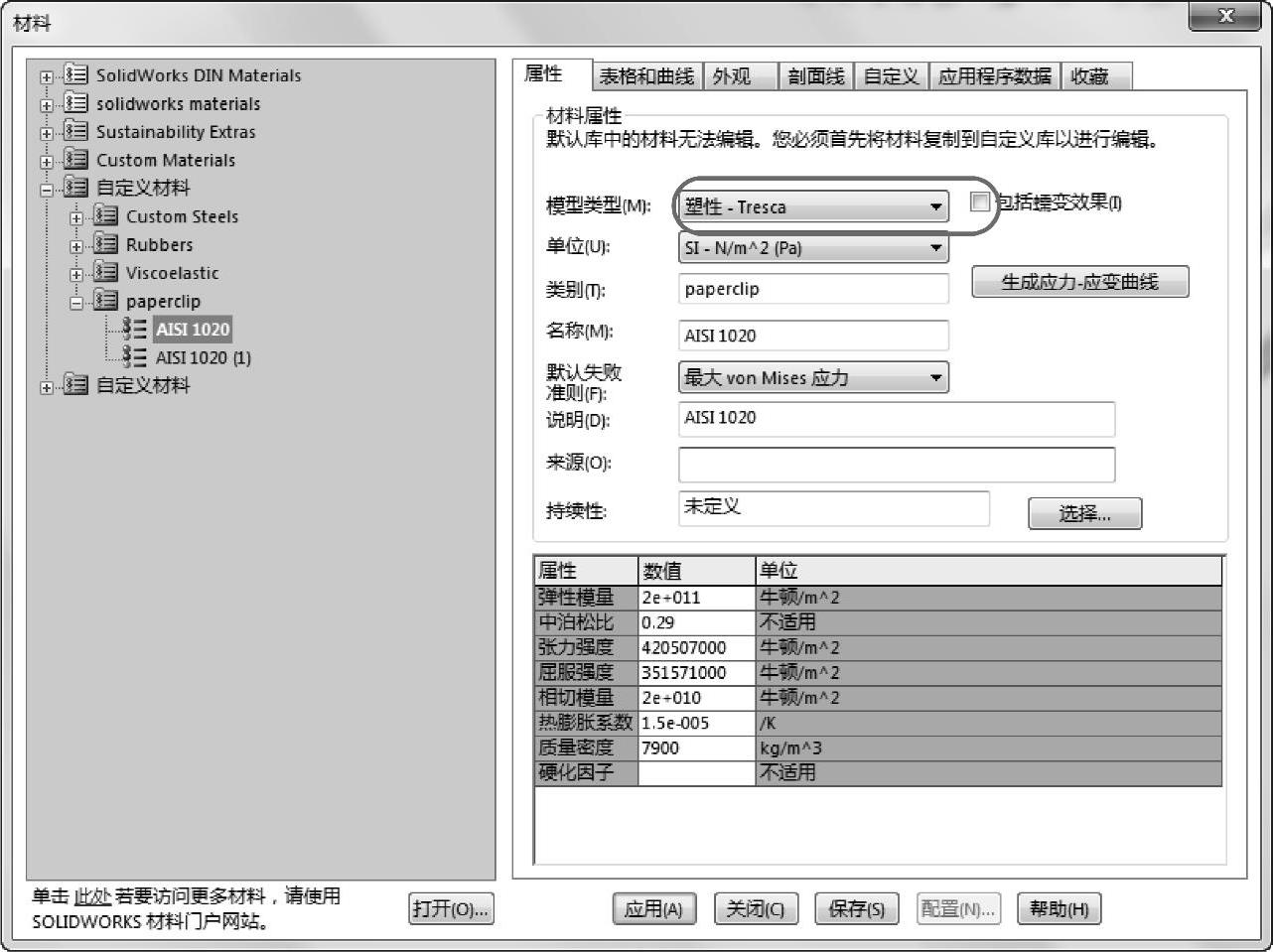
图11-18 编辑材料

步骤3 运行算例

分析将顺利完成。

步骤4 生成t=1时刻的应力图解

在“附录C”中提到，当最大剪切应力（P1-P3）/2等于单向拉伸试验中屈服开始发生的剪切应力（σ_y/2）时，特定材料点的屈服就会发生。为了评估根据Tresca屈服准则的屈服，将图解显示应力强度（P1-P2）的分布。(www.xing528.com)

生成一个新的【INT：应力强度（P1-P3）】图解。设置【单位】为MPa，调节步长【时间】t=1。【变形形状】选择【真实比例】，如图11-19所示。

我们观察到最大应力强度数值大约为427MPa，这要高于材料的屈服强度351MPa，如图11-20所示。

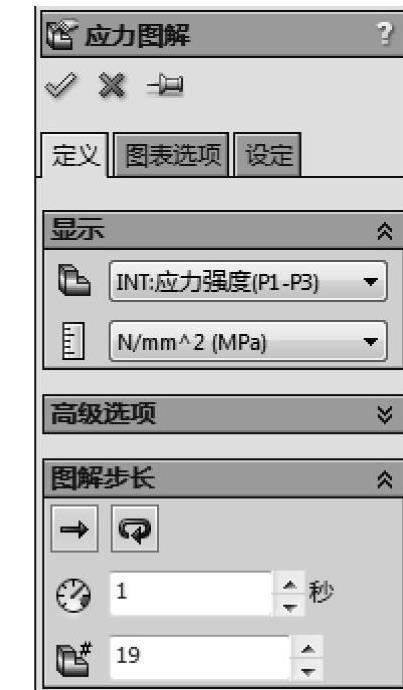
图11-19 设置应力图解

图11-20 应力结果（Tresca应力）

步骤5 图解显示vonMises应力

作为比较，也将图解显示t=1时刻的von Mises应力分布，如图11-21所示。

可以发现，算例Nonlinear Tresca中的von Mises应力组成显示为略小的数值377MPa。和最大应力强度值427MPa比较而言，这个结果说明有大约13%的差异。这个结果与Tresca模型更加保守的特点相符，它比von Mises模型预测的响应偏软。

图11-21 应力结果（vonMises应力）