因为材料在一些区域发生了屈服，因此将使用弹塑性模型，并使用大型位移非线性分析来求解这个模型。此外，非线性算例可以解释发生在模型中的大型位移。操作步骤
步骤1 新建非线性算例
新建名为Nonlinear von-Mises的算例，选择分析【类型】为【非线性】。
步骤2 复制材料
从算例Linear中复制实体文件夹并粘贴到算例Nonlinearvon-Mises的相同文件夹中。
步骤3 修改材料
在Simulation分析树中右键单击paperclip图标并选择【应用/编辑材料】，如图11-6所示。
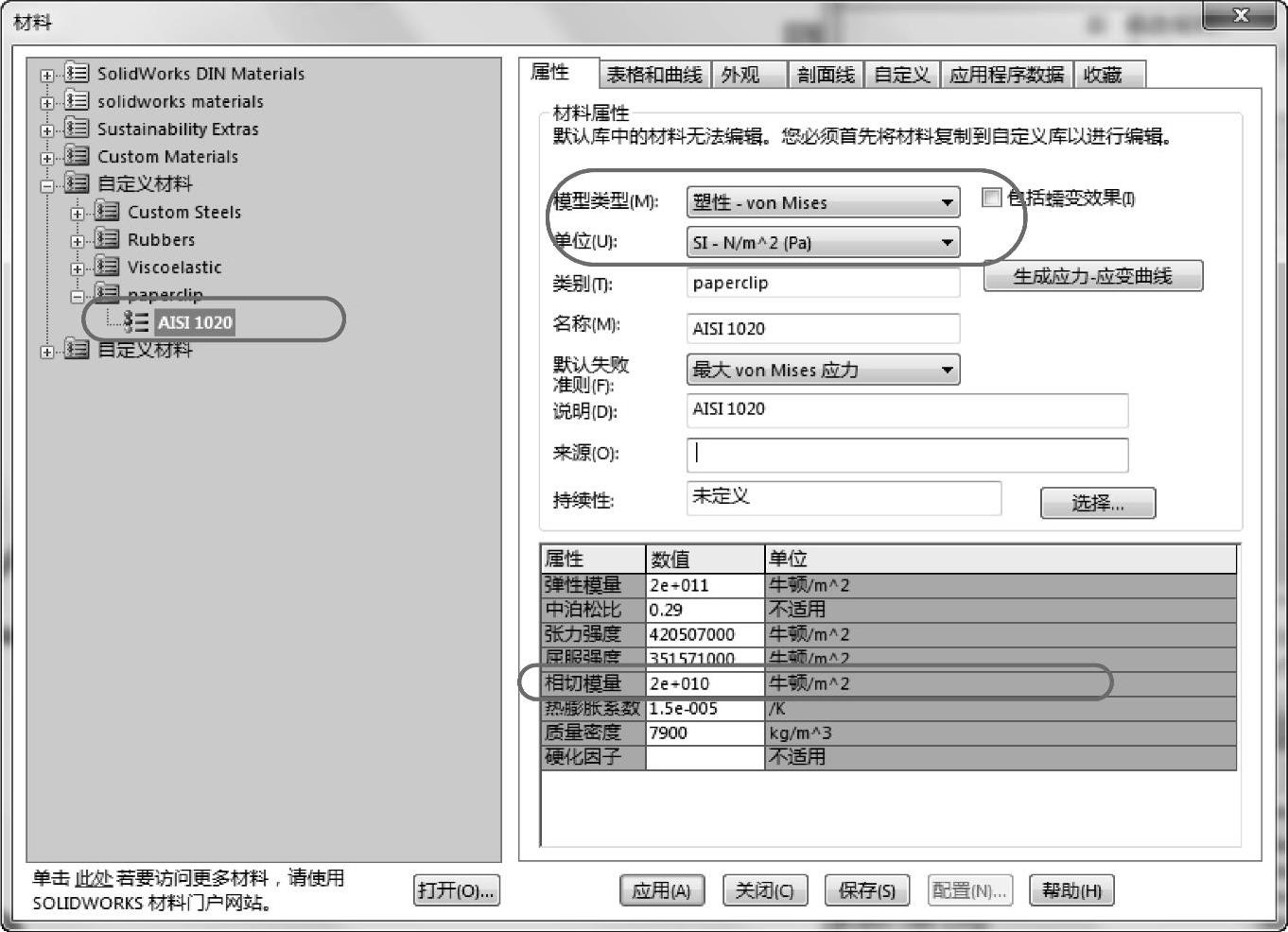
图11-6 修改材料
将AISI1020钢这个材料复制到自定义材料目录下。【模型类型】中选择【塑性-vonMi- ses】，【单位】设定为SI。在【相切模量】中输入2e10N/m^2，即线性弹性模量的10%。单击【应用】后单击【关闭】保存设置。
提示
真实的应力-应变单向材料曲线可以通过双线性曲线逼近。
步骤4 复制算例属性
从算例Linear中拖拽夹具、外部载荷和网格到非线性算例Nonlinear von-Mises中。
提示
除了对比在完全载荷下的最大合位移之外，还想研究卸载载荷后的永久变形。因此，必须重新定义【力/扭矩】的边界条件。
步骤5 修改加载和卸载的力
右键单击Force-1并选择【编辑定义】。在【随时间变化】选项组中，选择【曲线】，然后再单击【编辑】按钮，如图11-7所示。在【曲线信息】选项组中更改【名称】为Load-Unload。在【曲线数据】对话框中输入下列点：[0，0]，[1，1]和[2，0]。指定的两个斜线函数代表分析过程中力的变化，如图11-8所示。
图11-7 修改力
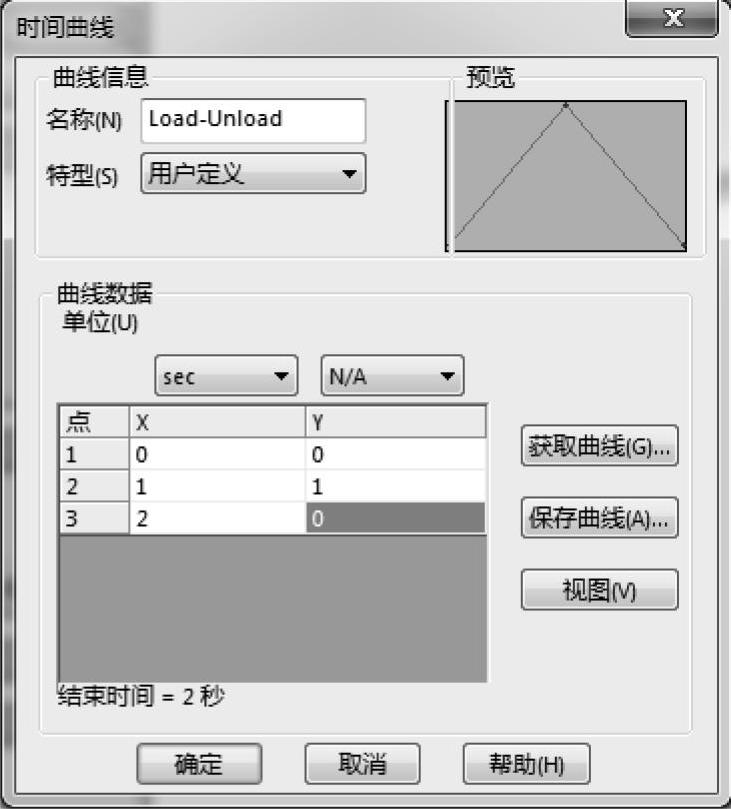
图11-8 编辑时间曲线
提示
要新添一行数据，只需双击【曲线数据】对话框中【点】
行的数字3单元格。同时，注意到这条曲线还要乘以力定义的数值（1N）。
单击【确定】接受【时间曲线】的编辑，单击【确定】保存力Force-1修改。
步骤6 设置算例Nonlinearvon-Mises的属性
【结束时间】：2；【初始时间增量】：0.01；【最小】时间增量：1e-8；【最大】时间增量：0.1；保留【调整数】为5；【开始时间】等于默认值0；在【几何非线性选项】选项组中，勾选【使用大型位移公式】复选框，并选择【解算器】为【Direct sparse解算器】，如图11-9所示。
步骤7 设置高级选项
单击【高级选项】，在【方法】选项组中选择了【力】控制和【NR（牛顿拉夫森）】迭代方法。保留其他所有设置为默认值。单击【确定】，如图11-10所示。
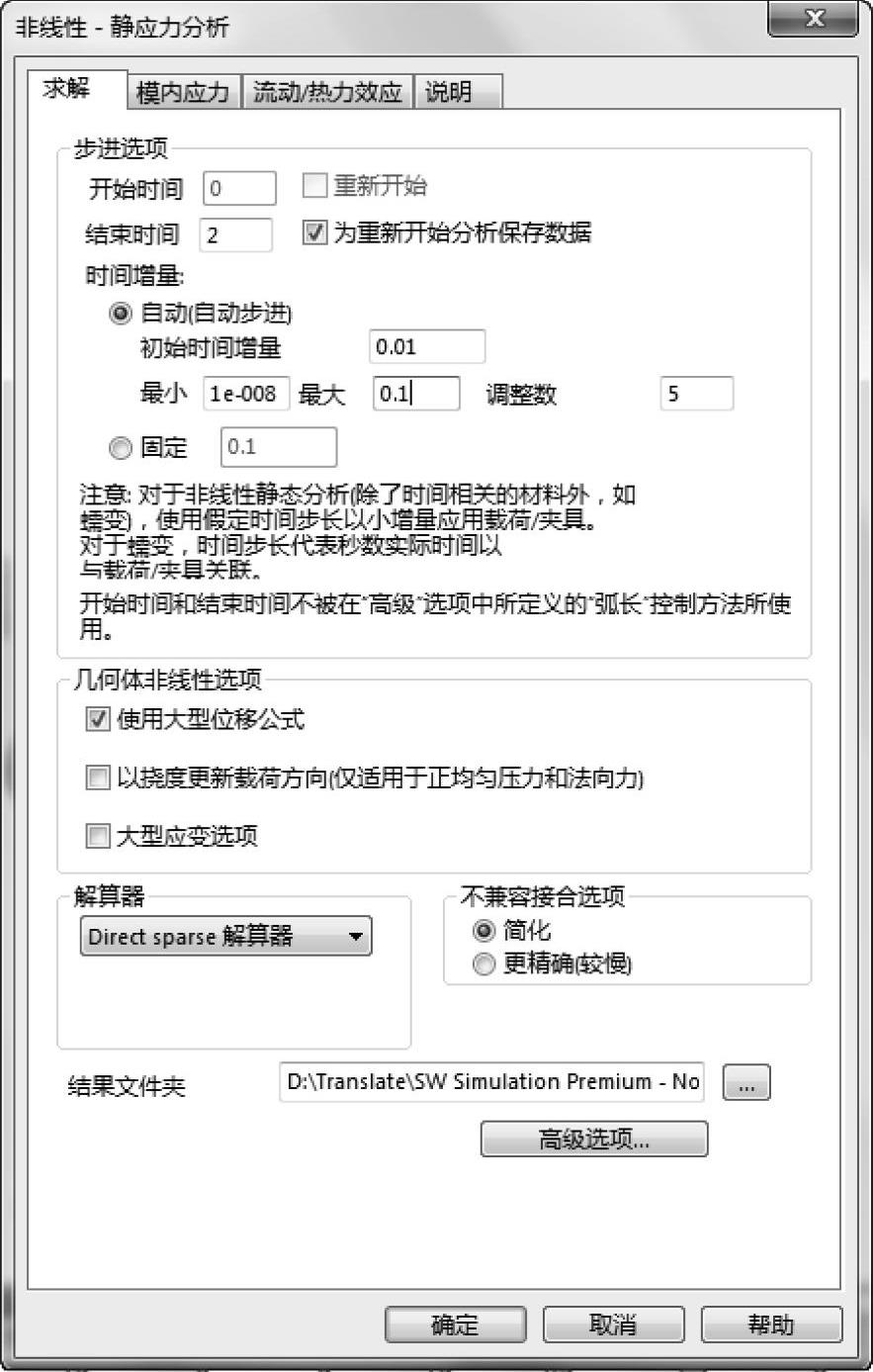
图11-9 设置算例属性
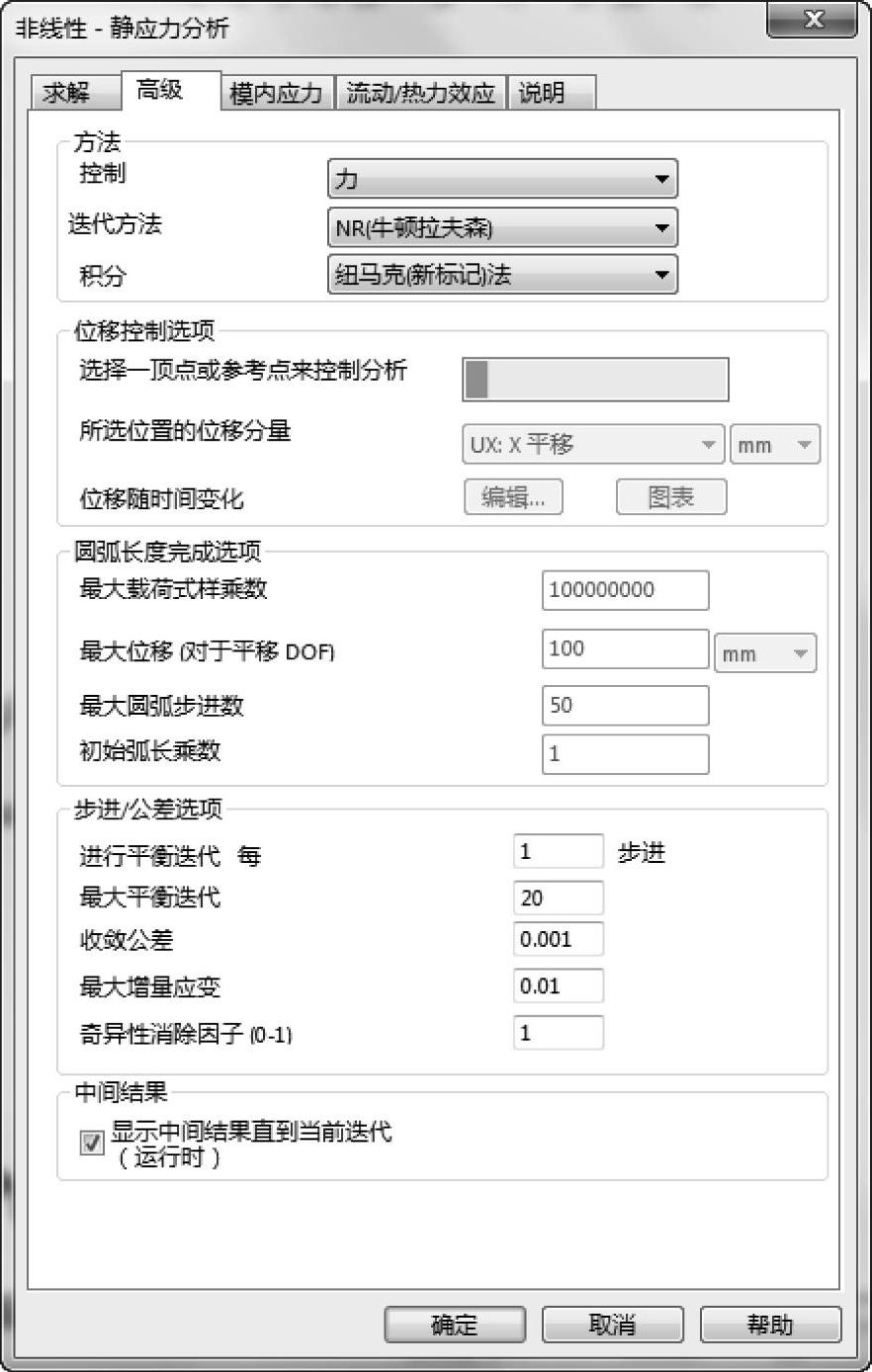
图11-10 设置高级选项(www.xing528.com)
步骤8 运行算例
分析将顺利完成。
步骤9 在t=1时刻生成应力图解
生成时间t=1时刻的【VON：von Mises应力】图解。这个时刻对应着作用力完全加载的时间点。设置图解的【单位】为MPa，【变形形状】为【真实比例】（1∶1），如图11-11所示。
图11-11 图解应力结果（1）
可以观察到最大的von Mises应力386.88MPa远低于线性算例对应的数值。这是因为材料在屈服后变得更软。也就是说，双线性应力-应变曲线在屈服之后更加平缓（ETAN等于杨氏模量的10%）。
步骤10 生成t=1时刻的位移图解
生成时间t=1时刻的【URES：合位移】图解。设置【单位】为mm，【变形形状】为【真实比例】，如图11-12所示。
可以观察到在t=1（t=1时载荷最大）时的最大合位移为21mm，这远大于从线性算例中得到的结果（最大的URES=16.4mm）。这是由于模型的局部区域受到塑性变形而导致材料变软。
步骤11 图解显示t=2时刻的vonMises应力
在t=2时载荷已经完全移除，然而由于发生永久变形，会看到一定程度的残留应力和永久变形。最终图解显示如图11-13所示。
图11-12 图解位移结果（1）
图11-13 图解应力结果（2）
纸夹的最大残留Von Mises应力为121MPa。
步骤12 图解显示t=2时刻的合位移
最大永久合位移大约为6.3mm，如图11-14所示。
步骤13 探测位移图解
探测纸夹顶部附近的节点（图11-15），然后单击【响应】按钮，如图11-16所示。
图11-14 图解位移结果（2）
图11-15 探测结果
步骤14 查看图解
如图11-17所示，响应图表显示分析过程中合位移的变化，观察到分析结束时的永久变形量为6.5mm。
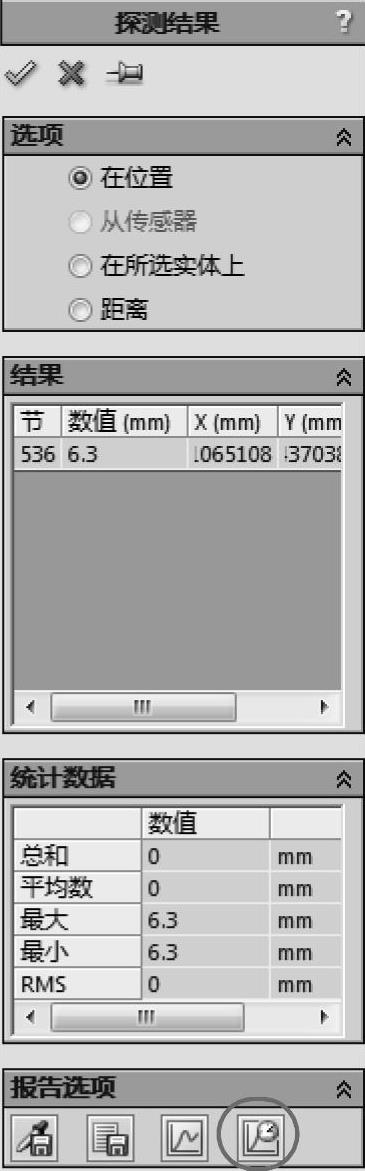
图11-16 探测位移图解
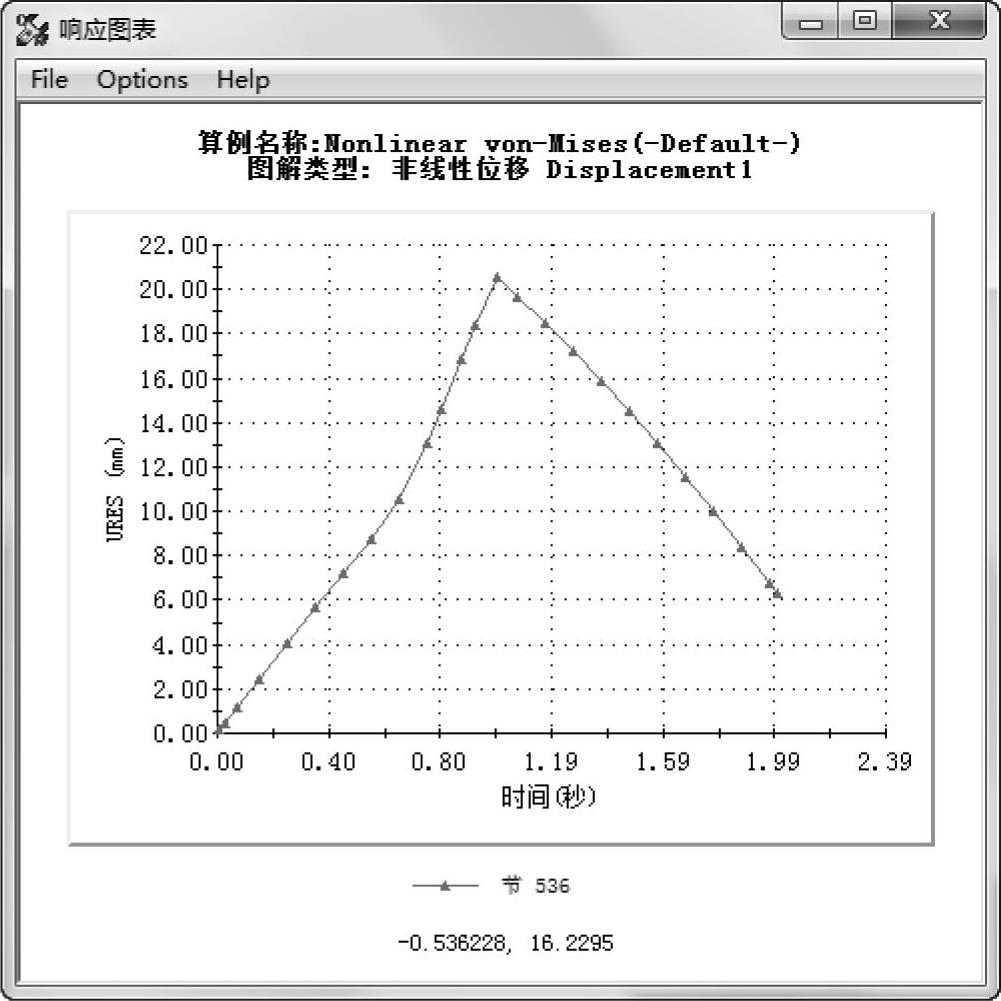
图11-17 响应图表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
