在本次分析中,我们:
1.选择____控制方法。
2.对____选择这种控制方法和____控制方法,因为在非线性求解中得到的平衡路径显示了____和____点。这两种控制方法在这两个点都无法收敛。
3.线性屈曲一般会(高估/低估)载荷因子。
4.非对称屈曲和对称屈曲比较而言,可得到(更小/更大)的载荷因子值。
5.在设计中(会/不会)考虑非对称屈曲。
练习 架子的非线性分析
在本练习中,将对一个架子进行一次屈曲分析。
本练习将应用以下技术:
● 线性屈曲。
● 非线性非对称屈曲。
● 弧长:参数。
1.问题描述 架子的结构包含两个中间隔板和两个端部,并且固定在底端。每层隔板(自上而下)分别受到45N、90N和440N的载荷,如图10-25所示。
我们要分析架子的最高von Mises应力、最大位移以及在分析中加载书和其他出版物时的屈曲安全系数。首先,需要运行线性静应力分析和屈曲分析,以快速评估结构性能和稳定性。然后,将采用非线性算例来求解相同的问题。因为屈曲现象是预料之中的(相对薄的结构受到压缩载荷),我们会使用弧长控制方法。最后还将对比和讨论线性和非线性的结果。
装配体模型包含四个钣金零件,并使用壳单元划分网格。对应中间隔板的零件被使用了两次(两个实体Plate3)。装配体中的所有零件材料都是合金钢。
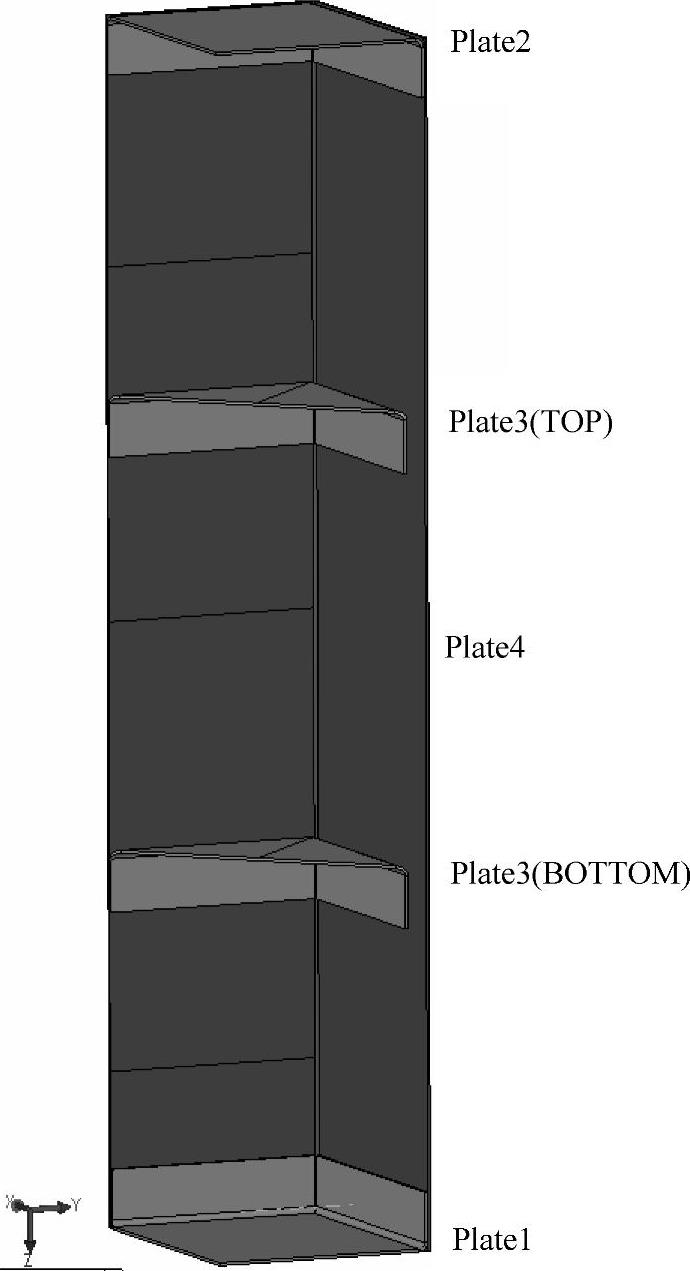
图10-25 架子
操作步骤
步骤1 打开装配体文件
打开Lesson10\Exercises文件夹下的文件shelf。
步骤2 新建算例
新建【静应力分析】算例并命名为Static Stress。
步骤3 应用材料
对零件文件夹下的所有壳体应用合金钢的材料。
步骤4 添加夹具
对底层隔板(Plate1)的底面添加【固定几何体】夹具,如图10-26所示。
步骤5 添加力
对架子各层的表面分别指定大小为45N、180N和900N的法向力,如图10-27所示。
步骤6 生成网格
使用默认的数值,【整体大小】为12.6mm,【公差】为0.63mm,选择【标准网格】。
步骤7 运行算例
步骤8 查看应力和位移结果
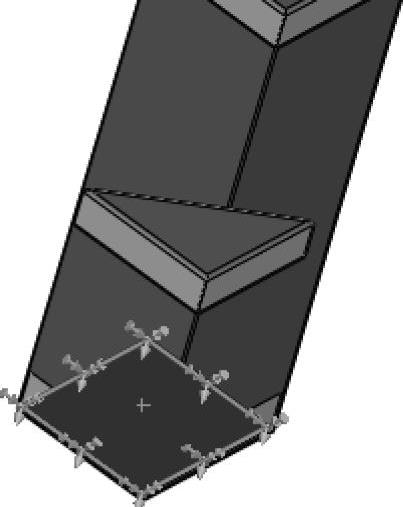
图10-26 添加夹具
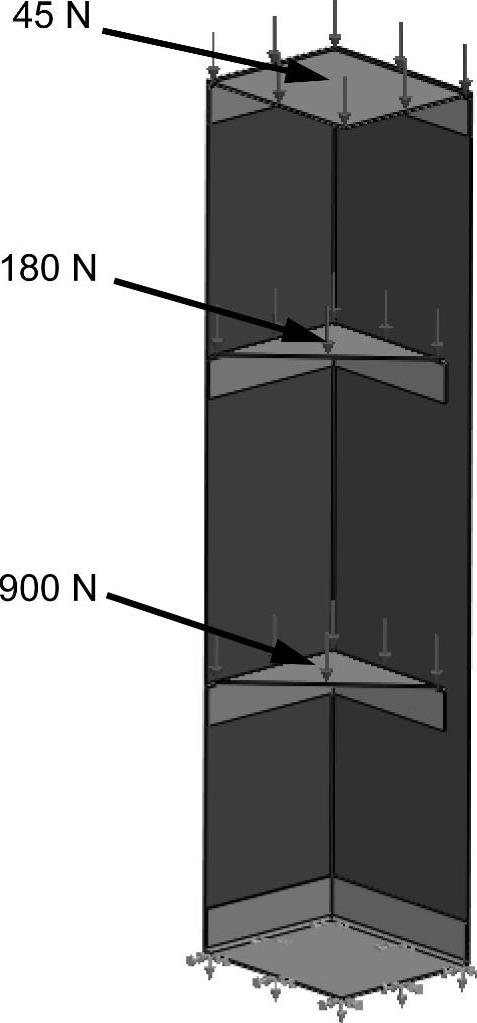
图10-27 添加力
图解显示von Mises应力与合位移,确认【变形形状】设定为【真实比例】,如图10-28所示。
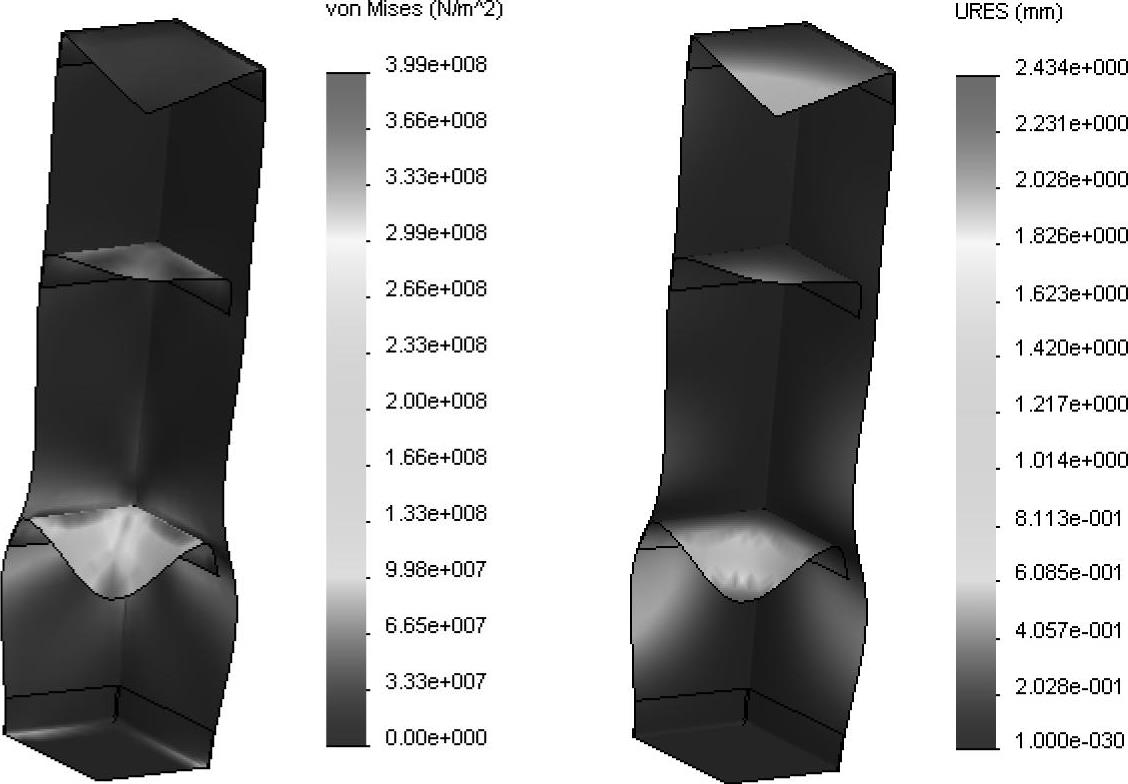
图10-28 查看结果
注意到最大应力小于材料的屈服应力,位移大约为2.4mm。
2.线性屈曲分析 下面将运行一次线性屈曲分析。(https://www.xing528.com)
步骤9 创建新的线性屈曲算例
创建一个新的【屈曲】算例并命名为Linear Buckling。
步骤10 复制算例属性
从静应力分析算例中拖拽零件、夹具、外部载荷和网格到屈曲算例中。
步骤11 运行算例
步骤12 列举屈曲安全系数
观察到屈曲安全系数大于1,也就是说,在屈曲安全系数等于2.71时,根据线性屈曲分析而言我们的结构是安全的,如图10-29所示。
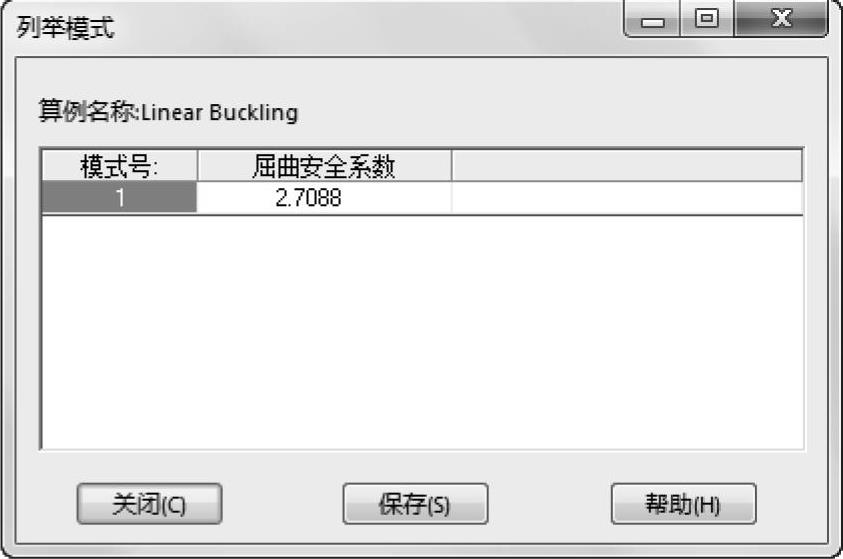
图10-29 列举屈曲安全系数
3.非线性屈曲分析 现在要运行一次非线性分析,这会提供屈曲现象、结构的应力水平以及位移方面更准确的图像。还能对两个线性算例的准确性做更多的评价。
步骤13 新建非线性算例
新建名为Nonlinear Buckling的非线性算例。
步骤14 复制算例属性
从静应力分析算例中拖拽零件、夹具、外部载荷和网格到非线性算例中。查看所有三个隔板的力和各自的时间曲线,因为预测会发生屈曲现象,我们将使用弧长控制方法,而不使用时间曲线。
步骤15 设置结果选项
已经提前创建了一些传感器,用来观察各个位置的结果。
在【结果选项】中,【保存结果】选择【对于所有结算步骤】,【响应图解】选择【Workflow Sensitive1】,如图10-30所示。
步骤16 设置非线性算例的属性
确保【初始时间增量】和【最大】时间增量都设定为合理的数值。确认勾选了【使用大型位移公式】复选框。在【高级】选项卡中,选择【弧长】控制方法,使用“非线性静应力屈曲分析”这一章的公式,计算【最大位移(对于平移DOF)】选项中的数值。对【最大圆弧步进数】选项设定合理的数值,使用【Direct sparse解算器】。
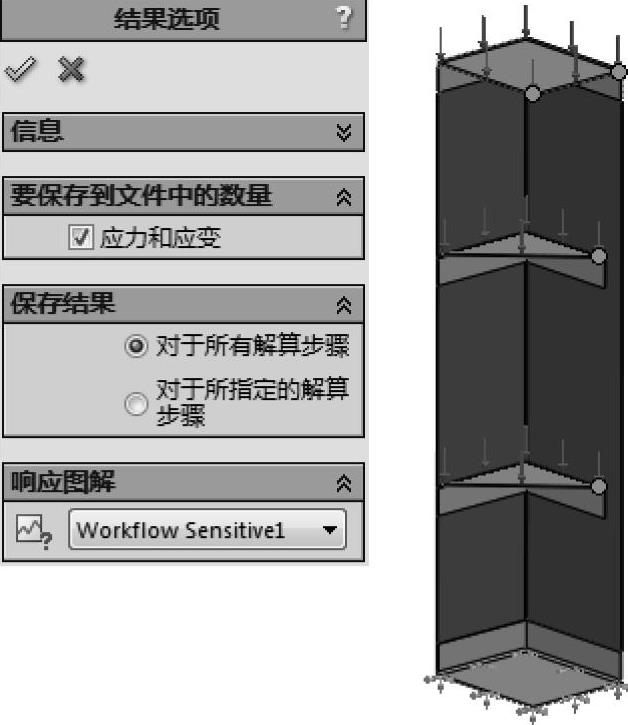
图10-30 设置结果选项
步骤17 运行算例
步骤18 图解显示响应图表
对所选的四个顶点显示响应图解,如图10-31所示。
请注意,如果没有在平衡路径中得到跳跃点,则必须修改弧长方法的设置(也就是【最大圆弧步进数】、【最大位移(对于平移DOF)】、【初始时间增量】和【最大】时间增量),然后重新运行算例。由于无法提前知道极点的位置,初始位置有可能是不理想的,如图10-32所示。
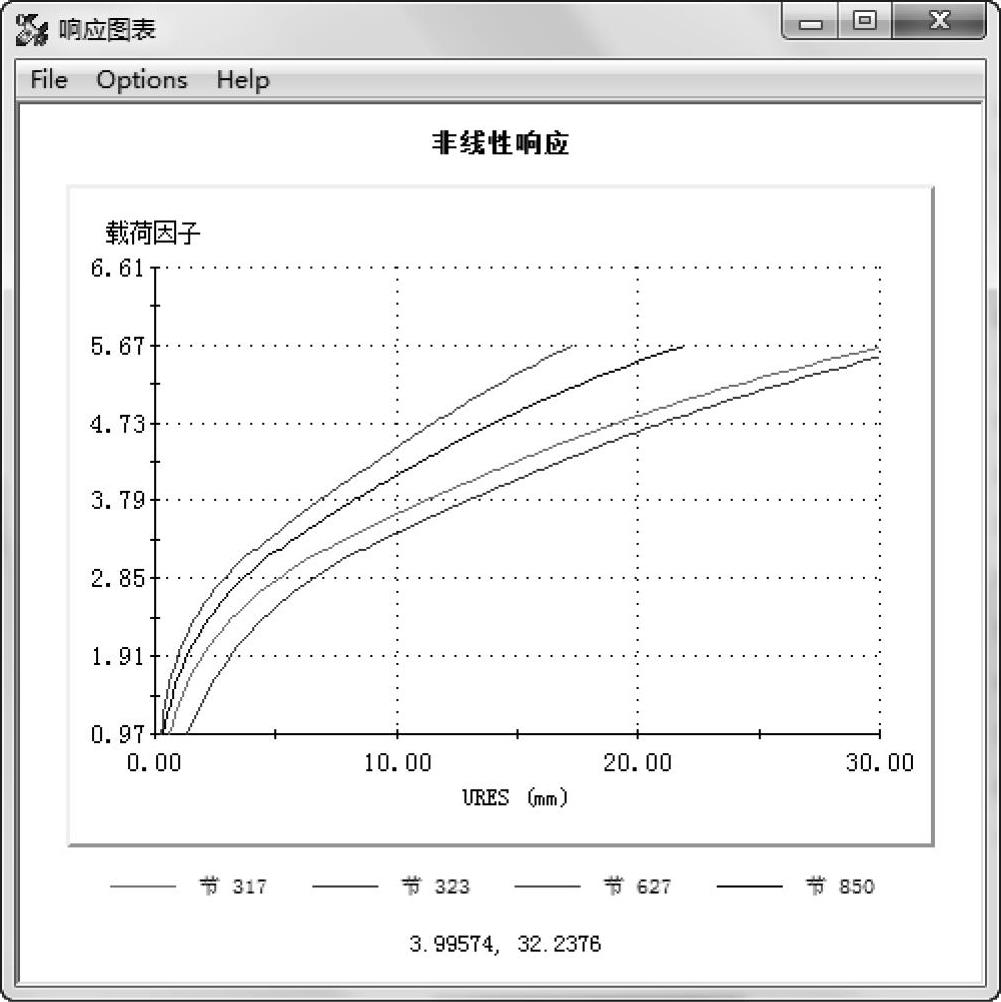
图10-31 响应图表(1)
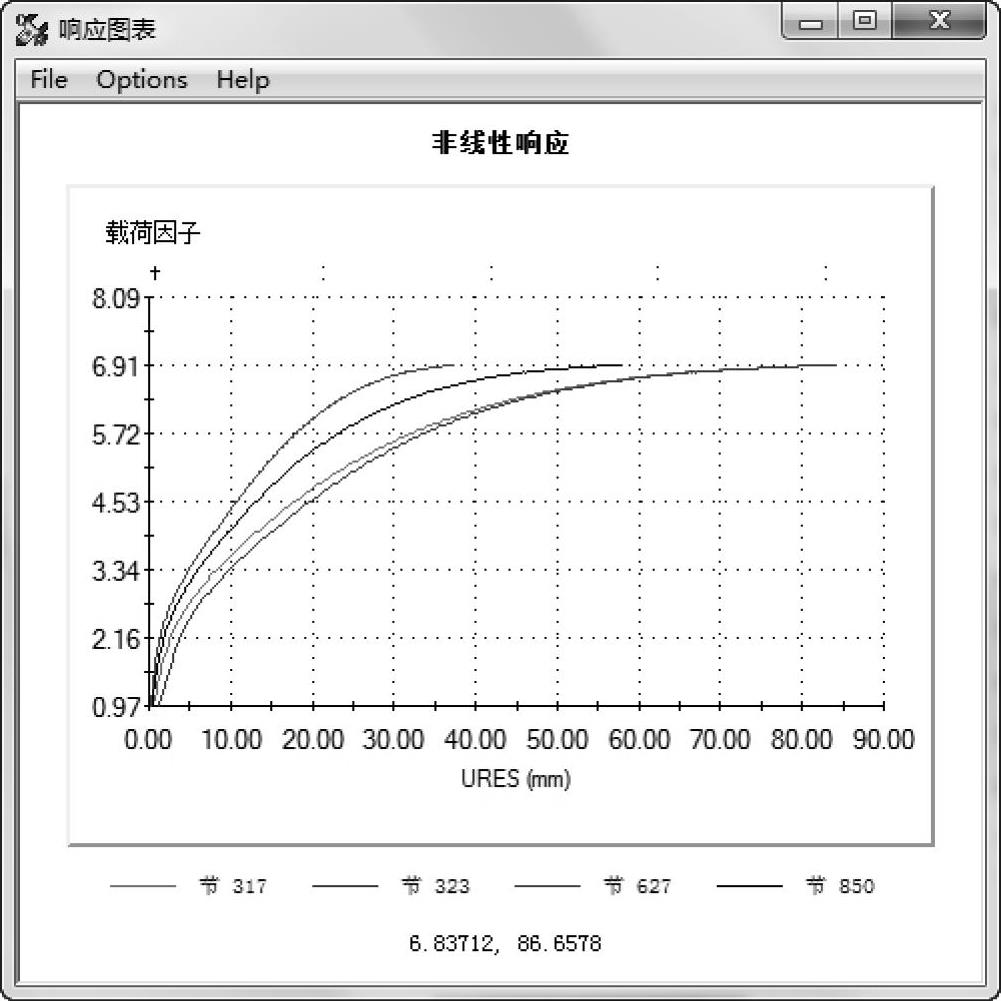
图10-32 响应图表(2)
步骤19 显示载荷因子为1时的应力和合位移(图10-33)
步骤20 图解显示接近分析完成时刻的应力与合位移(图10-34)
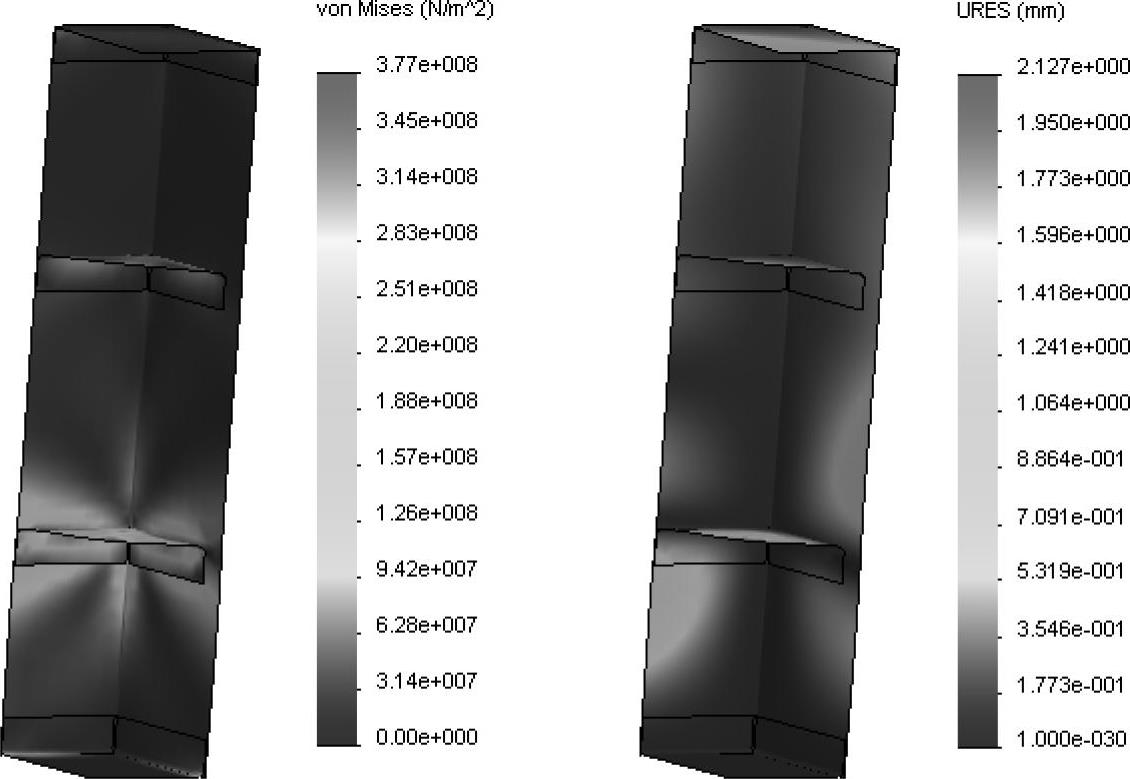
图10-33 显示结果(1)
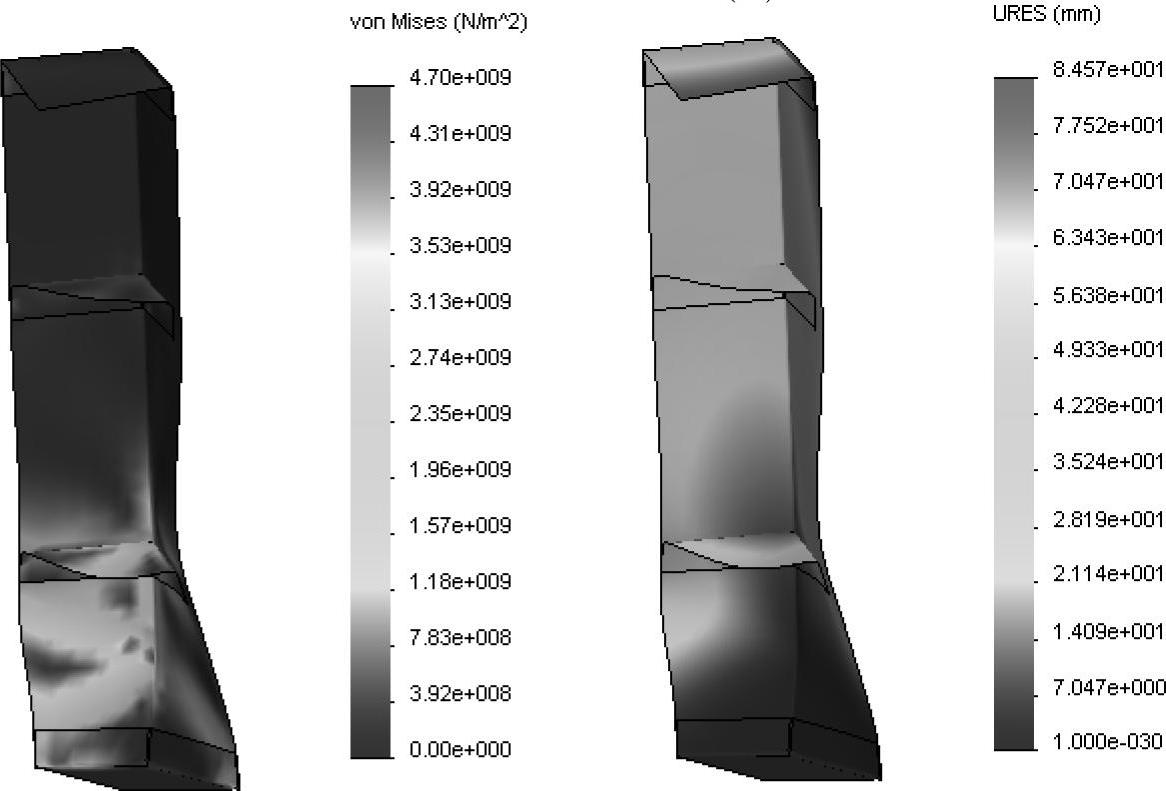
图10-34 显示结果(2)
4.讨论 可以注意到,在这个模型中,载荷因子看上去是持续增加的。有些结构的设计遵循这样的方法:材料的刚度不允许结构轻易发生屈曲,首先可能发生的会是屈服和过度变形。在本模型中,看到架子先发生扭曲,然后再弯曲。在非线性算例中可以看到,载荷因子为1的结果接近于线性算例的结果。然而,随着载荷持续增加,过度的变形和存在于模型中的应力成为首要关注对象,而不再是屈曲。
线性屈曲提供了屈曲载荷的快速评估。因为快速,这些结果也继承了线性分析的先天不足,也就是线性屈曲并不考虑架子变形所产生的刚度变化。对于某些结构(比如柱面壳体),这些局限是不可接受的,这时需要考虑使用非线性的解决方案。
通常情况下,线性屈曲会比非线性分析中得到的屈曲载荷提供更高的估值,因此必须小心处理。然而在一些情况下,线性屈曲的预测可以预示一定载荷下的屈曲,但在实际情况下,结构不会轻易发生屈曲,更多是由于屈服和(或)过度变形而发生的失效。本练习对架子模型的分析也揭示了这一现象。线性屈曲分析预测一定临界载荷下的屈曲,而非线性分析揭示的是更复杂的现象,即当屈服和(或)过度变形导致结构失效时,在更高的载荷作用下会发生明显的刚度下降。
5.总结 在本练习中,我们比较了线性静应力和线性屈曲的估值,并和非线性算例得到的结果进行了对比。观察到非线性屈曲算例准确地描述了模型的特性,因为线性屈曲算例没有按可以接受的准确度来描述特性,是由于没有考虑到变形过程中的刚度变化。然而,一般来说,线性屈曲结果通常都需要谨慎对待,因为它们可能会明显高估载荷因子。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




