电路板疲劳评估练习

在本练习中，将基于随机振动的结果，计算电路板的疲劳评估。

项目描述 在本练习中，外壳固定在相同位置，其货柜受到Y方向的相同激发（标准MIL-STD_-810G，方法514.5需要材料沿三个正交的方向激发和分析）。执行和练习5-1中相同的方法，分析Y方向的激发，且合成的PSD曲线存储在文件夹Lesson05\Exercises中。

这个练习的目标是确定在3σ的输出水平下电子元器件的疲劳强度。

操作步骤

步骤1 打开装配体文件

打开文件夹Lesson05\Exercises\Fatigue of Circuit Board下的文件“Electronic_Assem-bly”。

步骤2 查看随机激发

查看应用在Y方向的PSD加速度激发。使用和第5章相同的分析获取这条曲线，如图5-49所示。

提示

存储在文件夹Fatigue of Circuit Board中的PSDacceleration Y.csv文档包含本数据。

步骤3 求解随机振动仿真

按照前面练习的步骤3至步骤9，完成这个随机振动仿真。在算例属性中，指定【频率点数】为20。

图5-49 编辑曲线

步骤4 RMS结果

图解显示Y方向的位移RMS结果，如图5-50所示。

图5-50 图解显示位移的RMS结果

可以看出Y方向位移的最大RMS（或1σ）数值为1.8e-1mm。

步骤5 PSD响应图表

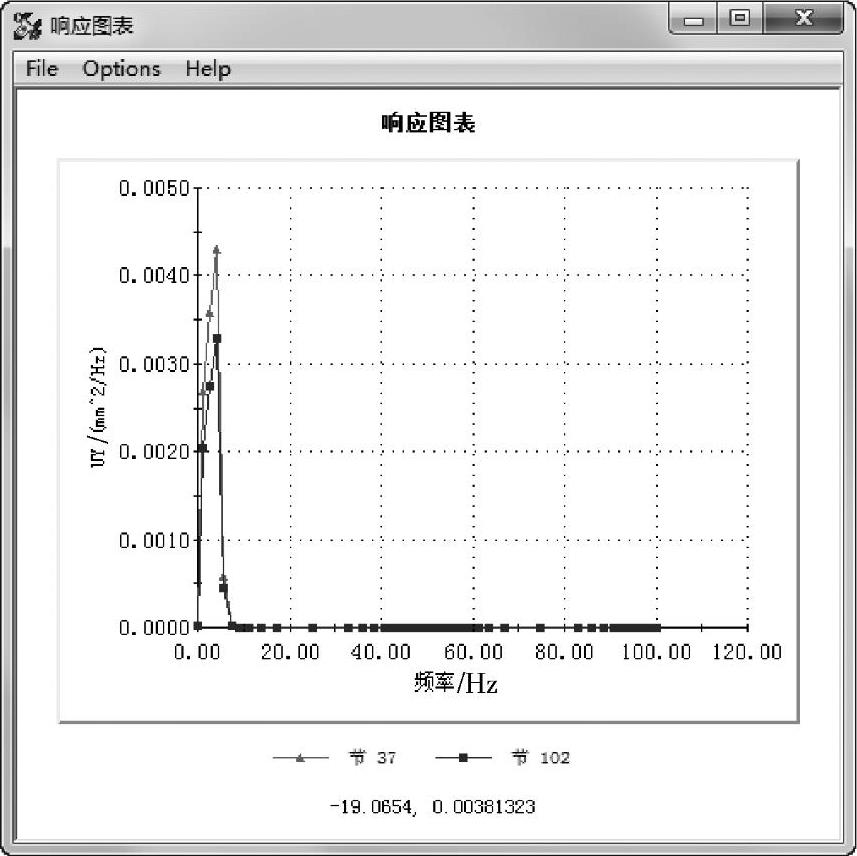
图解显示在两个传感器位置加速度和位移PSD响应图表的Y分量，如图5-51和图5-52所示。

可以看出两条曲线的峰值都出现在4.06Hz附近，加速度和位移PSD显示的最大值分别为2.79e7（mm/s^2）^2/Hz和3.3e-3mm^2/Hz。可以将加速度的峰值大小与用户限定的范围进行比较，以确定设计是否可以获得通过。一般而言，位移量没有多少用处，只使用加速度波谱。

最重要的结论是，占主导地位的输出振动发生在4.06Hz附近，这个数值将用于疲劳计算中。

(www.xing528.com)

图5-51 响应图表（一）

图5-52 响应图表（二）

电路板的疲劳 在这个练习中，使用来自“VibrationAnalysisforElectronicEquipment byD.S.Stein-berg”的经验公式，根据这篇文章，2000万个周期的3σ限定位移可以由下面的公式计算得出

式中 B——平行于元器件的电路板边线长度（单位为in）；

L——电子元器件的长度（单位为in）；

h——电路板厚度（单位为in）；

r——固定在电路板上元器件的相对位置因子；

C——不同电子元器件类型的常量，0.75<C<2.25。

假定电路板包含一个标准双排封装设备，并焊接在图5-53所示位置中。设置B=3.36in，如图5-54所示。

图5-53 芯片位置

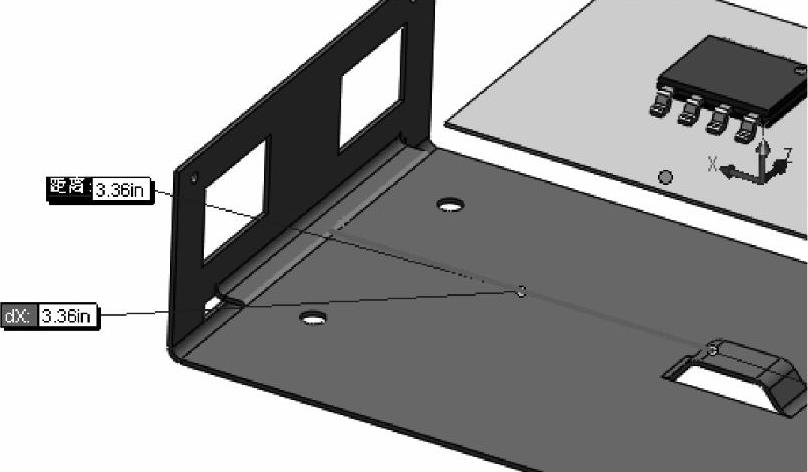
图5-54 尺寸参数

注意，经验公式中的距离等于支撑之间的距离，而不是整个电路板沿Y边线的长度，如图5-55所示。

设置L=0.96in，h=0.03in，r=1（元器件大致位于支撑之间的中间位置），C=1，将这些数值代入上面的公式中可以得到

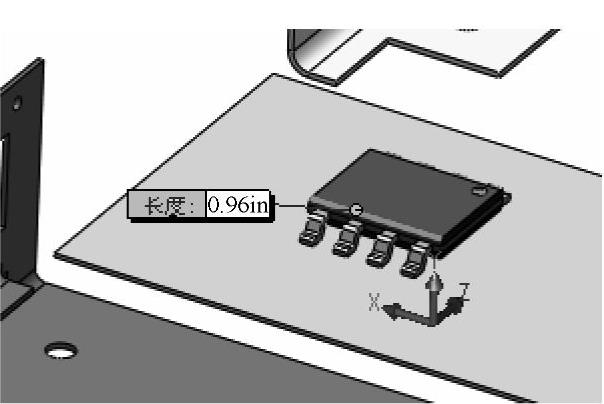
图5-55 边线长度

仿真中的最大3σ位移为3×1.8e-1=0.54mm×1in/25.4mm=0.021in。根据这个经验方法，这个电子元器件将通过2000万个周期的重复考验。

结论 如果所有振动都发生在幅度为0.025in的水平（在随机算法中接近1.17σ），在4.06Hz处的反向应力的主要频率作用下，电子元器件的寿命至少为58天。