电子设备外壳随机振动分析练习

在本练习中，将对一个电子设备外壳进行一次随机振动分析，如图5-35所示。本练习将巩固以下技能：

● 随机振动分析。

● RMS结果。

● 随机算例属性。

项目描述 本章分析了固定在轮船甲板上货柜中的电子设备外壳受到随机振动，参照MIL-STD_-810G中方法514.5的测试标准进行性能鉴定试验。由于外壳是封装在货柜中的，将通过本章计算所得的加速度PSD进行加载，得到输出量的RMS和PSD值，如图5-36所示。

图5-35 电子设备外壳

图5-36 货柜

操作步骤

步骤1 打开装配体文件

从文件夹Lesson05\Exercises\Electronics Enclosure下打开装配体文件“Electronic_As-sembly”。

算例“Random Vibration”已经提前定义完毕，它包含的所有模型特征（材料、夹具和接触）与之前在第2章中使用的完全相同。

步骤2 指定加速度PSD输入

在全局-X方向定义【统一基准激发】PSD加速度，如图5-37所示。

在文件夹Exercises下可以找到文件“acceleration PSD.csv”，曲线数据便来自其中。确认【单位】被指定为（m/s^2）^2/Hz，如图5-38所示。

注意，这里输入的PSD加速度不同于第5章中指定的数值。

图5-37 指定加速度PSD

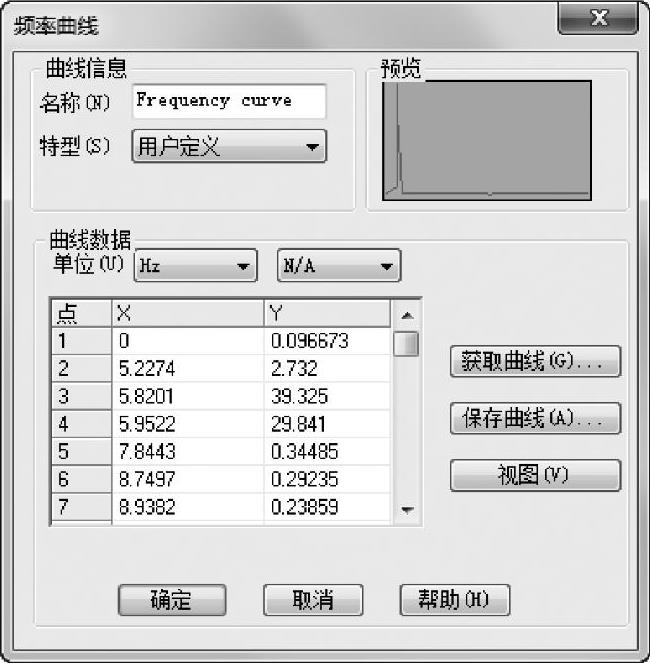
图5-38 编辑曲线

提示

基准激发的PSD加速度一定要在同一方向进行指定，该方向对应于第5章中货柜分析的输入层。由于功能验证测试需要沿着所有三个正交的方向进行仿真，因此有必要分析三次。用户也可以选择在货柜分析中直接包含电子设备外壳箱体，但这将增加网格和问题规模的复杂性，会产生一定的问题。

步骤3 划分网格

以默认单元的【整体大小】4.42mm生成【草稿品质网格】，选择使用【标准网格】。

步骤4 频率分析

针对65个模式运行此频率分析。

提示

在第2章已经得出过结论，即65个模式足够用于该外壳的动态分析。

步骤5 查看模式及自然频率

列举模式如图5-39和图5-40所示。最低和最高频率分别约为49.8Hz和1556.4Hz，如图5-41和图5-42所示。

图5-39 列举模式（一）

图5-40 列举模式（二）

图5-41 最低频率

图5-42 最高频率

步骤6 随机算例属性

设置【上限】为100Hz，【频率点数】为2，如图5-43所示。设置【偏置参数】为2，如图5-44所示。

步骤7 结果选项

设置【保存结果】选项为【对于所有解算步骤】。

提示(www.xing528.com)

当指定【对于所有解算步骤】时，不会显示【图表的位置】选项组，所有节点结果都已经存储好了。

图5-43 算例属性

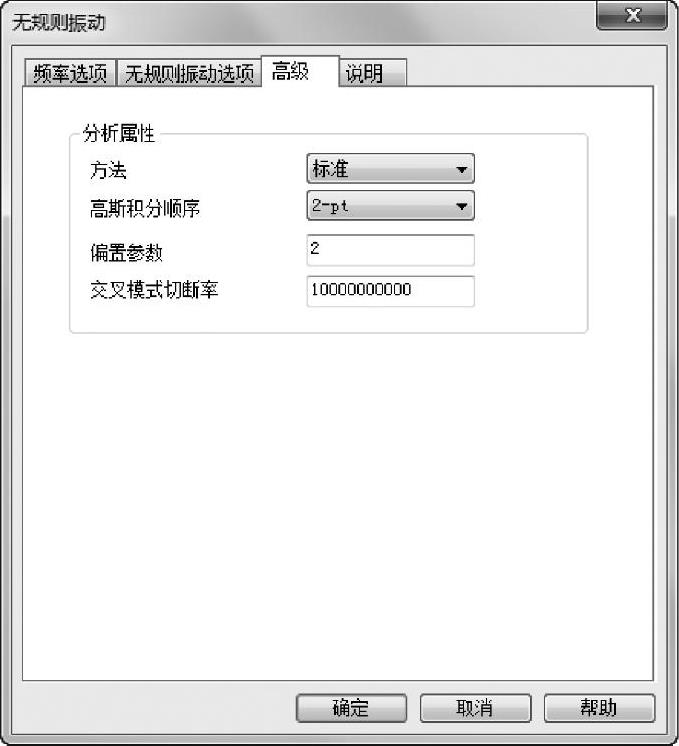
图5-44 设置高级选项

步骤8 阻尼

对于所有65个模式而言，指定【模态比率】为0.05。

步骤9 运行随机振动算例

步骤10 RMS结果

因为输入的PSD加速度在X方向激发外壳，因此所需的结果数值也对应该方向。然而，用户应该经常检查其他方向或合成结果，因为在其他方向也可能存在明显振动。

图解显示X方向的位移、速度和加速度RMS结果，如图5-45所示。

上面的图解分别显示了位移、速度和加速度的最大RMS（或1σ）值为6.27e-4mm、9.3e-2mm/s和0.04g（388mm/s^2）。

图5-45 RMS图解结果（一）

注意

通过观察发现，这些结果可能并不正确。

随机振动结果的准确性 为了计算准确的RMS值并正确地完成运算，需要一个最小数量的计算点。在第4章中，在每两个相邻的自然频率点之间选择了5个点，此外，加载的频率范围（1～100Hz）包含了大量自然频率点（频率范围1～100Hz内总的频率数量点为270），足够用于准确的数值积分和其他计算。

在当前这个例子中，只在每两个相邻频率点之间选择2个点。在1～100Hz这个范围内只包含有一个自然频率，点数总和为5，显然这是不够的。

为了准确求解本分析，需要至少20（越多越好）个计算数据点，因此需要回到模型中，指定一个更多数量的数据点并比较其结果。

步骤11 设置随机算例属性

将【频率点数】增至20。

步骤12 运行随机振动算例

步骤13 RMS结果

图解显示X方向的位移、速度和加速度的RMS结果，如图5-46所示。

图5-46 RMS图解结果（二）

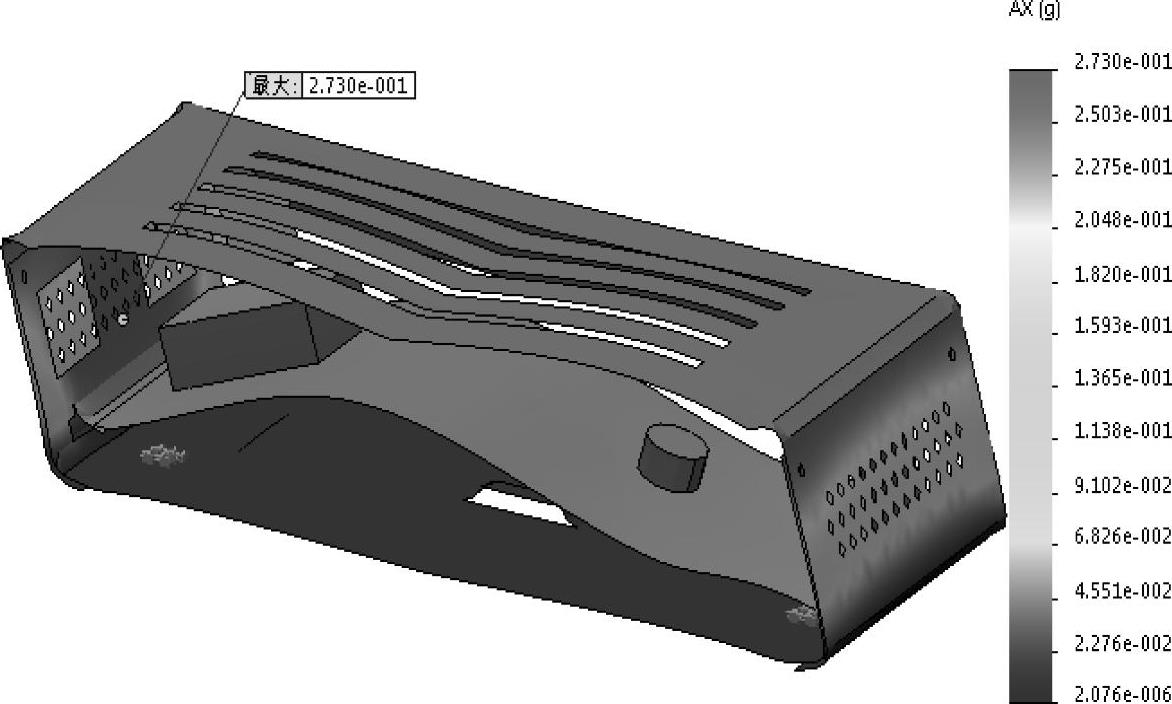
图5-46 RMS图解结果（二）（续）

位移，速度和加速度的RMS（或1σ）最大值分别升至4.3e-3mm（增加583%）、0.3mm/s（增加222%）和0.27g（2676mm/s^2）（增加575%）。

步骤14 vonMises应力的RMS值

图解显示vonMises应力的RMS分布，电子外壳的von Mises应力的RMS（1σ）最大值约为0.43MPa，如图5-47所示。

图5-47 vonMises应力的RMS图解结果

步骤15 响应图表的PSD加速度

在两个定义好的传感器位置，图解显示PSD加速度响应图表的X分量，两条曲线的峰值都位于5.61Hz附近，其大小为3.6e6（mm/s^2）^2/Hz，小于5.61Hz处的其他峰值（17Hz），如图5-48所示。

可以得出结论，外壳将在频率为5.61Hz处发生显著振动：

1σ的加速度幅值为0.27g。有68.4%的时间幅值将小于等于0.27g。

2σ的加速度幅值为2∗0.27=0.54g。有95.4%的时间幅值将小于等于0.54g。

3σ的加速度幅值为3∗0.27=0.81g。有99.6%的时间幅值小于等于0.81g。

对于4σ及更高的结果，或对于应力及其他数值，也可以通过相似方法获得。

图5-48 响应图表