随机振动分析及其载荷特征分析

随机振动分析求解动力学问题，其关联的载荷很难（或不可能）使用普通的数学方程式来描述，这样的载荷被称为不确定的，图5-17所示为载荷时间关系曲线图（载荷历史曲线）的样例。

由于确切地描述载荷时间关系曲线图非常困难或不可能，因此通常使用它的统计特征来进行表示。

下面将一般性地介绍随机载荷时间关系曲线图的假设：

图5-17 载荷历史曲线

1.固定的随机载荷 当统计特征不随时间发生变化时，随机载荷是固定的。这个假设的推论是，任意部分的载荷时间历史，就足够获得整个载荷正确的统计特征。图5-18所示为固定的随机载荷历史曲线。

图5-18 固定的随机载荷历史曲线

固定载荷的假设并没有带来太大的困难，因为从工程的角度来讲，一个随机载荷历史的任意部分都可以假定为固定的。例如，飞机的起飞、巡航和降落代表了飞行过程中三个不同的载荷历史，但在很长的一个时间段内，每一个环节都可以分别视为固定的。

2.随机载荷时间关系曲线图满足高斯概率分布 图5-19给出了一个典型的高斯概率分布的贝尔曲线的例子。

在随机振动理论中使用的基本统计特征如下：(www.xing528.com)

• 平均值：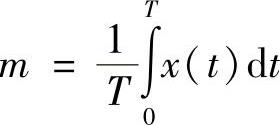

• 方均根值：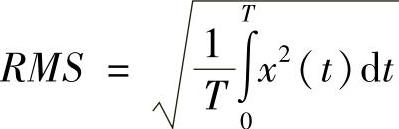

• 方差：σ²=RMS²-m2

图5-19 随机载荷历史曲线

• 标准差：σ

之前的载荷时间关系曲线图得到的平均值是一个常数，可以使用传统的静态应力分析方法进行处理，因此在随机振动分析中没有必要，需要将其从随机载荷历史中去掉。可以得到一个重要的结论，当设置m=0时，方差和标准差之间的关系式为

σ=RMS

RMS是从随机振动分析中获取的两个主要结果量之一。从上面的公式可知，它代表最终幅值（位移、速度、加速度或应力）的一个标准方差（1σ）。