支架的谐波分析

本章，将对一个支架完成一次谐波分析。

操作步骤

步骤1 打开装配体文件

打开文件夹Lesson03\Case Study下的文件“Bracket Assm”。

步骤2 生成谐波算例

生成一个【线性动力】算例。在【选项】下方，选择【谐波】，将此算例命名为“Harmonic Analysis”，如图3-4所示。单击【确定】。

步骤3 指定材料

对零件“Box”指定【AISI1020钢】，对“bracket”指定【PE高密度】。

步骤4 定义远程质量

“Box”将在远程质量特征的协助下进行模拟。在零件文件夹下右键单击“Box”，选择【视为远程质量】，选择bracket的两个柱形圆孔，作为【远程质量的面、边线或顶点】，如图3-5所示。单击【确定】。

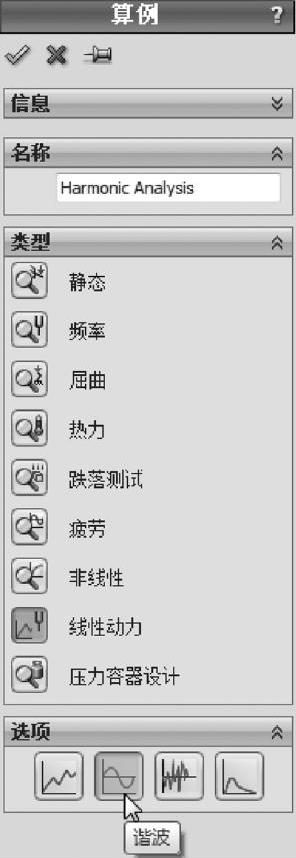
图3-4 定义谐波算例

步骤5 应用约束

右键单击【夹具】文件夹，选择【固定铰链】，选择四个柱形圆孔（其轴沿全局Y向），如图3-6所示。单击【确定】。

步骤6 应用载荷

如图3-7所示添加【力】，选择两个柱形圆孔（其轴沿Z向）。在【方向】中选择Top Plane，在【垂直于基准面】方向输入1N，确保力的方向与图中一致。

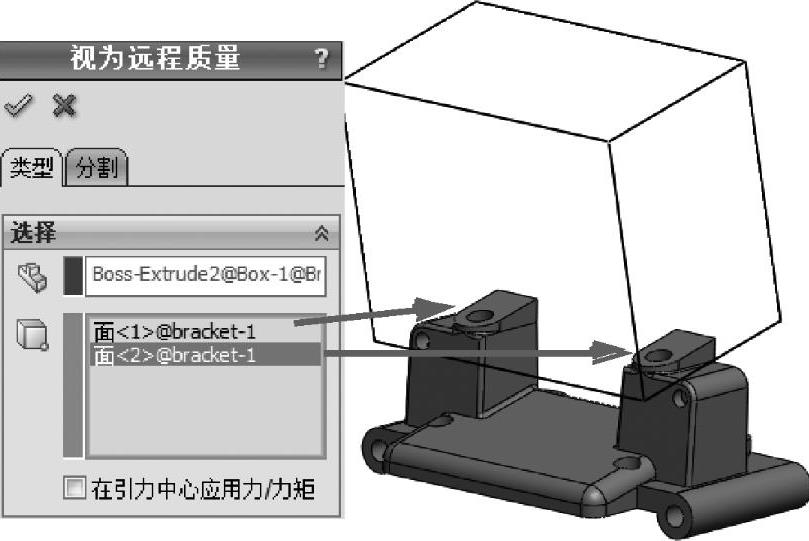
图3-5 定义远程质量

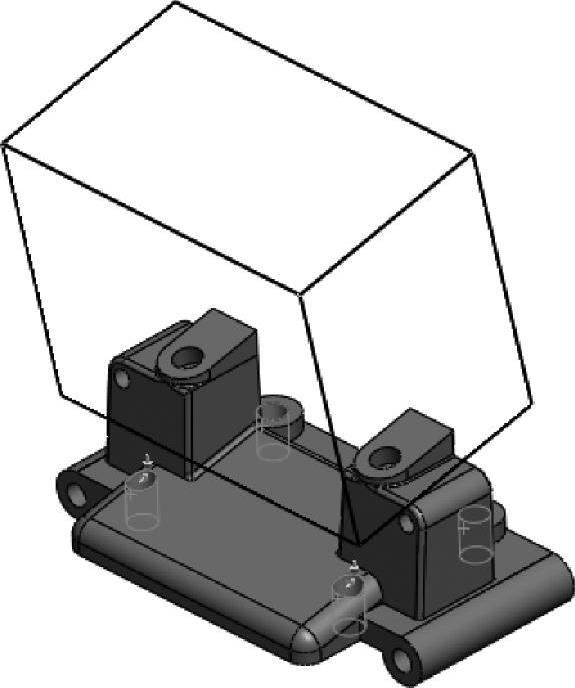
图3-6 应用约束

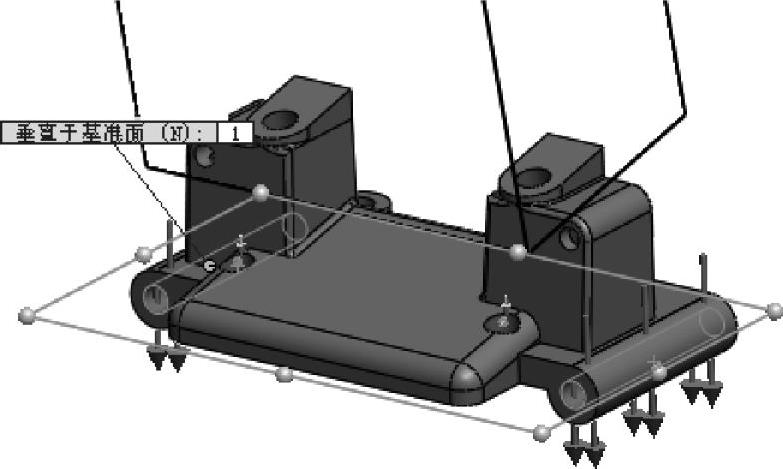
图3-7 应用载荷

在【带频率的变量】选项组中，选择【曲线】并单击【编辑】按钮，如图3-8所示。更改【单位】为Hz，输入数值，如图3-9所示。

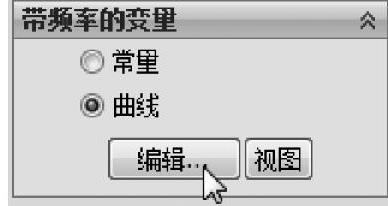
图3-8 编辑曲线

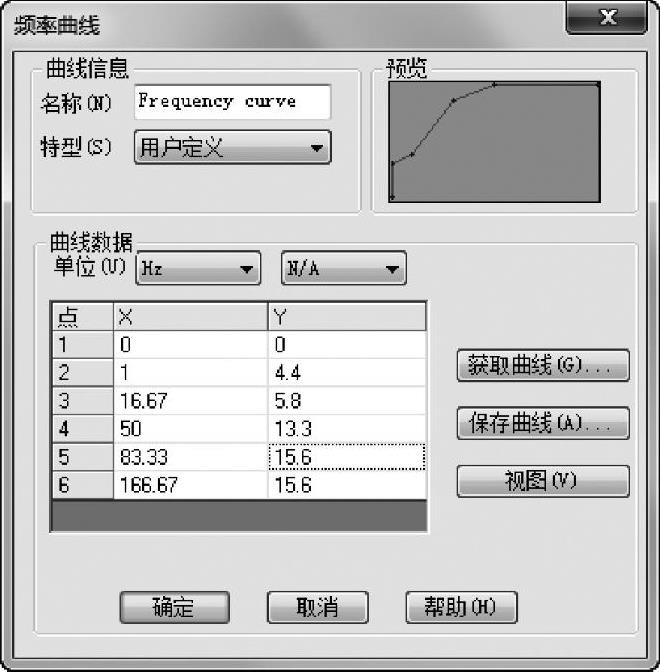
图3-9 定义曲线

在【频率曲线】对话框和【力/转矩】的PropertyManager中分别单击【确定】。

提示

输入的转速必须转换为Hz或rad/s作为单位。为了得到以Hz为单位的输入数值，需将给定的转速值除以60。

步骤7 划分网格

生成【草稿品质】的【基于曲率的网格】，将【最大单元大小】和【最小单元大小】分别指定为1.5mm和0.5mm，【圆中最小单元数】为8，【单元大小增长比率】为1.5，结果如图3-10所示。

提示

远程质量无需划分网格。

步骤8 指定算例属性

右键单击谐波算例并选择【属性】，在【频率选项】选项卡中，【频率数】保持默认数值15，解算器指定【Direct sparse】，如图3-11所示。

图3-10 划分网格

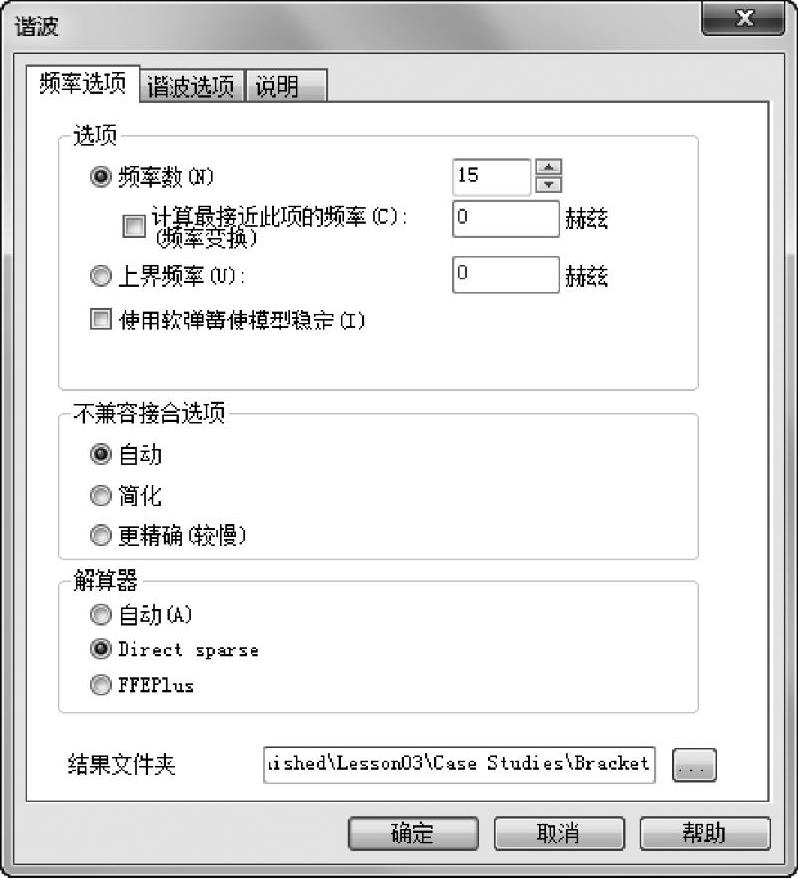
图3-11 指定算例属性

提示

当使用远程质量时，由于FFEPlus解算器可能遇到收敛问题，因此推荐使用Direct sparse解算器。

步骤9 指定谐波选项

单击【谐波选项】选项卡，在【工作频率限制】中设置【单位】为【周期/秒（Hz）】，【下限】为0，【上限】为166，如图3-12所示。

步骤10 指定高级选项

单击【高级】选项卡，在【每个频率的点数】中输入15，在【每个频率的频宽】中输入0.4，保持默认的【插值】为【对数】，如图3-13所示，单击【确定】。

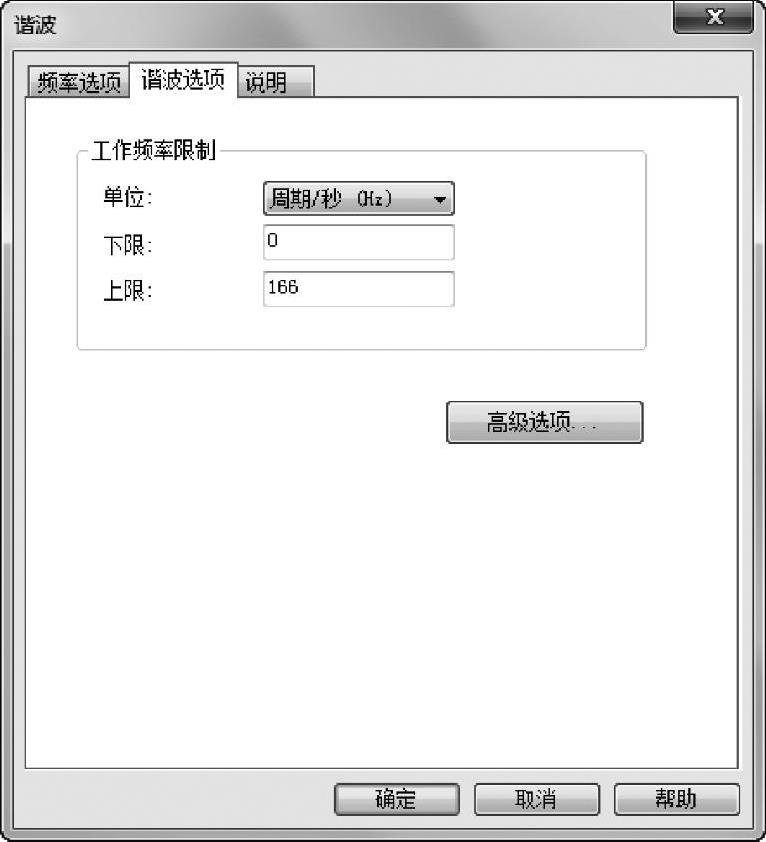
图3-12 指定谐波选项

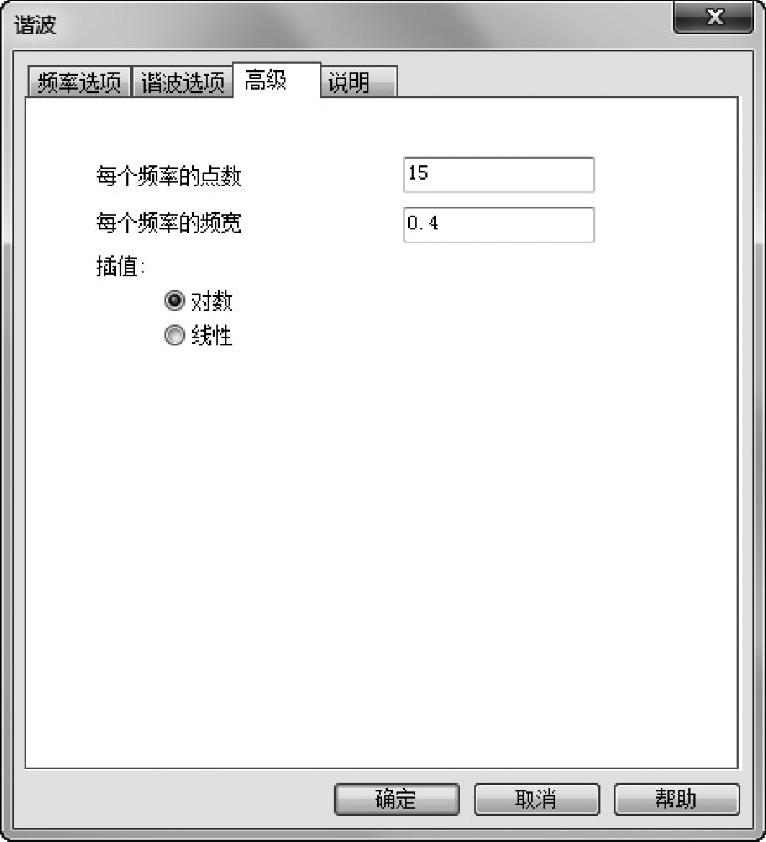
图3-13 指定高级选项

谐波算例将求解所有包含在要求的频率范围（本例中为0～166Hz）内的自然频率点，为了正确地扫描整个要求的频率范围，还需要更多的频率点，额外频率点的数量和分布通过高级选项中的参数进行辅助控制。

【每个频率的点数】：每个频率都由指定数量的额外点围绕。

【每个频率的频宽】：在额外点分布的地方，这个参数用于控制围绕每个频率的频宽。

【插值】：控制额外频率点的间隔。

关于这些参数的更多信息，请参考SOLIDWORKS Simulation的帮助文档。

步骤11 运行频率

步骤12 列举共振频率(www.xing528.com)

通过观察发现有两个频率（56.02Hz和158.71Hz）落在要求的工作频率范围（0～166Hz）内，如图3-14所示。

步骤13 列举质量参与因子

【质量参与因子】的总和值远高于推荐的数值0.8，如图3-15所示。

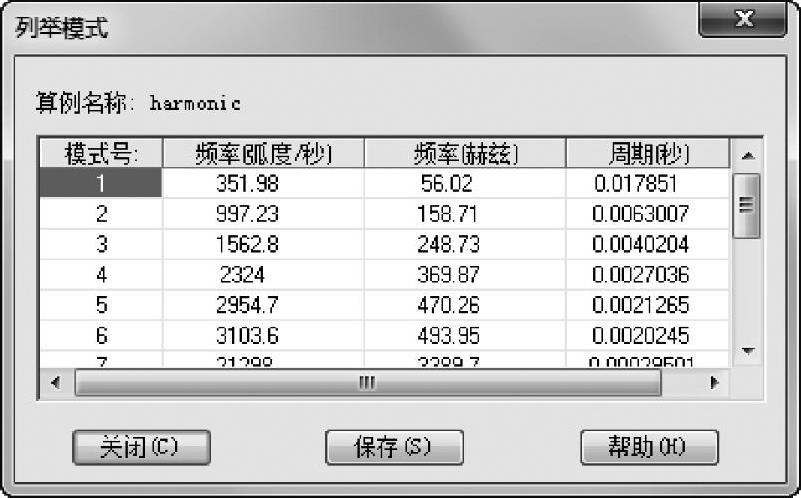
图3-14 列举模式

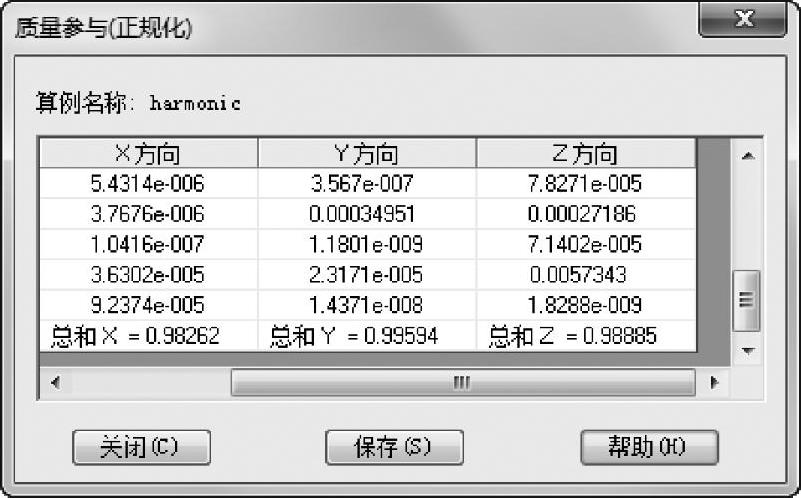
图3-15 质量参与因子

步骤14 图解显示更高的模式形

图解显示更高的（第15个）模式形状，结果如图3-16所示。最高的模式对应的离散是正确的。

图3-16 网格分布

步骤15 指定阻尼

定义【模态阻尼】，对所有5个模式指定【阻尼比率】为0.03。

步骤16 结果选项

在【结果选项】中，保留默认设置，所有频率计算点将保留所有模式下完整的结果。

提示

如果问题规模变大，或频率点数增加，对存储空间的需求可能也会急剧上升。

步骤17 运行算例

步骤18 位移结果

对最后一个频率步骤图解显示合位移。在【零部件】中选择【URES：合位移】，在【单位】中选择m，如图3-17所示。确保【图解步长】显示的为分析中计算的最后一个步骤，结果如图3-18所示。注意到工作频率最大位移的上限非常小。

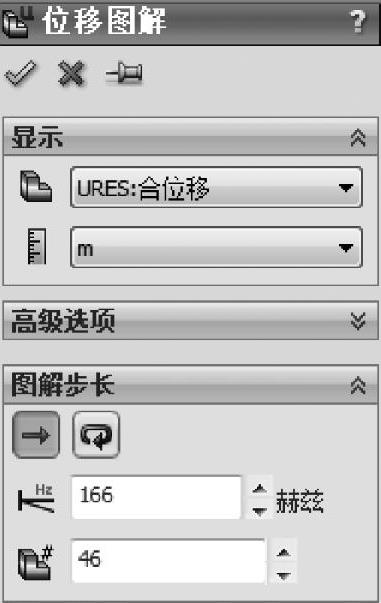
图3-17 定义位移图解

图3-18 位移图解（一）

步骤19 探测位移

在图3-19所示的拐角顶点探测位移，这个位移非常接近附着零部件的位移。

步骤20 图解显示响应图表

在【报告选项】中单击【响应】按钮。图3-20所示的【响应图表】显示了在工作频率下这个位置各种数值的位移大小，注意到最大位移发生在第一个共振频率56.08Hz处，在第二个共振频率158.68Hz处没有很大的位移。

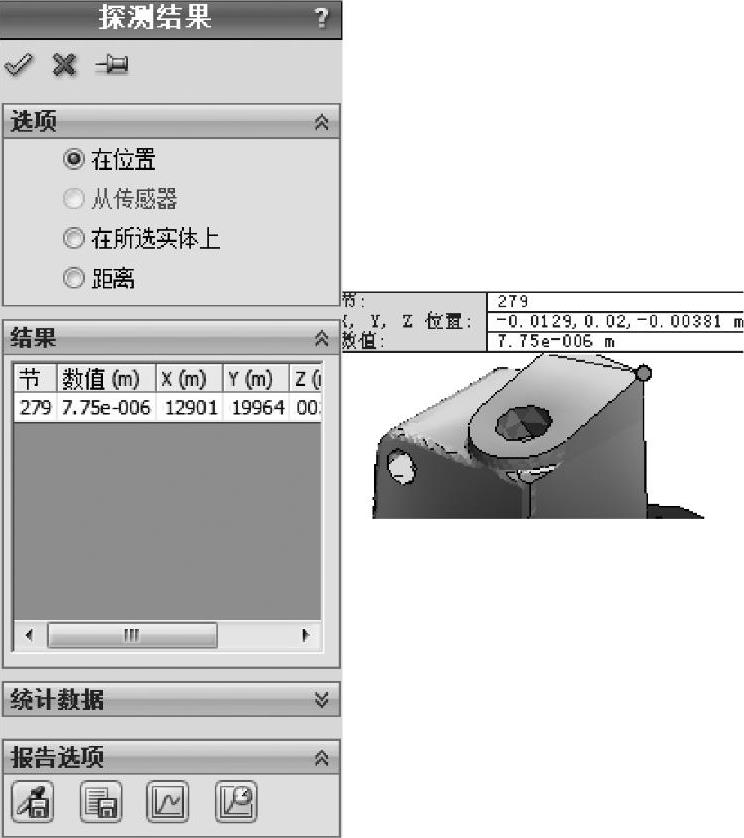
图3-19 探测位移

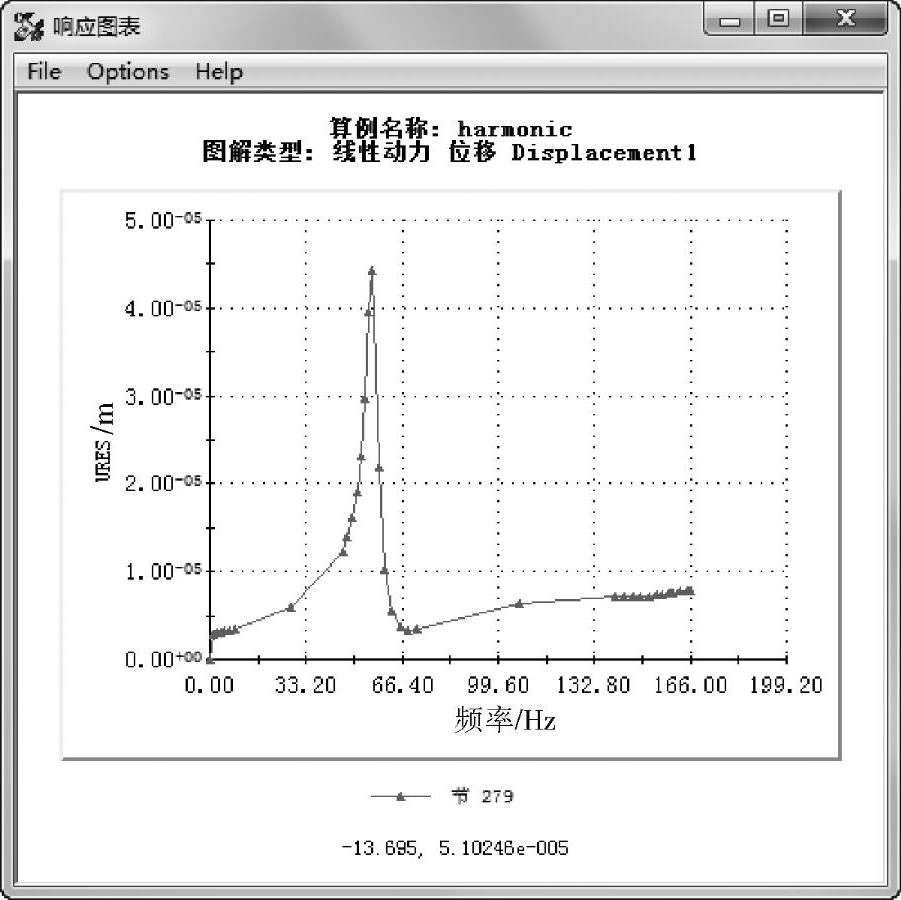
图3-20 响应图表

步骤21 位移结果

当工作频率与第一个自然频率一致时，图解显示其合位移，如图3-21所示。

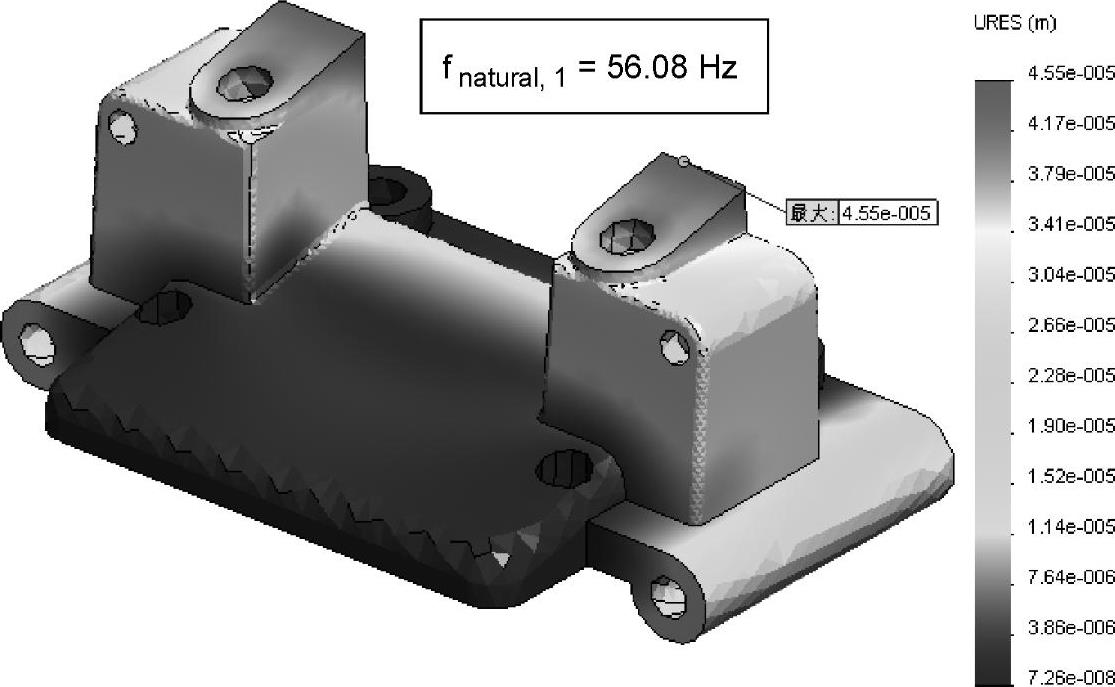
图3-21 位移图解（二）

当工作频率为56.08Hz时，最大位移的大小为4.55×10^-5m。查看位移大小的一个好方法是对所有频率步长使用一个封装图解。

步骤22 所有频率位移图解的边界

编辑任何一个位移图解，单击【图解步长】下的【穿越所有步长的图解边界】按钮，如图3-22所示。

穿越所有频率步长的最大合位移大小，真实发生在工作频率与第一个自然频率56.08Hz重合时。

步骤23 应力结果

对【von Mises应力】，要求显示【穿越所有步长的图解边界】的图解。设定【变形形状】为【真实比例】，如图3-23所示。

图3-22 穿越所有步长的位移图解

图3-23 穿越所有步长的vonMises应力图解

在给定工作频率的范围内，模型中的最大应力为3MPa。虽然这个数值低于抗拉强度22.1MPa，但接近强度极限并不安全。用户可能希望将应力限制到一个更小的数值，同时，因为应力最大值发生在支撑位置，可能需要采用更好的建模方法，以获取更加真实的应力结果。

总结 本章使用谐波分析计算了简谐力作用下车灯支撑用支架的响应大小。在每个工作频率下，

作用力都显示了不同的大小（本章开始的表格中显示了相关内容），最大的结构响应发生在力作用下的

工作频率与支架的其中一个自然频率重合时。为了模拟附着零部件的效果，使用了远程质量。临界响

应幅度发生在第一个自然频率56.08Hz处。

提问

● 谐波分析（会/不会）假定以振荡的方式加载振荡。载荷振幅（可能/不可能）随时间衰减

● 谐波分析的输入（是/不是）载荷变动与时间的函数。

● 谐波分析的输出（是/不是）最终振幅变动量与时间的函数。

● 在谐波分析中载荷（是/不是）表示为在变化的加载频率下的振幅，输出也（是/不是）只表示在相同频率下最终的振幅大小。