时间步长参数对波动方程模拟的影响

最小时间步长非常重要，而且需要考虑大量参数。太大的时间步长可能导致分析无法完成，或者尽管在过大的一个时间步长下能够完成分析，其结果也可能是错误的。在确定最小所需的分析时间步长时必须考虑以下参数：

1.最高且重要的模态波的时间分辨率 在这个分析中，最后一个重要的自然模式对应的振动应该至少离散为5（最好为10）个时间增量。也许对于一个没有经验的用户而言，比较难确定什么是最高且重要的模式，因此这里必须考虑最高的模式。必须随时考虑这个准则

Δt<0.1T_min=0.1×0.00064251s=6.4×10^-5s

2.弹性应力波传播的分辨率 如果模型中需要用到弹性应力波传播的分辨率，必须根据下面的公式计算时间步长

上面公式中用到的弹性模量及质量密度来自外壳的材料（铝合金1060-H18），单位系统为米制SI，外壳的长度大约为192mm。注意，参数0.2在5个时间步长中离散弹性波，如果需要更好的分辨率，则可以调节这个参数。

3.载荷的时间分辨率 这对准确求解冲击载荷是至关重要的。如果分辨率过低，某些波的特征可能会被忽略，从而导致载荷描述可能变得非常不准。在分析中，冲击脉冲将采用10个时间点进行离散。因此

Δt<0.1（pulseduration）=0.1×0.011=1.1×10^-3s

经典冲击载荷的频率特性非常容易确定，然而确定一般振动冲击载荷的频率特性则要困难得多。载荷的傅里叶变换可以显示载荷的频率特性，图2-24显示了本章中使用的经典冲击脉冲的傅里叶变换，可以观察到峰值振幅发生在46.8Hz处，对本例而言并没有太大的困难。最高模态波的频率（发生在1556.4Hz处，或时间周期为0.00064251s处）相当高，在时间步长为6.4×10^-5s时能够准确求解。一般而言，最大幅度的极值，以及载荷振幅谱的重要部分都应该被离散。

图2-24 经典冲击脉冲

注意

分析中包含的最高模态波的频率必须高于载荷所有重要的频率，或用户感兴趣的重要频率。

在分析中，选择时间步长Δt=5×10^-5。除了应力波传播以外，所有时间增量的标准都满足要求，只有应力传播非常重要时，这个标准才必须满足要求。如果对位移、速度和加速度要求更高，就可以不强求应力传播这个标准。

步骤29 定义高级选项

在【模态时间历史】对话框中，单击【高级】选项卡，如图2-25所示。

图2-25 定义高级选项

在【时间积分法】中，保留默认的选项【纽马克（新标记）法】，第一积分参数和第二积分参数的数值也保留默认值。

提示

对时间积分法的描述，请参见本书第6章。数字参数用于调节时间积分过程中时间域加速度的近似值。默认值适用于大多数应用，一般而言不需要进行修改。进阶学员可以自行查阅大量关于此主题的已有文献，以获取更多信息。

步骤30 定义传感器

在SOLIDWORKS特征树中，对图2-26所示的两个位置定义【Simulation数据】和【工作流程灵敏】传感器。

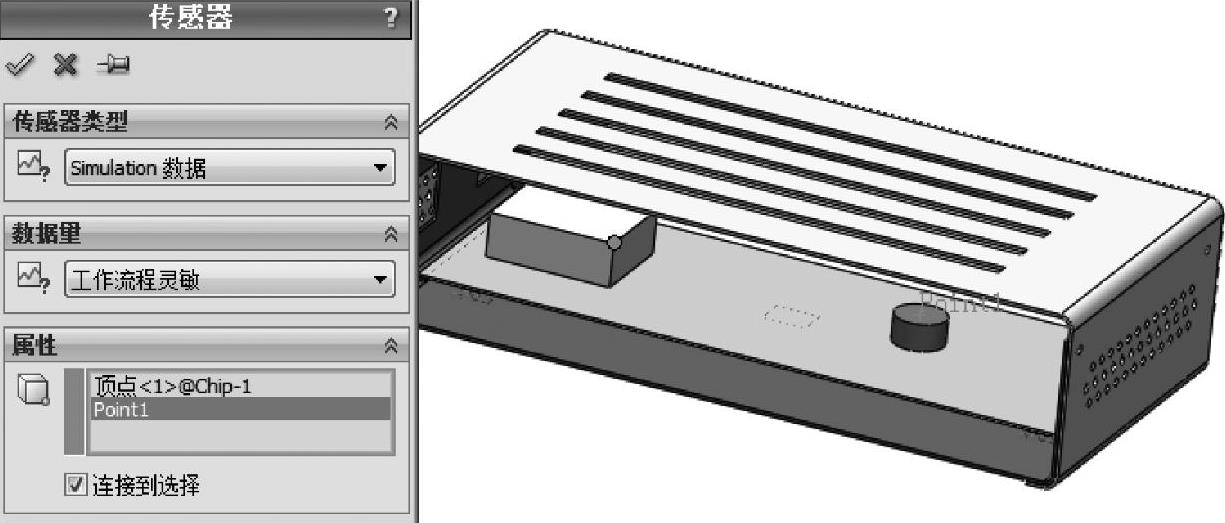
图2-26 定义传感器

这些位置代表重要的组件及区域，动态分析结束后将图解显示具体的图表。下面的步骤将指定存储需求。

步骤31 结果选项

动态分析可能产生巨大的数据量，推荐在运行分析之前指定所选的数据。

在【结果选项】下，选择【保存结果】下的【对于所指定的解算步骤】。【数量】选项组，选择【位移和速度（相对）】并勾选【应力和反作用力】复选框。

对全部结果指定三组保存为轮廓图解，注意到每组都设置了一个不同的增量，以降低存储需求。

仍然在【结果选项】下，【图表的位置】选择【Workflow Sensitive1】作为传感器清单。对所有时间步长，都将保存传感器位置的完整数据，如图2-27所示。单击【确定】。

提示

相对位移将参照移动的“base”，绝对值也将包含“base”的位移，通常使用的是相对值。

步骤32 保存并运行

【保存】分析的设置，【运行】该动态分析。

步骤33 图解显示位移结果

图解显示【UX∶X位移】分布，如图2-28所示。(www.xing528.com)

在【图解步长】选项组中，单击【单步长的图解】按钮并指定【图解步长】为10（这个图解步长对应的时间为0.00905s）。

在【变形形状】选项组中，确认选择了【自动】，如图2_-29所示。

在【自动】变形形状的数值下，图解显示在夸大的变形中，这是由于零件显示为严重贯穿的原因，然而，这只是一个视觉表现，模型中不存在这样的穿透关系。用户可以将此数值更改为【真实比例】（或1∶1），以观察结构变形的真实大小，真实的位移其实非常小。

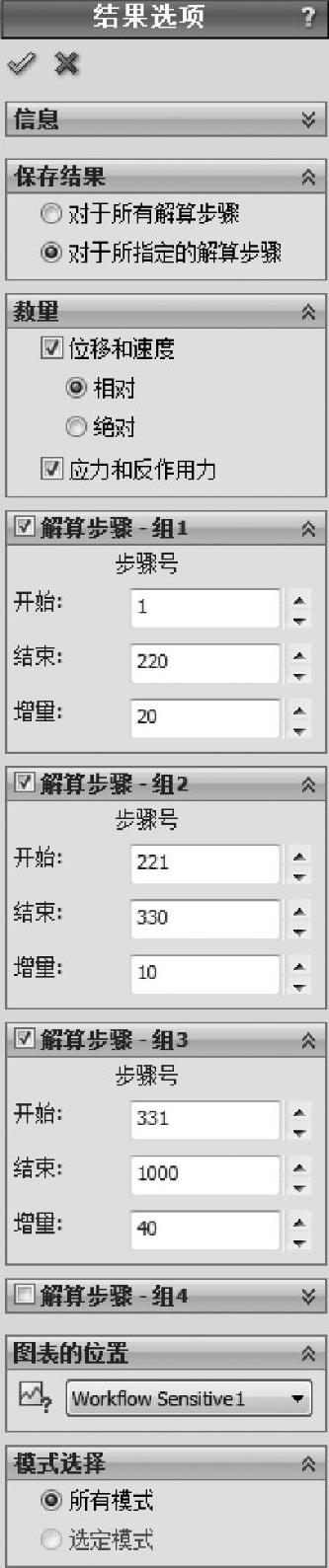
图2-27 定义结果选项

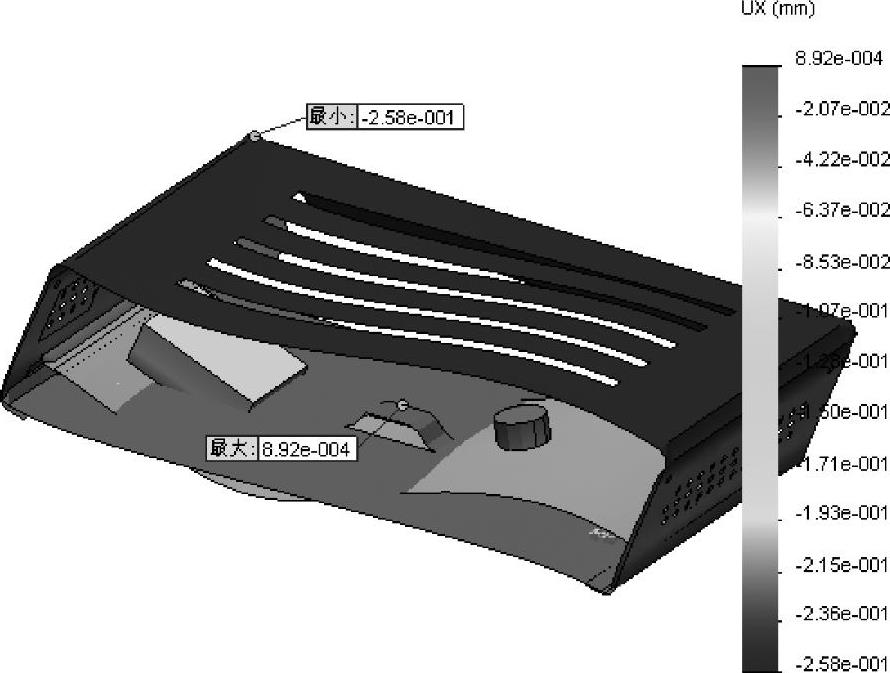
图2-28 图解显示位移结果

事实上，确实存在一定的穿透，但可以忽略。可以看到，在第10个步长的最大位移为-0.26mm。【动画】显示变形，以验证结果是符合预期的。

步骤34 编辑图解

在【图解步长】下（图2-30），单击【穿越所有步长的图解边界】按钮并选择【最大】，结果如图2-31所示。

图2-29 定义位移图解

图2-30 修改选项

图2-31 穿越所有步长的最大位移图解

生成一个类似的穿越所有步长的图解边界的图解，这次选择【最小】，结果如图2-32所示。

从图2-31、图2-32中观察到，沿全局X轴的最大和最小位移分别为2.68e-1mm和-3.29e-1mm。这些数值需要和所需数值进行比较，以判断外壳是失效还是合格。

图2-32 穿越所有步长的最小位移图解

提示

大多数情况，更关注加速度（或速度）的结果，而不是位移。

步骤35 加速度结果

设置单位为g，生成【最大】和【最小】的两个【ARES：合加速度】图解，并指定【穿越所有步长的图解边界】，结果如图2-33和图2-34所示。

图2-33 穿越所有步长的最大合加速度图解

图2-34 穿越所有步长的最小合加速度图解

可以观察到，总体的最大合加速度为37.2g。再次对比许可的范围，以判断外壳运转良好还是失效。然而，对电子产品的设计而言，最重要的结果是PCB组件的加速度。

步骤36 在传感器位置的响应图表

设置单位为g，对保存的传感器位置生成【加速度】，【ARES：合加速度】的响应图表，如图2-35所示。

对两个监测的位置而言，总体最大合加速度几乎相等，即最大激发加速度为20g。同时，由于峰值振幅通常发生在初始冲击作用之后的时间，推荐在更长的持续时间内运行分析，直到振动衰减到比较低的水平。

通过细化网格和增加经过考虑的模式数量，来验证瞬态分析结果的正确性是一个很好的习惯。从这样细化后的分析中得到的结果和初始分析的结果应该相差不会太大。如果相差很大的话，说明初始分析的结果不正确，而必须考虑更多的模式和更细的网格。如果分析中忽略了某些重要的结构模式，这种情况就有可能发生。

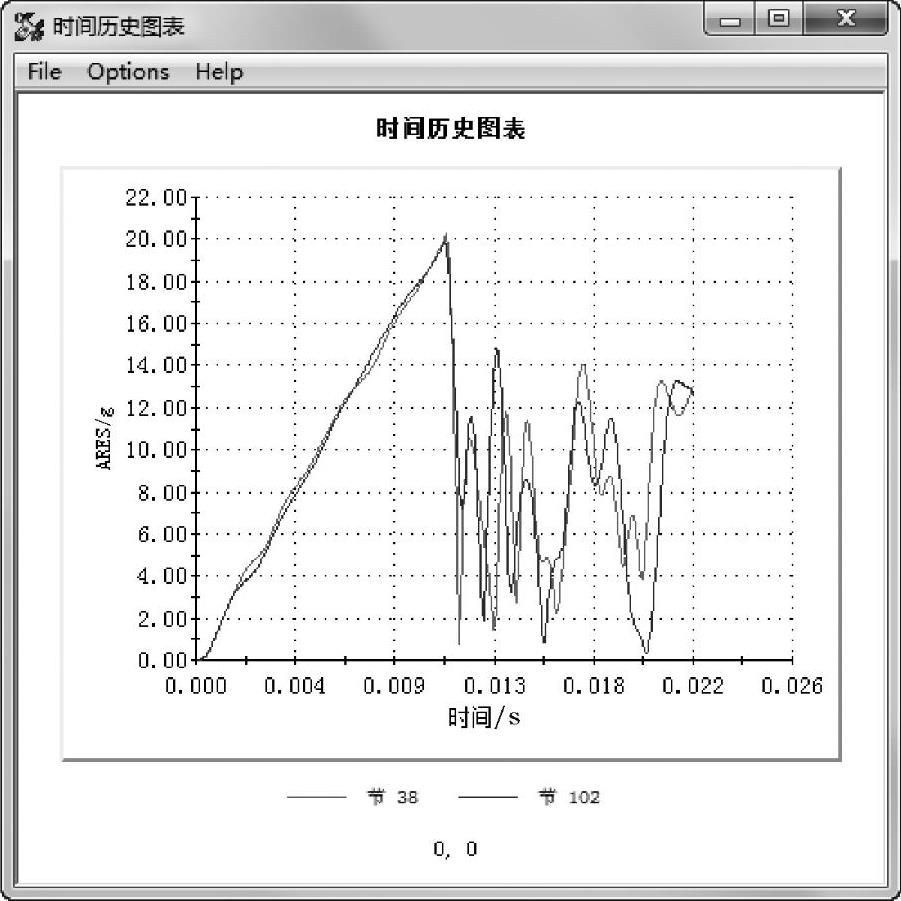
图2-35 响应图表