如何测量粘性阻尼常数？

1.单自由度的粘性阻尼 如图2-20所示，质量为m，刚度为k，阻尼为c的单自由度结构粘性阻尼中，通常以下面的常数为特征阻尼常数为c，阻尼比率为ζ，其中。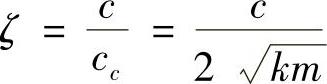

图2-20 力学模式

瑞利阻尼为

c=α·m+β·k

常数之间的关系为

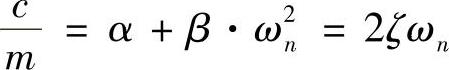
注意到上面的常数表示了一定刚度和质量的结构，它们不代表材料，而只代表结构。为了保持一致，本章的后面部分只要提到阻尼，均指结构阻尼。

2.有限元结构的粘性阻尼 在模态分析中，表示FEA结构的一组复杂的微分方程被分解并简化为一组独立的方程，每个这样的方程都代表一个单自由度的振荡器，它们解的组合等于整个结构的响应。于是，在模态分析中，每个独立的模态方程都可以独立地衰减（例如，每个模态方程可以拥有不同的模态常数大小），因此，阻尼常数与那些用于单自由度的阻尼常数是一样的阻尼矩阵为[C]，模态阻尼比率矢量为[ζ]，其中。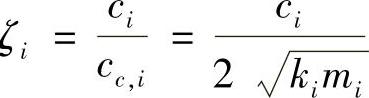

矩阵形式的瑞利阻尼

[C]=α·[M]+β·[K]

以系数形式表述为

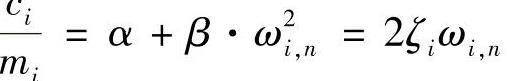
3.结构粘性阻尼的其他数值 文献中经常使用下面的结构阻尼的数值，它们全部与阻尼数值相关。系统损耗系数为η=2ζ

系统的特定吸振能力为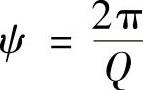

系统自由振动的对数衰减为δ=2πζ

谐振放大（或特性）系数为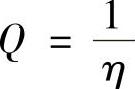

注意：上面的关系适用于展现小振幅的结构。

另外一些比较少见的数值为混响时间、相位角、平面弯曲波衰减以及平面纵波衰减。

4.如何获取阻尼常数 获取相关的阻尼常数是相当困难的，用户通常有两个选择：(www.xing528.com)

1）现有文献。有必要搜索现有的文献，获取相似类型、形状以及材料成分的结构常数，一些文献可能也列出了材料性质的阻尼属性。

2）实验。有可能通过实验的方法测量某些阻尼常数。例如，通常利用实验的方法来表现振动衰减的大小。

步骤27 基本运动

在【外部载荷】文件夹下，指定【统一基准激发】中的加速度大小为20g。

注意

使用外壳的竖直表面作为参考，确保显示的方向如图2-21所示。

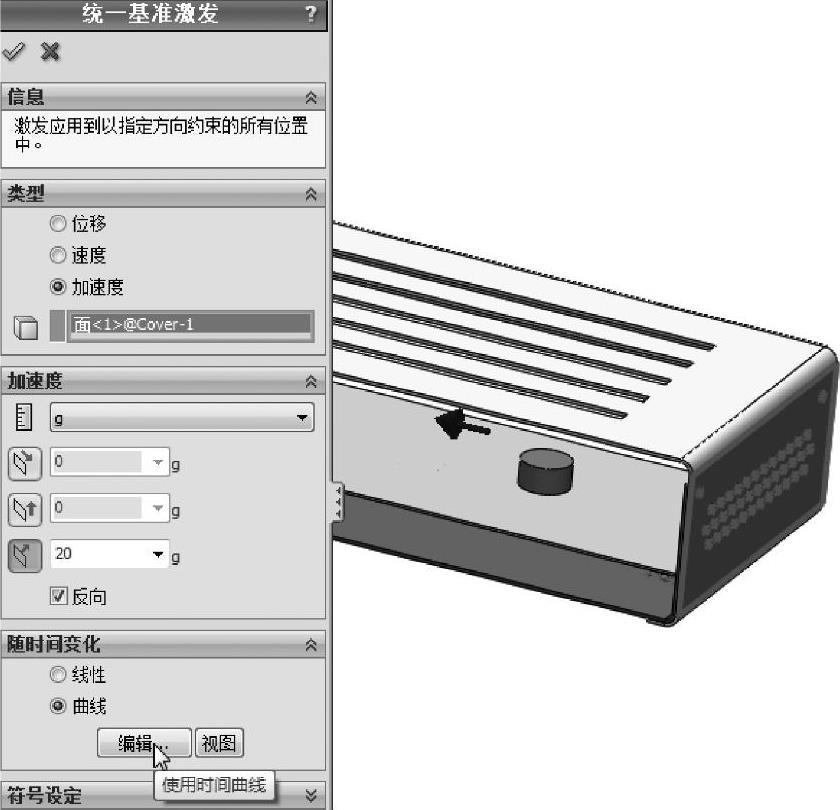
图2-21 定义统一基准激发

在【随时间变化】选项组中，选择【曲线】并单击【编辑】按钮，指定如图2-22所示的数据点，单击【确定】。

提示

上面指定的一个典型冲击并不是标准MILS-STD-810G，方法516.5中推荐的首选为冲击载荷。此处更推荐使用真实的、重复的测量冲击数据，或从之前的冲击响应谱（SRS）估算的合成冲击。只有在没有数据可用时才允许使用经典的冲击脉冲，而且使用时必须与真实的载荷条件对应的脉冲保持一致。

步骤28 时间步长及分析持续的时间

在算例属性的【动态选项】选项卡中，分别指定【时间增量】为5e-5s，【结束时间】为0.022s，如图2-23所示。下面将讨论如何确定时间步长。

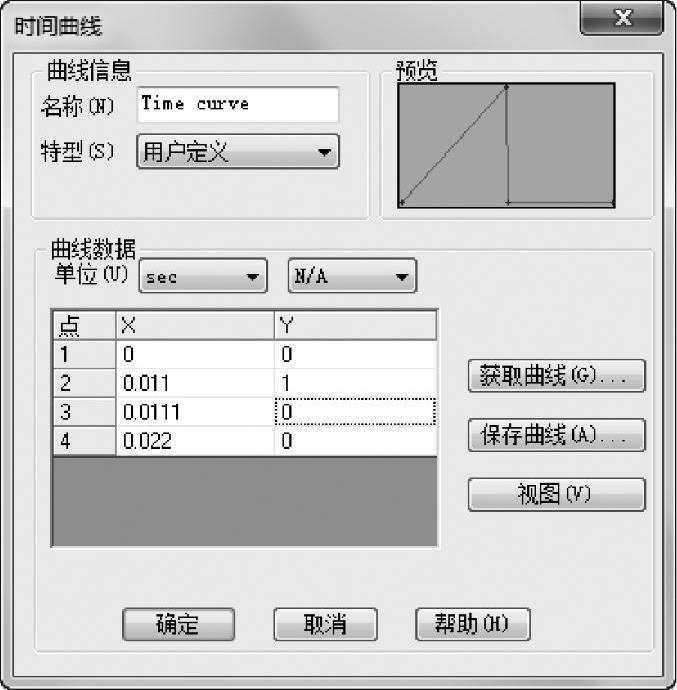
图2-22 定义时间曲线

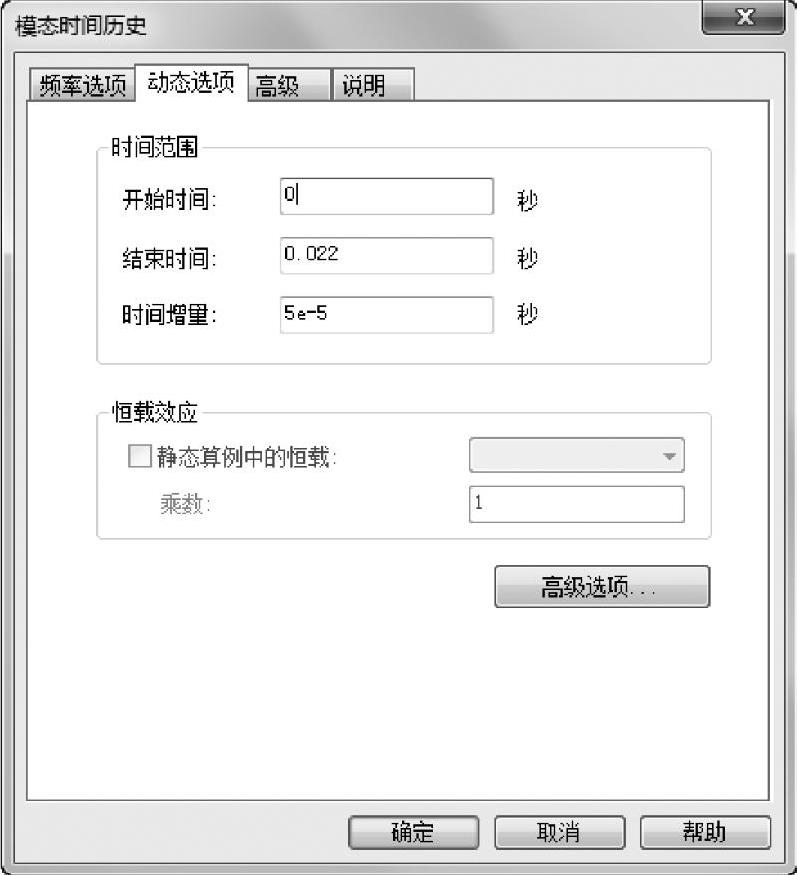
图2-23 定义动态选项

提示|

一般而言，分析持续的时间取决于包含了足够的振动峰值响应。对高频响应而言，分析持续的时间要小于低频响应振动下使用的时间，标准MILS-STD-810G详细说明了如何计算最小的分析持续时间。如果没有测量数据，飞行装置性能测试下冲击响应推荐的近似持续时间为15～23ms，在分析中选择的数值为22ms，是经典冲击脉冲持续时间的两倍。