本章的最后一部分将分析当快速加载作用力时弯管结构的瞬态响应,和之前的动态分析一样,这里不应用阻尼。
步骤21 新建一个线性动力算例
复制算例“Slow force”到一个新的【线性动力】算例,命名为“Fast force”。
步骤22 编辑力
【编辑定义】力的时间曲线,注意到力以更快的速度增大,如图1-20所示。
步骤23 算例属性
确保算例属性设定的值和算例“Slow force”中设定的数值保持一致。也就是说,请确认自然频率数指定为5,时间步长指定为0.0003s。
步骤24 运行算例
同样,本次运算大约需要几分钟时间。
步骤25 位移结果
对最后一个保存的时间步(接近1s)图解显示【URES:合位移】。
最后一个保存的时间步对应的最大合位移为1.59mm,如图1-21所示。和步骤20中显示的一样,整个动态运动中结构的最大位移必须来自所有保存的时间步。
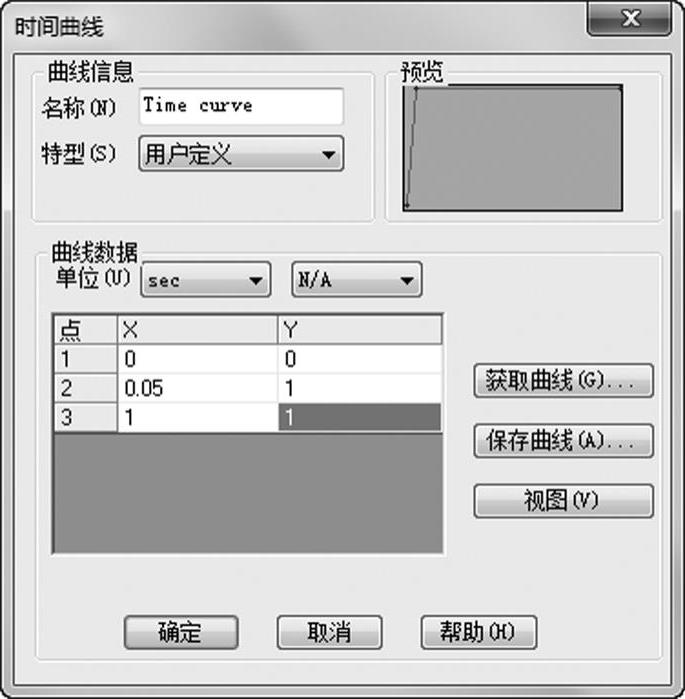
图1-20 定义时间曲线

图1-21 位移结果
步骤26 显示穿越所有时间步的图解(https://www.xing528.com)
【编辑定义】位移图解,并要求图解显示穿越所有步长的图解边界。在所有保存的时间步之中,弯管的最大位移为2.25mm,和最后一个时间步中得到的最大值(1.59mm)明显不同,如图1-22所示。
步骤27 生成末端位移图解
在弯管顶部生成合位移的末端位移图解,如图1-23所示。将上面得到的末端位移图解与算例“Slow force”中得到的顶部末端位移图解进行对比,可以看到振荡幅度明显更高。

图1-22 穿越所有时间步的结果
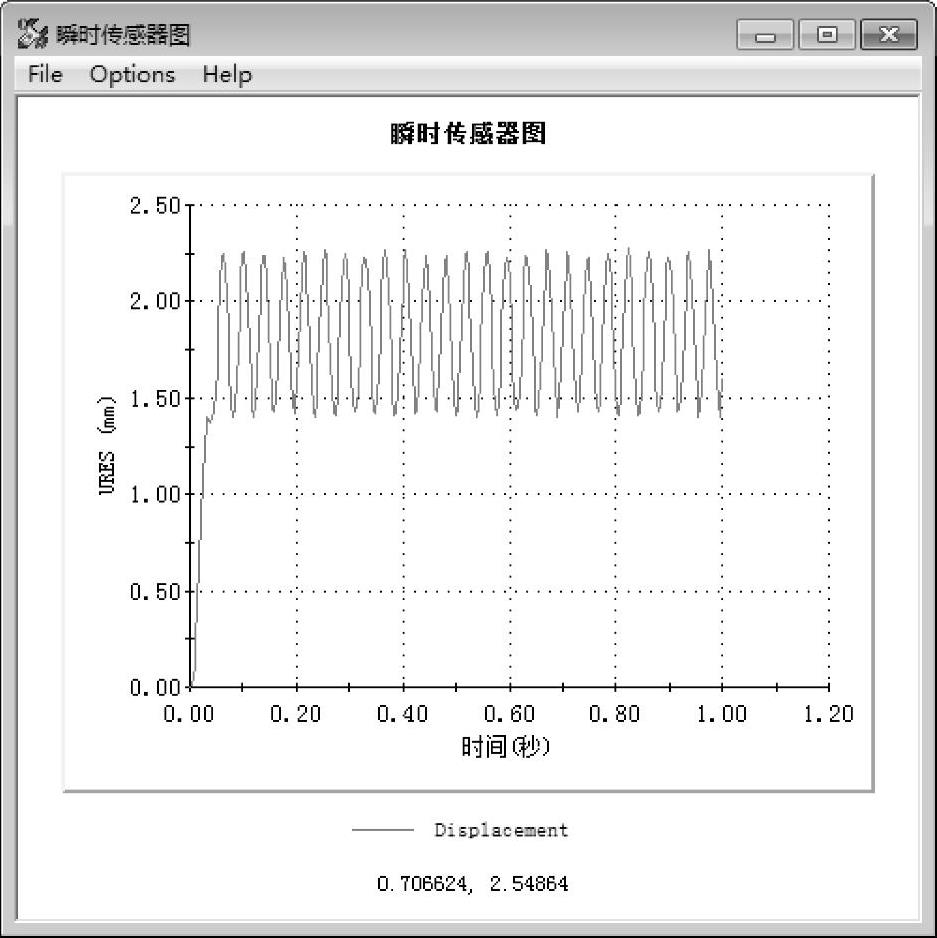
图1-23 末端位移图解
总结 本章展示了一根弯管在集中力载荷下的简单问题,可以看到,缓慢加载作用力的动态分析的结果非常接近静态分析中的结果。这也验证了静态分析中的基本假设,即作用力必须随时间缓慢加载,以减小惯性力的影响。
在算例“Fast force”中,力的大小突然增加,得到的结果也完全不同,这是由惯性效果导致的。
本章还介绍了如何计算最小时间步增量的基本估值。第2章将重点介绍时间步的计算、自然模式的数量以及线性动态分析的其他方面。
本章计算出了弯管的瞬态响应。为了验证结果的正确性,可以细化网格,在方案中纳入更多的自然频率,或减小时间步长。
提问
● 如果只包含一个自然频率,结果会怎么样?
● 在求解线性动态问题时,SOLIDWORKS Simulation使用的求解方法的名称是什么?
● 用户如何在动态分析中计算求解步骤的数量?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




