动态分析：缓慢作用力的影响

本部分将分析在缓慢加载力的作用下弯管结构的瞬态响应。

注意，本章不会在这个动态方法中加载阻尼。阻尼的问题将在第2章讨论。运动的结构矩阵方程式表达如下

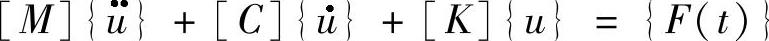
式中，[M]、[C]和[K]分别代表质量、阻尼和刚度矩阵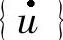，、、{u}和{F（t）}分别代表节点加速度、速度、位移和与时间相关的力。当这个有限元模型由大量自由度数量n（有限元网格节点处的位移未知）表示时，上面的矩阵具有很大规模，问题的求解可能需要占用相当多的计算资源和时间。

在这个线性动态分析的实例中（具有线性弹性材料的小位移分析模型），上面的复杂问题可以使用模态分析方法来进行求解。通过使用这种方法，可以使耦合了n个运动方程组的复杂系统简化为m个独立的（解耦的）运动方程，它们具有以下形式

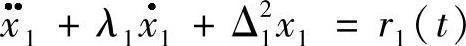
式中，λ₁和Δ²₁为特定的常数，m代表使用频率分析计算得到的内在的自然模式数量，上面的方程式对应着模式1（注意其下标为1）。对m个解耦的方程组进行求解速度会快很多，而且复杂程度也大大降低，它们的组合也提供了最初有限元模型的位移解。

模态分析需要自然频率和振动模式。为了继续进行线性动态分析，必须首先完成频率分析。

步骤12 对缓慢加载的实例（实例1）生成一个线性动态算例

生成一个名为“Slow force”的算例。【类型】选择【线性动力】，并单击【模态时间历史】，如图1-10所示。

步骤13 生成壳体、约束及网格

从之前的算例中拖入壳体定义夹具、力和网格。

步骤14 定义力

在【随时间变化】选项组中选择【曲线】并单击【编辑】按钮，如图1-11所示。

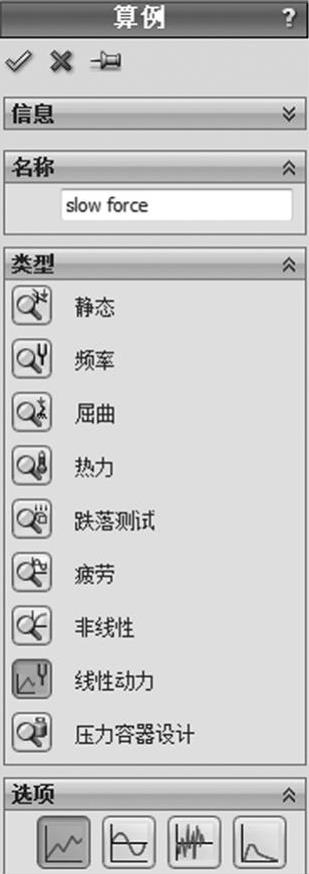
图1-10 定义算例

图1-11 编辑曲线

在【曲线信息】中，输入【名称】为“Slow”，并按照表1-1中的数值输入数据。

表1-1 输入数值表

栏目X显示的是时间（按秒计），栏目Y显示的是乘法因子，它将作用于输入在【力】值中的力，如图1-12所示。

在【时间曲线】对话框中单击【确定】，然后单击【力】PropertyManager中的【确定】。

步骤15 设置算例属性

右键单击算例“Slowforce”并选择【属性】，在【频率选项】选项卡中，输入【频率数】为5，如图1-13所示。

注意

必须强调，这里只使用了5个频率数来表示这个模型的动态特性，在接下来的章节中用户将认识到，这样低的频率值是不够的。

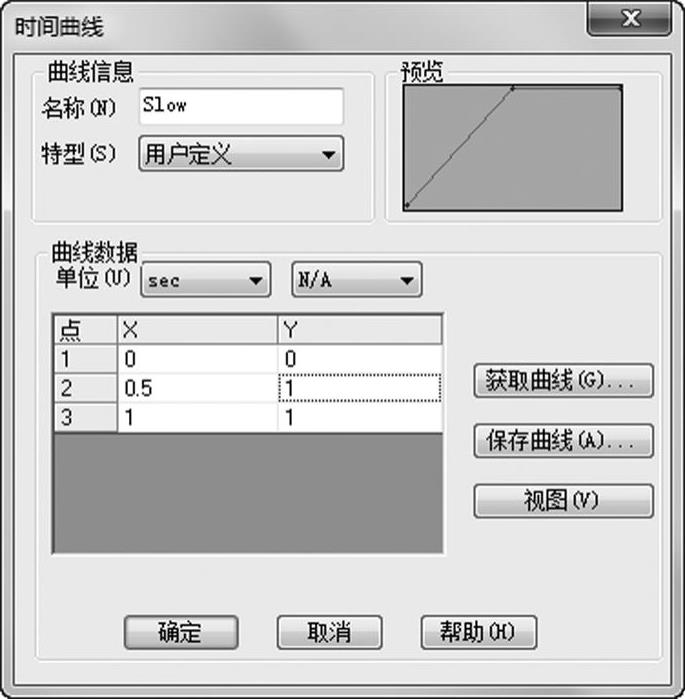
图1-12 定义时间曲线

图1-13 定义频率选项

单击【动态选项】选项卡，设置【开始时间】为0s，【结束时间】为1s。

为了输入一个【时间增量】，需要使用关于最高频率时间周期的信息。回顾前面的频率算例，计算过5个频率，而第五个频率的时间周期为0.003s。选择时间增量为用于分析的频率模式下最小时间周期的1/10左右，因此，输入【时间增量】为0.0003s，如图1-14所示。

提示

第2章将详细介绍关于时间增量的计算。(www.xing528.com)

单击【确定】。注意，增量的数量可以通过总时间除以时间增量来计算。在这个实例中，拥有3334个增量（大约等于1/0.0003）。

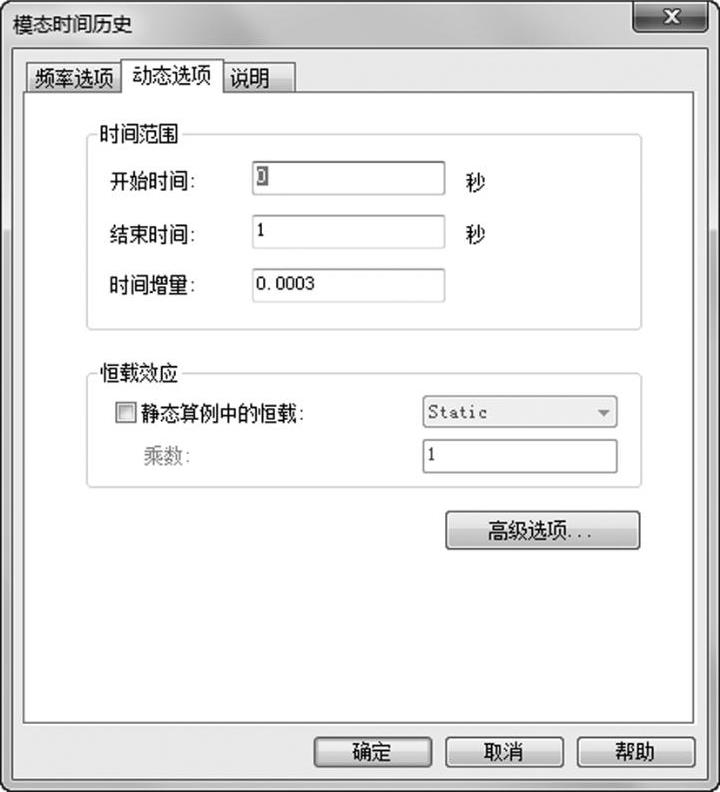
图1-14 定义动态选项

步骤16 结果选项

在算例中，右键单击【结果选项】并选择【编辑/定义】。在【保存结果】选项组中，选择【对于所指定的解算步骤】。在【数量】选项组中，勾选【位移和速度】及【应力和反作用力】复选框，选中【绝对】。在【解算步骤-组1】选项组，输入下列数据：在【步骤号】的【开始】中输入1，在【步骤号】的【结束】中输入3500，【增量】中输入10，如图1-15所示。单击【确定】。

提示

在【结束】中输入的步骤数量必须等于或大于在分析中真实时间的步骤数量。

步骤17 运行这个算例

本次运算大约需要几分钟时间。

步骤18 对缓慢加载的实例（实例1）查看其位移结果

对最后保存的时间步（334）定义【URES：合位移】图解。注意，默认情况下选择最后一个步骤，对应的时间显示为0.9993s，如图1-16所示。

加载周期末尾的最大位移为1.81mm，几乎和算例“Static”中得到的最大位移相同。原因是加载的力作用很缓慢，这也是线性静态分析最基本的假设之一。

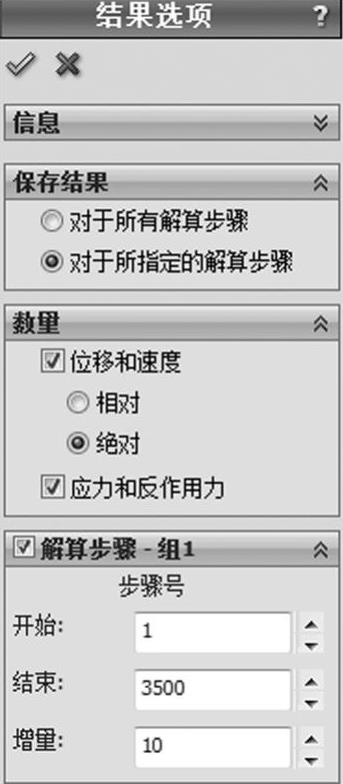
图1-15 定义结果选项

图1-16 位移结果

提示

用户可以对所有保存的时间步骤获取位移图解。

步骤19 生成末端位移图表

右键单击【结果】文件夹并选择【瞬态传感器图表】.【X轴】保持为【时间】，【Y轴】选择瞬态传感器Tip displacement，单击【确定】，生成一个响应图表，如图1-17所示。

可以看到，一旦完成载荷加载，弯管将发生持续振荡。在现实生活中，这样的振荡会因为阻尼的影响而随时间消失。因为本算例没有阻尼，所以振荡将没有衰减地一直持续下去。

步骤20 结构的最大位移

步骤18中生成的图解提供了给定时间步的位移值，之后生成的图表显示了振荡结果，它是关于所选位置的时间相关函数。然而，在所有保存的时间步中，定位整个模型的最大值也是很重要的。

图1-17 响应图表

【编辑定义】步骤18中定义的位移图解。在【图解步长】下单击【穿越所有步长的图解边界】按钮，如图1-18所示。选择【最大】并单击【确定】。

穿越所有保存的时间步长的最大位移上升了一点，达到了1.84mm，如图1-19所示。最后一个时间步（步骤18）中得到的最大位移，与从所有保存的时间步中得到的最大位移非常接近，但这只是一种巧合。一般情况下，从所有保存的时间步中得到的最大值将会明显不同。同时需要注意的是，从所有保存的时间步中得到的最大位移非常接近算例“Static”中得到的最大位移，这是因为加载的力作用很缓慢，这也是线性静态分析的基本假设之一。

图1-18 更改选项

图1-19 位移图解

讨论 前面图解中的最大位移是否为模型真实的最大位移呢？前面步骤中绘制的是从所有保存的时间步中得到的最大位移，由于设置了结果选项，只是每隔10次计算才保存一次，因此真正的最大值可能位于没有保存的步骤中。你是否能够想出一种方法，可以从所有时间步中得到最大位移？

前面图解中不能得到最大值的另一个原因可能是没有正确选择时间步，或者没有在求解中纳入足够多的保证获取准确结果的模式。这两个问题将在第2章中进行介绍。