组合凹模的有限元分析及计算方法

采用拉美公式计算即基于厚壁圆筒理论计算是假设凹模为无限长受均匀内压的厚壁圆筒，而实际生产中，凹模内壁是局部受压，载荷常为非均匀分布，凹模长度有限且常常是高度与其直径之比小于1，这与假设相差甚远，因而计算结果误差很大。有限元法计算是直接以组合凹模的实际结构及受力情况来建立计算模型，因此其不仅计算结果比较精确，而且还为组合凹模的优化设计提供了理论依据。

（1）工作应力的计算组合凹模工作应力的有限元模型如图4-46所示。

组合凹模属于典型的轴对称构件，其有限元平衡方程为

［K］｛δ｝＝｛Q｝ （4-54）

式中 ［K］——组合凹模的总体刚度矩阵；

｛δ｝——节点位移列阵；

｛Q｝——由挤压力P计算出来的等效节点力列阵。

工作应力的有限元计算程序框图如图4-47所示。

计算工作应力时，将组合凹模当整体凹模处理，即不考虑各圈材料性能的差别，假设模具为完全弹性体，其弹性模量为E，泊松比为μ。

图4-46 组合凹模工作应力的有限元模型

图4-47 工作应力的有限元计算程序框图

下面按框图顺序写出每一步的计算公式。单元截面积：

单元的平均坐标（见图4-48）：

位移函数中的各项系数，即坐标差：

a_i＝r_jz_m－r_mz_j

b_i＝z_j－z_m

c_i＝－（r_j－r_m）

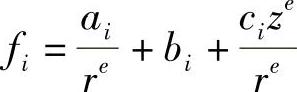
单元刚度矩阵为

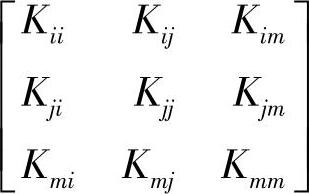
其中每一个子矩阵的表达式为

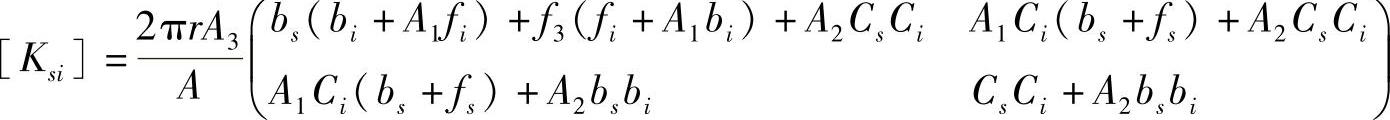
式中,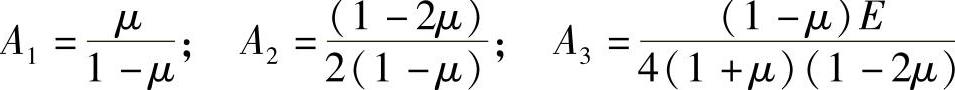

整体节点为(www.xing528.com)

［F］^e＝2πrzp_i

式中 z——内壁上节点；

i——1与i的中点和i与i＋1的中点间的距离。

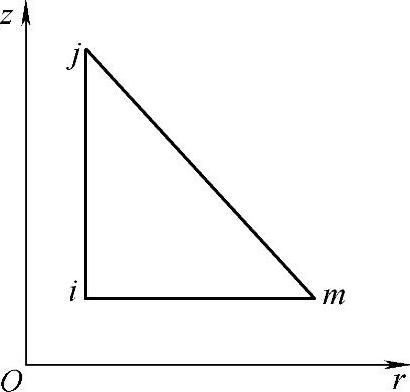
图4-48 单元坐标图

解线性方程组，求节点位移：

｛δ｝＝［K］^－1｛F｝

各单元的应变、应力分量为

式中

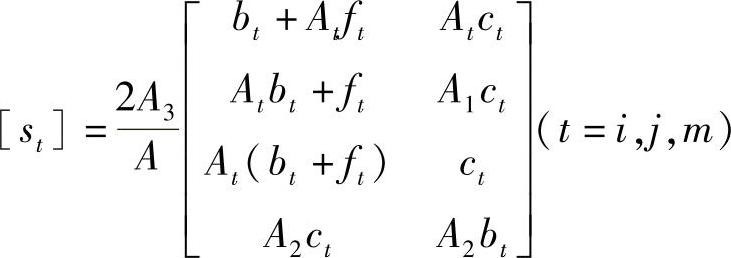
计算应力分量σ_ri、σ_ii时，对于中心区域各节点用平均法计算，即将某节点周围单元的应力值相加，然后除以单元个数。对边界上的节点则采用抛物插值法计算。

（2）预应力的计算预应力的有限元计算模型如图4-49所示。设内、外圈的刚度矩阵分别为［K^（1）］、［K^（2）］；节点位移列阵分别为｛δ^（1）｝、｛δ^（2）｝；等效节点力列阵分别为｛Q^（1）｝、｛Q^（2）｝，则两者的有限元平衡方程分别为

［K^（1）］｛δ^（1）｝＝｛Q^（1）｝

［K^（2）］｛δ^（2）｝＝｛Q^（2）｝ （4-55）

假设在装配时只有内圈被均匀压缩，由第一个方程可求出内圈中各节点位移｛δ_r^（1）｝、单元应变｛ε_ij^（10）｝和压合接触面上平均径向应力σ_r^（1），同理可求出｛δ_r^（2）｝、｛ε_ij^（20）｝和σ_r^（2）。

根据线性单元的特性，内、外圈的压缩量Δ^（1）、Δ^（2）与压合面上平均径向应力的关系如图4-50所示。由图中关系得

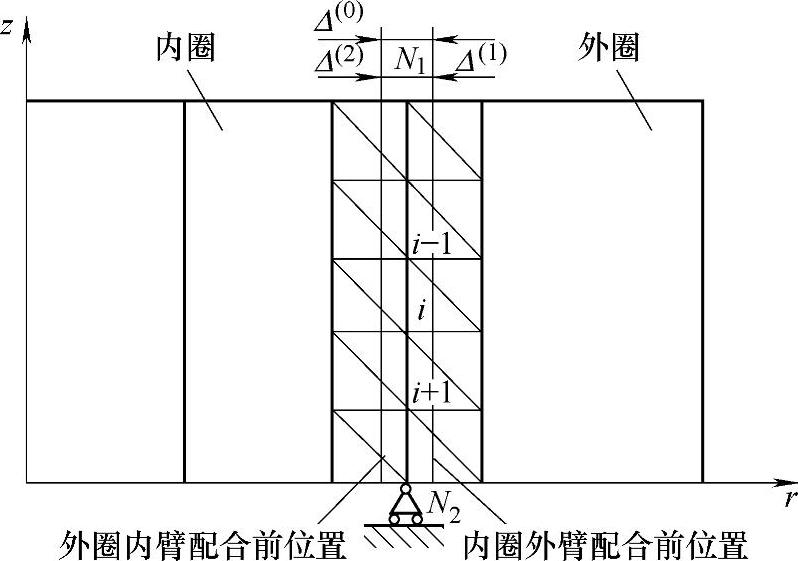
图4-49 预应力的有限元计算模型

图4-50 内、外圈的压缩量与压合面上平均径向应力的关系

仍然根据线性单元的特性，同时忽略接触面上摩擦力的影响，即认为内、外圈在接触线上同一节点的轴向位移相等，则可得内、外圈上各节点的位移和单元的应变与应力计算公式：

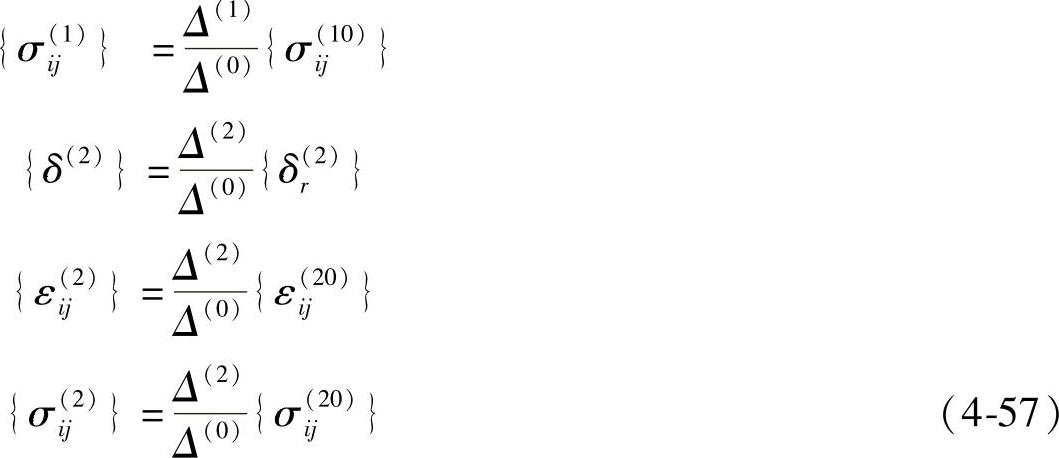
对于三层组合凹模，预应力的计算需要分两次进行：第一次计算外圈同中圈过盈配合所产生的预应力；第二次计算中、外圈组合体同凹模过盈配合所产生的预应力，然后进行叠加即得总的预应力。

分别将凹模内壁各节点上对应的预应力分量及工作应力分量相加，即可得最终的应力分布，进而计算出各节点的等效应力。以此为依据设计不同的预应力组合结构，来达到优化的目的。