优化设计：组合凹模方案优化

（1）组合凹模的受力分析与计算

1）预应力分析与计算。组合凹模受到预紧圈的接触压力P₂′_k，将产生切向预应力σ_t′和径向预应力σ_r′，两种应力的计算式为

式中，r₁≤r≤r₂（r₁、r₂分别为内、外半径）。由式（4-23）可知，σ_t′和σ_r′是压应力，分布情况如图4-42a所示。由图可知，切向压应力σ_t′绝对值的最大值产生在内壁，径向压应力σ_r′绝对值的最大值产生在外壁。凹模的外半径r₂在预应力圈的接触压力P_2k作用下缩小，如图4-42a中的虚线所示，其压缩量的计算式为

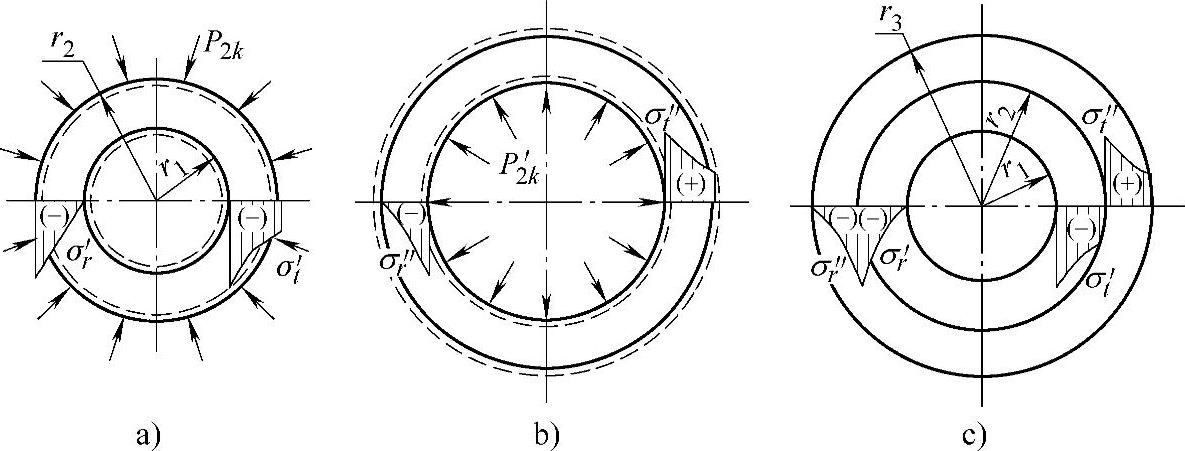
图4-42 组合凹模内预应力分布及径向位移

a）凹模内预应力分布及径向位移 b）预应力圈内预应力分布及径向位移 c）组合体内预应力分布

式中 E——弹性模量；

μ——泊松比。

预应力圈同凹模压配后，对于预应力圈而言，其接触压力P₂′_k为内压力，所产生的切向应力σ″_t和径向应力σ″_r的计算式为

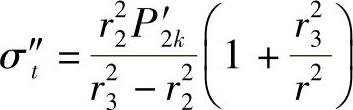
式中，r₂≤r≤r₃（r₂、r₃分别为中、外半径）。由式（4-25）可知，σ″_t为拉应力，σ″_r为压应力，其分布情况如图4-42b所示。由图4-42b可知，最大切向应力σ″_t产生在内壁，最大径向应力绝对值也产生在内壁。预应力圈的内半径r₂在P₂′_k的作用下扩大，如图4-42b中的虚线所示，其扩张量Δr″₂的计算公式为

凹模与预紧圈压配后组合体的切向预应力和径向预应力，分别等于凹模内和预紧圈内相应的预应力相叠加，其分布情况如图4-42c所示。

2）工作应力分析与计算。首先把组合凹模当作整体凹模，仅考虑由挤压力P₁所产生的切向应力σ‴_t和径向应力σ‴_r，两种应力的计算公式为

式中，r₁≤r≤r₃。由式（4-27）可知，切向应力σ‴_t为拉应力，径向应力σ‴_r为压应力，其分布情况如图4-43a所示。

3）综合应力计算。将工作应力与相应的预应力进行叠加，即可得到组合凹模内总的切向应力和径向应力。对于凹模：

σ_t＝σ_t′＋σ‴_t

σ_r＝σ_r′＋σ‴_r （4-28）

对于预紧圈：

σ_t＝σ″_t＋σ‴_t

σ_r＝σ″_r＋σ‴_r （4-29）

其应力分布情况如图4-43b所示。

（2）组合凹模的优化设计具体内容^［27］

1）凹模内壁不允许出现拉应力的优化设计。凹模常用高强度模具钢或硬质合金制造，为了防止破裂，要求在内壁不出现拉应力。在这一前提下，优化设计的目标函数是：当承受最大的单位压力时，凹模内壁不出现拉应力，而预紧圈处于许用力状态下。需优选的设计变量为凹模外径d₂、过盈量Δd₂以及预紧圈外径d₃，并满足d₃／d₂＝4～6。

①凹模外径和预紧圈外径的确定。组合凹模工作时，凹模是由内压力p₁、外压力p₂作用，如图4-44所示。P₂是组合凹模工作时的实际外压力，不等于接触压力P_2k。

按厚壁圆筒理论，可采用拉美（Lame）公式求得组合凹模内壁上即r₁处的切向应力σ_t（r₁）和径向应力σ_r（r₁）为

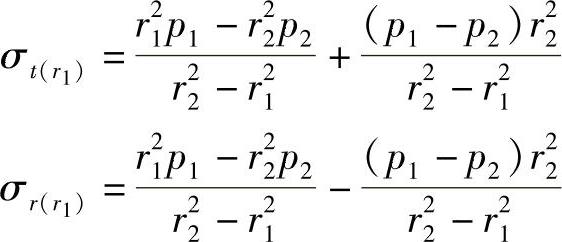
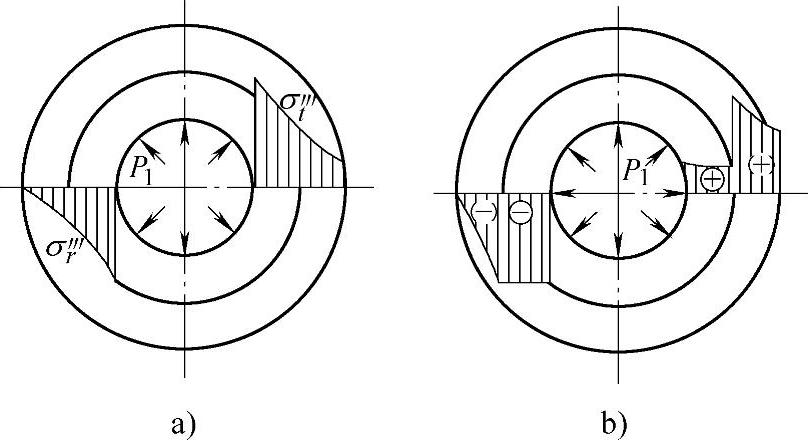
图4-43 工作应力分布情况

a）工作应力分析与计算 b）综合应力计算

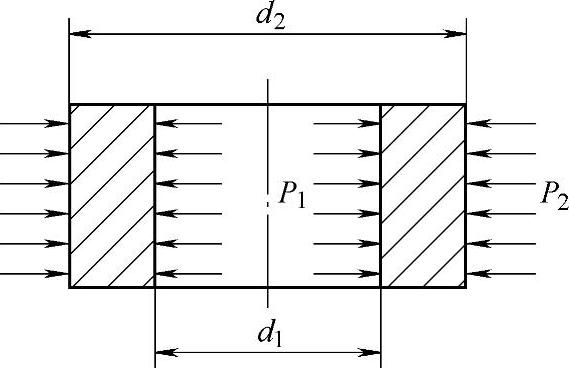
图4-44 内层凹模的受力情况

令r₁／r₂＝d₁／d₂＝m₁代入上式，得

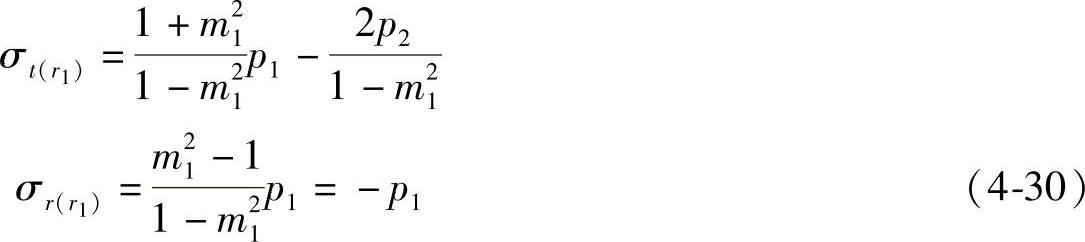
为了在内壁上不出现拉应力，应使σ_t(r₁)＝0，由式（4-30）中的第一式得

根据第三强度理论可知

σ_t（r₁）－σr（r₁）≤［σ1］

式中 ［σ₁］——凹模的许用应力。

将式（4-30）代入上式得

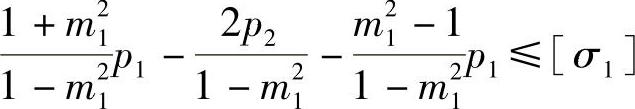
即

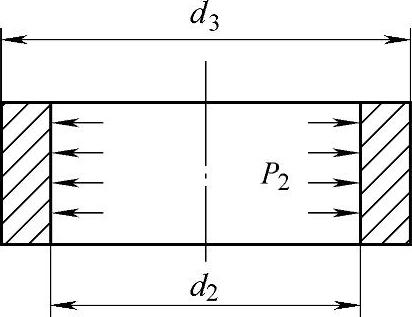
图4-45 预紧圈的受力情况

预紧圈只受内压力p₂的作用，如图4-45所示。设预紧圈的许用应力为［σ₂］，则根据式（4-32）得

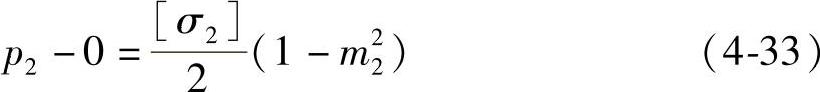
或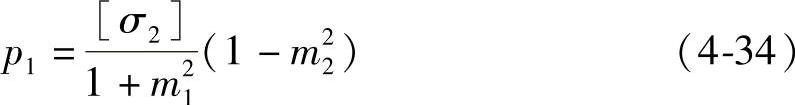

因为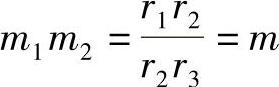，代入上式得

根据极值原理，求p₁对m₁的导数，并使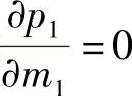，便可求出m₁的最优解：

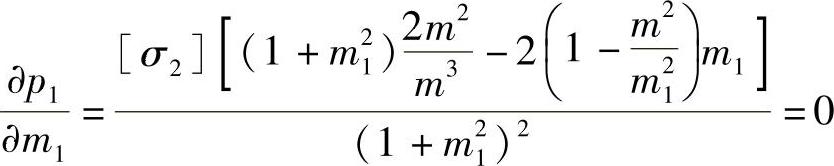
即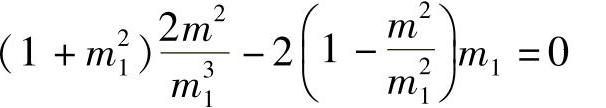

将式（4-35）代入上式得

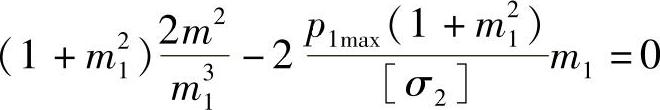
化简后，得(www.xing528.com)

将式（4-36）代入式（4-34），得

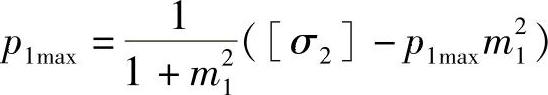
化简后，得

因此，当p₁为最大工作压力时，由式（4-37）可得m₁的最优解：

将式（4-38）代入式（4-36），得m₂的最优值：

求出m₁、m₂的最优值后，便可求得d₂、d₃。

②接触预应力p_2k的计算。作用在凹模壁上的切向应力σ_t（r₁）可由下式计算：σt（r1）＝σt＋（r1）＋σt－（r1）

式中 σt＋（r1）——凹模组合体在内压力p1的作用下所产生的切向拉应力；

σt－（r1）——凹模组合体在接触预应力p2k的作用下内壁上所产生的切向压应力。

现分别按式（4-40）计算：

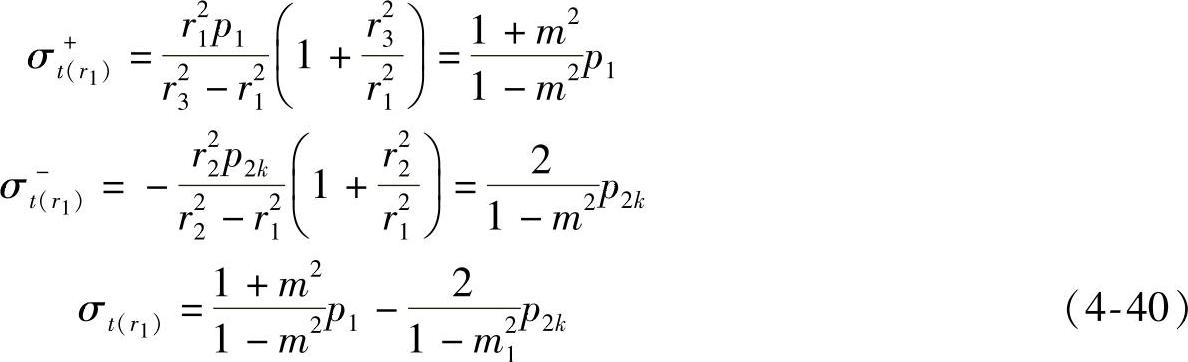
令切向应力σ_t（r₁）＝0，得

③过盈量Δd₂的计算。其计算公式如下：

式中 E——模具材料的弹性模量。

④组合凹模内壁的强度核算。凹模同预紧圈压配后，内壁上的切向压应力不能超过许用应力［σ₁］，即

σ_t（r₁）≤［σ₁］也就是

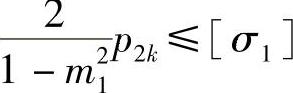
或

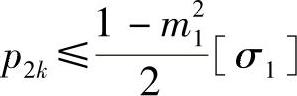
将式（4-41）代入上式并化简，得到凹模强度的核算公式：

2）凹模内壁允许出现拉应力的优化。这种情况下的目标函数是：当组合凹模承受最大压力P₁时，凹模和预紧圈正好达到许用应力［σ₁］和［σ₂］，而不考虑凹模内壁是否出现应力。约束条件是：组合凹模外、内径之比为4～6；设计变量仍为凹模外径d₂、径向过盈量Δd₂和预紧圈外径d₃。

①凹模外径d₂和预紧圈外径d₃的确定。将式（4-32）和式（4-33）相加并化简，得

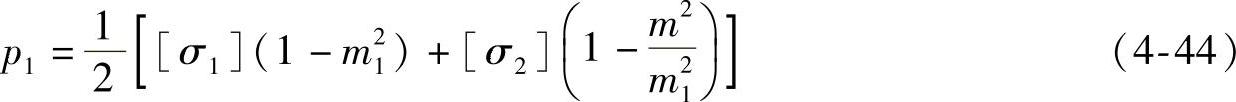
根据极值原理求m₁的最优解，即

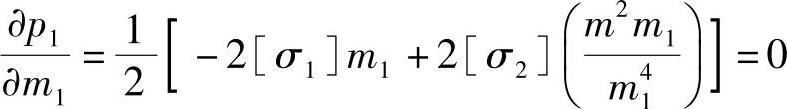
化简，得

［σ₁］m²₁＝［σ₂］m²₂

将m＝m₁m₂代入上式，得

将式（4-45）代入式（4-44），得

由式（4-46）可得最优的m₁值：

将式（4-47）代入式（4-45），并利用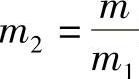就可以求出最优的m₂值。那么，最优的d₂、d₃也就可以求出，但应满足约束条件d₃／d₂＝4～6。

由式（4-47）可知，为使该式有意义，应使

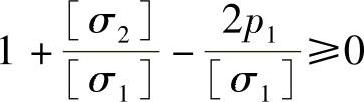
即

式（4-48）是凹模内压力P₁已知时，合理选择凹模和加强圈材料的必要条件；当已选定凹模和预紧圈材料时，也可核算凹模允许的承载能力。

②接触压力P_2k的计算。组合凹模工作时，作用在内壁处的切向应力σ_t（r₁）可由式（4-40）求得

作用在内壁处的径向应力σ_t（r₁），可参照式（4-27）得

σ_t（r₁）＝－p1（4^-50）

将式（4-49）、式（4-50）代入由第三强度理论建立的关系式，经化简得

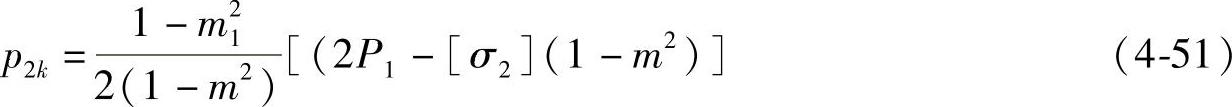
③过盈量Δd₂的计算。

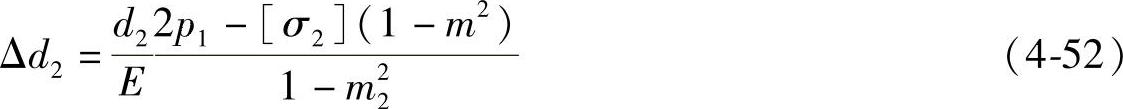
④组合凹模内壁强度计算。组合凹模压合时，其最大过盈量不能使切向压力大于许用应力，即

σ_t（r₁）≤［σ₁］也就是

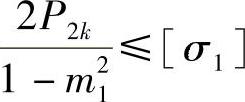
将式（4-51）代入上式得