环形毛坯尺寸计算与工艺参数优化

环形毛坯或预成形件是用于中空分流锻造终成形的工件，其尺寸计算包括已知环形件的内半径和外半径求解分流面半径、已知环形毛坯的分流面半径和外半径求解其内半径即孔半径，工艺参数的优化主要是使环形毛坯的高度h与外径d_外之比h／d_外和孔径d_内与外径d_外之比d_内／d_外都为最优。

（1）已知环形毛坯的内、外半径求解分流面半径R_分 分流面位置即分流面半径R_分的确定是研究和应用中空分流锻造原理的关键工艺参数。由环形件镦粗成形过程的特性可知，分流面的位置是随着模锻过程而变化的，因此只能求出模锻初始阶段环形毛坯的分流面半径。

图3-43所示为确定分流面主应力法示意图，根据分流面内、外两个变形区在分流面上径向应力相等，采用主应力法得到R_分的求解表达式，并经过近似处理后得到R_分的计算公式：

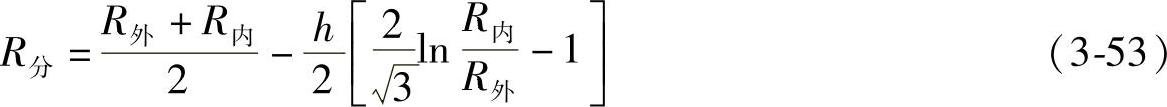
式中 R_分——环形毛坯分流面半径（mm）；

R_外——环形毛坯的外半径（mm）；

R_内——环形毛坯的内半径（mm）；

h——环形毛坯的高度（mm）。

前述工艺试验和模拟分析表明，环形毛坯在闭式模锻时，在内孔与外圆之间确实存在有分流面，由式（3-53）可计算出环形毛坯在模锻开始时分流面半径的大小。该计算结果可用于解释环形件闭式模锻过程的金属流动规律，而分流面半径的具体数值对于毛坯优化设计的作用不是太大，因此，在公式推导过程中作一些近似处理是可行的。

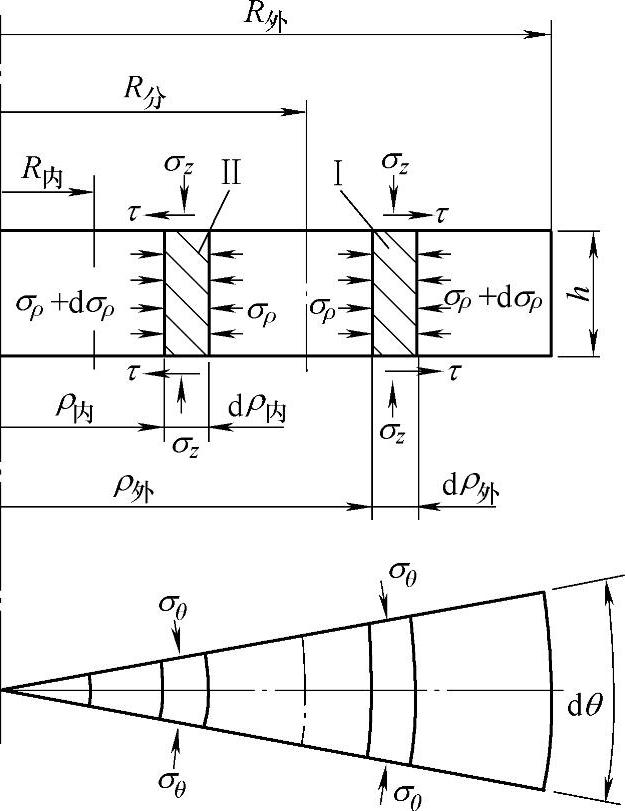
图3-43 确定分流面主应力法示意图

（2）已知环形毛坯的分流面半径和外半径求解内半径R_内^［21］ 其求解方法与求解分流面半径的方法类似，只需将分流面半径R_分 由未知数变为已知数，而将内半径R_内 由已知数变为需求解的未知数即可，其主应力法求解示意图与图3-43相同。因式（3-53）是作了较多的近似处理所得，若同样采用较多的近似处理来推导出R_内，会导致环形毛坯内半径R_内 误差过大而得不到优化值，因此，需进行严格的推导并得到以下公式：

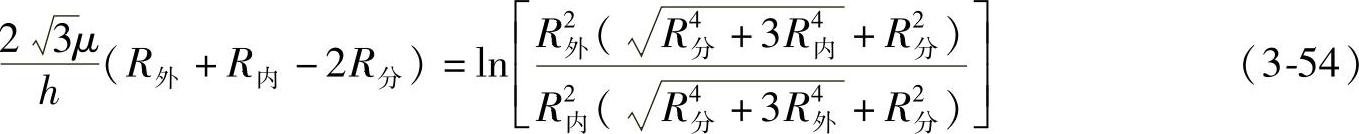
式中 R_分——环形毛坯分流面半径（mm）；

R_外——环形毛坯的外半径（mm）；

R_内——环形毛坯的内半径（mm）；

h——环形毛坯的高度（mm）；

μ——摩擦系数。(www.xing528.com)

由相关的数学知识可知，式（3-54）是一个超越方程，很难进一步演变为R_内 的计算表达式。因此，本文提出基于Matlab软件采用计算机编程的方法来求解。

设定a＝R_外，b＝R_分，u＝μ，t＝R_内，所编函数m-文件funx.m如下：

function fx＝funx（t）

a＝输入数值；

b＝输入数值；

h＝输入数值；

u＝输入数值；

fx＝2^∗sqrt（3）^∗u／h^∗（a＋t-2^∗b）-log（（a^∗a^∗（sqrt（b＾4＋3^∗t＾4）＋b^∗b））／（t^∗t^∗（sqrt（b＾4＋3^∗a＾4）＋b^∗b）））；

所编算法文件solver.m如下：

t＝fzero（′funx′，1，optimset（′Display′，′off′））

首先，打开Matlab软件，将funx.m文件置入Matlab的工作目录下或者指定Matlab的工作目录到funx.m文件的目录下，然后在Matlab软件中打开funx.m文件，在funx.m里输入相关参数数值，最后在命令行输入solver命令，即可得到t的解，即所求环形毛坯的内半径R_内 的值。

（3）环形毛坯h／d_外 与d_内／d_外 的优化值^［21］ 要求解h／d_外 与d_内／d_外 的优化值，可通过两种方法：第一种方法是以获得合格的圆盘形直齿轮精密锻件的前提下模锻成形力最小为目标函数，以毛坯外径d_外 与齿轮根圆直径d_根 相等即d_外＝d_根，0＜d_内／d_外＜1为约束条件，以h／d_外 和d_内／d_外 为优化的设计变量建立数学模型，采用修正的序列二次规划法（SQP）求解，但这种方法求解过程复杂、难度大。

第二种方法即本文所采用的方法，仍以模锻成形力最小为目标，根据闭式模锻成形工艺知识及经验，对于同一锻件，假设多组d_外、d_内 和h数据，采用刚塑性有限元法和图3-39所示的有限元模型及其算例，在保持各环形毛坯体积V_环 相等和外径d_外 不变的条件下，通过模拟计算得到不同的h／d_外 和d_内／d_外，即不同的h与d_内 时相应的成形力P_i，则其中最小的P_min所对应的h／d_外 和d_内／d_外 即为所求的优化工艺参数。

表3-24 优化工艺参数及结果数据

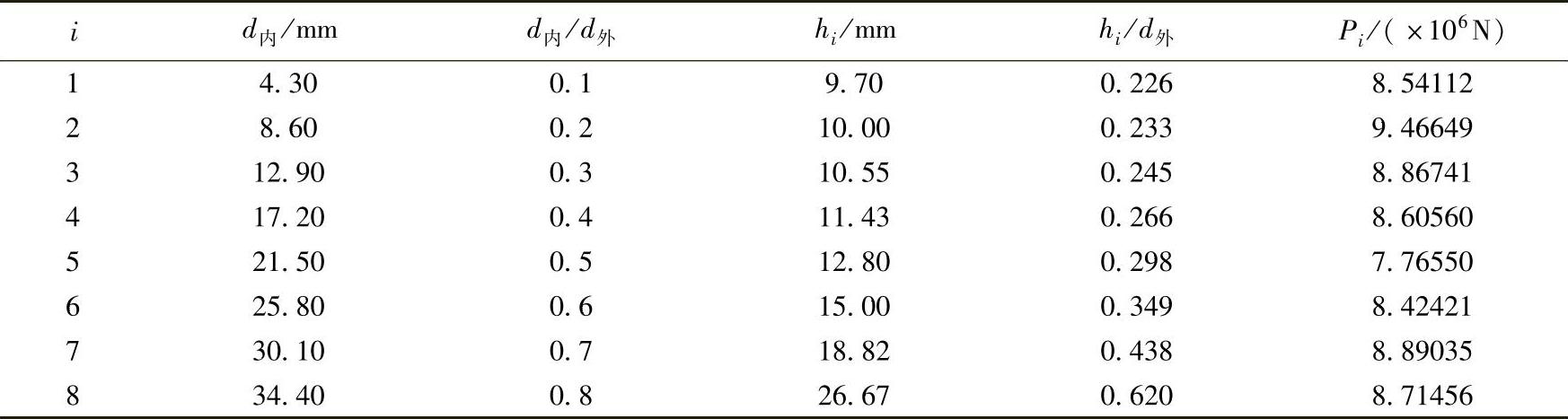
由表3-24所列计算结果可知，最小的成形力为P₅，则P₅所对应的d_内5／d_外＝0.5和h₅／d_外＝0.298即为图3-38所示的直齿圆盘齿轮的环形毛坯尺寸的优化值。经实践表明，这两个比值对于结构相似的直齿圆柱齿轮的环形毛坯设计具有参考意义。