分析与计算：多余金属分流过程

毛坯多余金属分流与在模膛内成形构成整个闭式模锻的成形过程。对其过程进行分析与计算，可以为获得闭式模锻成形规律和工艺参数的确定提供理论依据。

下面着重对两种应用较多的饼盘类锻件的分流形式——纵向分流和中心孔分流的分流过程分析与计算进行详细论述。

（1）纵向薄飞边分流过程的分析与计算

1）纵向薄飞边分流过程中模膛受力分析与计算。纵向薄飞边分流系统如图3-31所示。

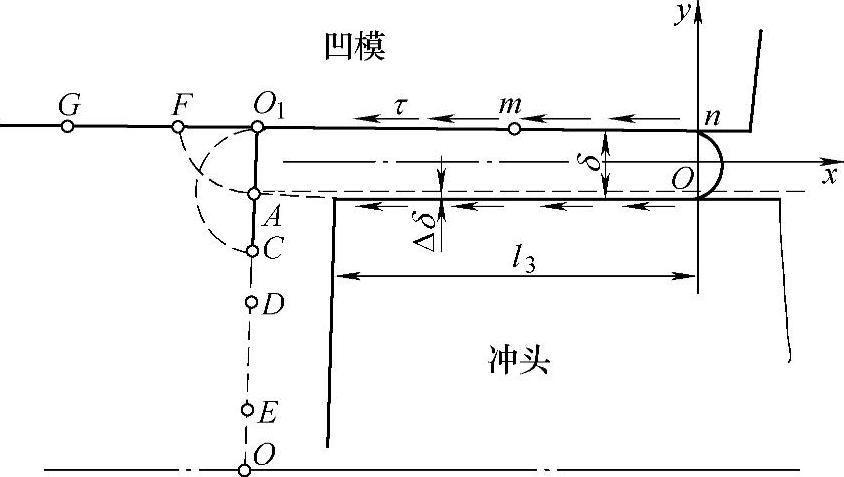
图3-31 金属在凸凹模缝隙中的纵向薄飞边分流系统

当模壁上摩擦达到最大，闭式冲孔或闭式反挤压和镦粗结束时多余金属被挤入凸凹模间端部的缝隙中，此时模具受力最严重，且同纵向飞边接触的模壁上作用的正应力呈非均匀分布。其相对正应力分布规律为

式中 x——从点n到研究点的距离（见图3-31）；

δ——凸凹模间的间隙值；

K——材料常数，即材料屈服时的最大剪切应力。

在纵向飞边根部附件的模壁（y向）上的径向应力为

式中 l₃——纵向飞边的长度（见图3-31）。

如图3-31所示，可以认为在A点附近的金属处于塑性状态，并在缝中沿x轴向流动，从O₁点到凸模端面滑移线的转角等于π，滑移线弧近似于半圆。由A点描述的和由中心描述的一样，可由公式（3-35）和在具有粗糙模底的模膛中镦粗时模底中间部分的相对切向应力公式：

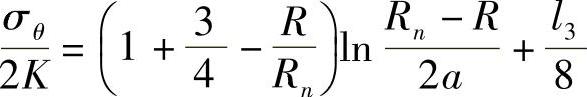
可得，该点附近范围内的相对径向应力分布公式：

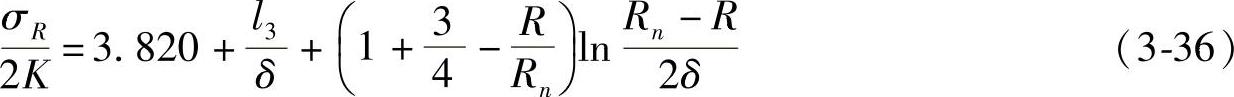
式中 R_n——锻件半径（mm）；

R——从研究点到对称中心线的距离（mm）。

l₃——飞边长度（mm）；

δ——凸凹模间隙即飞边厚度（mm）。

对于低锻件的镦粗且在狭缝中形成纵向飞边时，作用在凸模端面上的单位压力同镦粗高锻件一样按以下公式确定：

在AC部分（见图3-31）

σ_R＝2Kψ

在CD部分

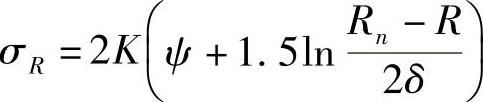
在DE部分

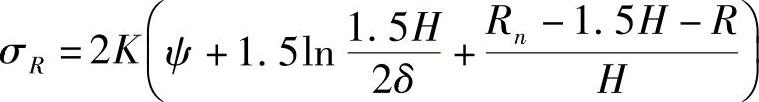
在EO部分

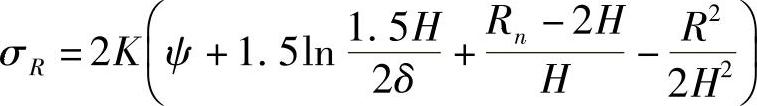
镦粗时冲头端面上的法向应力图如图3-32所示。

在C点的非均匀法向应力，通过公式（3-35）和具有旋转角π的滑移线确定。该点附近的边界条件取决于纵向飞边的长度与宽度之比，这个比值对法向应力的大小有重要影响。

以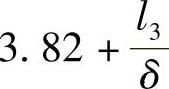代替前式中的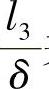并经数学处理后，可得闭式模锻时的单位压力：

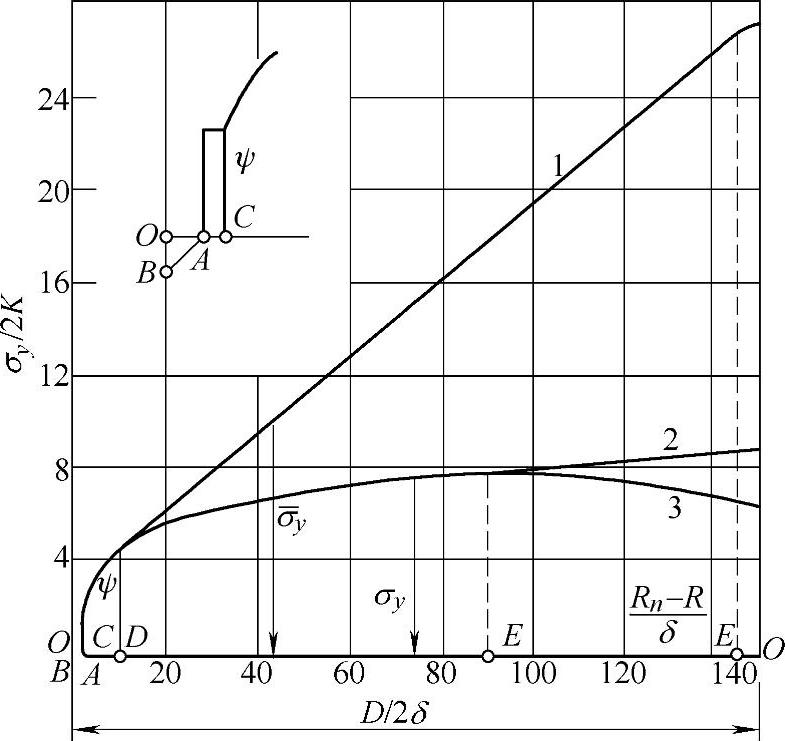
图3-32 镦粗时冲头端面上的法向应力图

1—低锻件（H／D＝0.02） 2—高锻件（H／D＝1）不考虑冲头端面中心摩擦的降低 3—高锻件（H／D＝1）考虑冲头端面中心摩擦的降低

对于高锻件

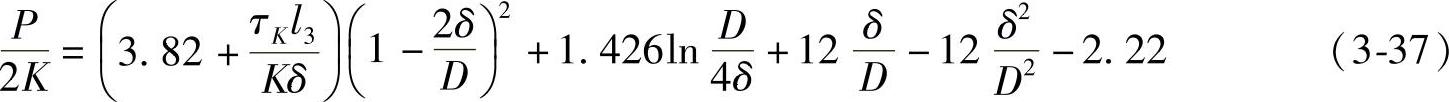
对于低锻件

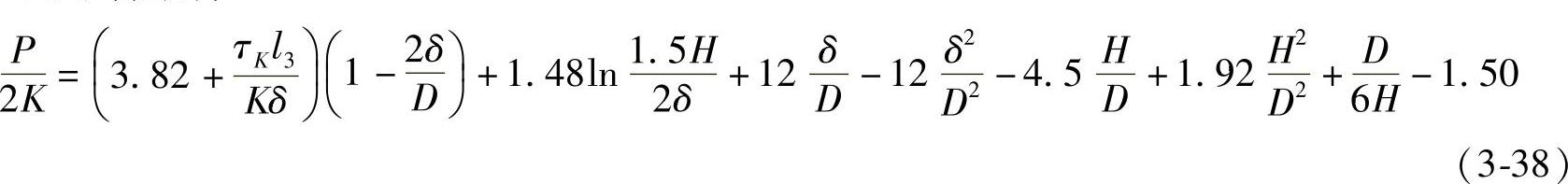
由式（3-37）和（3-38）可以看出，在闭式模锻中，当有多余金属从凸凹模间隙中挤出时，单位成形力的大小同端部纵向飞边的相对厚度δ／D成比例，单位压力的相对值P／2K常达20～25。

在闭式或半闭式模锻中，坯料上所有多余金属从凸凹模端部缝隙中挤出时，凹模可能没有特别过载，而凸模有可能大大超载，这取决于变形金属的力学性能。这种情况下，凸模可能发生塑性变形或破裂。

通过对有多余金属挤入端部缝隙中的闭式冲孔和模锻的分析表明，当锻件直径D与冲头直径D_b之比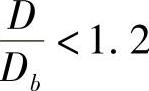时，模膛中的单位压力急剧上升。如果变形材料为高强度金属或合金时，模具将被很快地磨损而失效。当用这样的材料通过闭式冲孔得到空心杯形件时，若D／D_b＜1.25，可借助复合工艺成形，即先闭式冲孔到D／D_b＜1.25，接着反挤到规定的壁厚。

闭式模锻高锻件时，在端部粗糙的冲头上的平均相对单位压力为

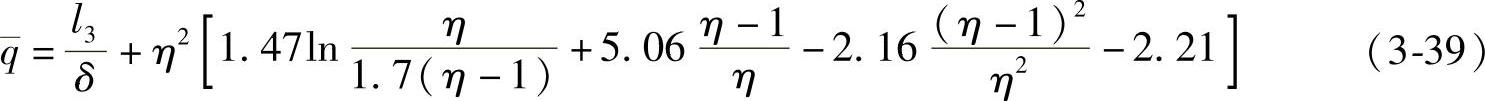
式中 l₃／δ＝2.85或2.57，取决于冲头端面的摩擦条件。

边界轮廓和摩擦条件的某些变化对单位压力的影响不大，因此所有的计算可按式（3-39）进行。

图3-33所示为闭式冲孔开始时单位力的变化曲线。该曲线表明，在冲头上的单位压力取决于凹模与冲头的直径之比和冲头端面上的接触摩擦。

由图3-33可以看出，当D／D_b＞1.30时，单位压力的吻合程度实际保持不变。当模膛中摩擦等于零（曲线1）时，相对单位压力不超过2.90；当模膛中的摩擦达到最大（曲线2），相对单位压力为3.20。当D／D_b＝1.09时，相对单位压力达3.5～4.0。随着直径比的进一步减小，无论摩擦为零还是达最大，相对单位压力强烈地增长，当摩擦达到极限值时，力的差别达19％。

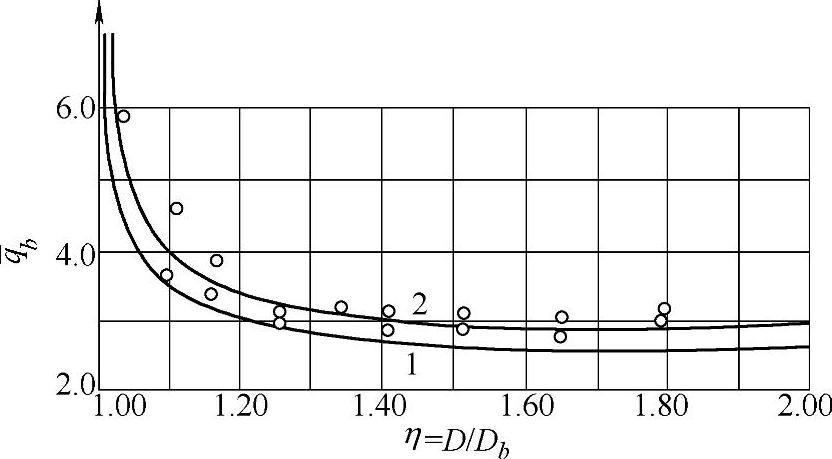
图3-33 闭式冲孔开始时单位力的变化曲线

1—摩擦力零时 2—摩擦力达到最大时

当对杯形件进行反挤成形时，随着筒壁长度的增长，由于与冲头侧表面接触摩擦力增加而使模锻力增加。摩擦力可按下式计算：

T＝πD_bl₃τ_k

在冲头上所引起的非均匀单位压力为

则冲头上总的单位反挤压力为

因此，对于闭式冲孔或反挤压，金属同冲头的接触长度为l₃时，冲头端面上的单位压力可通过式（3-40）和（3-41）计算确定。为了得到均匀一致的筒高和适当的外圆半径，必须施加附加作用力，即使毛坯金属处于封闭状态下最终成形，这时所需的成形力还需考虑作用在筒顶边缘的精压整形力。

2）纵向飞边变形过程的分析与计算。当在工作速度较高的设备上进行闭式模锻时，即使模膛尚未充满，在冲头与凹模之间的缝隙中也能形成很薄的纵向飞边（见图3-31），且这个端部飞边可能处于弹塑性状态。如果缝隙宽度均匀，那么靠近飞边边缘部分的变形将是弹性的。根据卸载原理，当塑性变形结束后，材料将出现弹性回弹，使飞边金属紧压在模膛上而引起摩擦力。

在实际模锻中，特别是当模具有两个分模面时，通过闭式冲孔或反挤可得到高度较大的空心锻件。在这种条件下模锻时，在凸凹模之间的缝隙中挤出的飞边边缘附近的相当部分金属常处于弹性状态，而其流动过程与两个平行粗糙平板间挤出的薄层金属的变形过程相似。对于这种情况，其弹塑性的基本方程为

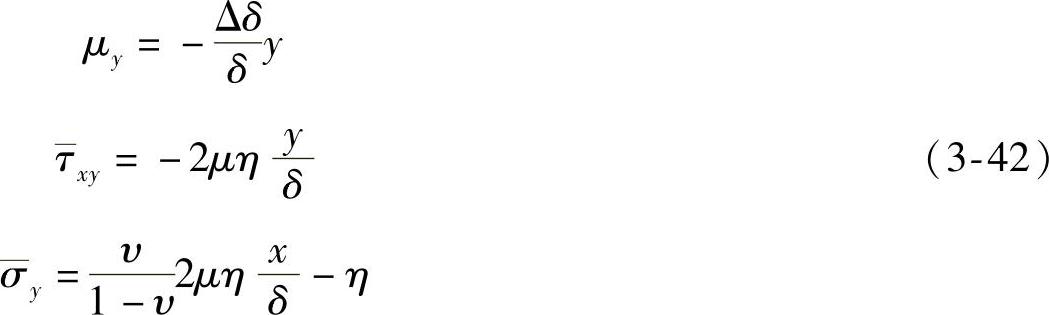
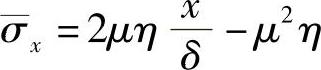
式中 Δδ——模膛缝隙段模壁的位移（见图3-31）；

η——靠近边缘（在n点）的非均匀法向应力，；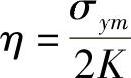

υ——泊松比。

利用式（3-42）确定飞边中塑性区和弹性区的边界时，需假设位移u_y仅取决于y坐标轴。因为这样假设，区间边界将平行于x轴。(www.xing528.com)

离弹性和塑性流动区边界的相对距离可用式（3-43）确定：

式中 y_δ——被确定区域边界的纵坐标。

随着摩擦的减小，在区间边界n点上的压力自飞边的对称轴（即x轴）移向模壁。当变形金属由模膛挤出而形成飞边的纵向流动时，靠近模壁附近的金属便于实现塑性变形。当无摩擦时，变形所需的压力等于流动应力。当摩擦达最大时，变形所需的压力为流动应力的1.22倍。然而当模膛加工精度过低且飞边金属处于较软化的状态时，变形金属同模具有可能出现粘着现象。在这种情况下，塑性变形将扩展到整个飞边壁厚。当摩擦最小时，如果在n点（见图3-31）的压力不小于流动应力的话，那么当摩擦达最大时，其压力将不会小于流动应力的1.33倍。

在模壁上切向应力达最小值（－K）的点的横坐标，可用式（3-45）确定，但需取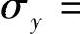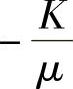、υ＝0.5，得到结果为

可见，在这点必须允许切向应力函数从－μσ_yn到－K。如果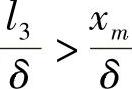，则在该点的法向应力为

通过式（3-42）和（3-45）可以建立端部缝隙处模壁上的法向应力分布曲线。为了将应力曲线由与飞边对应的模壁端延伸到与工件对应的模壁，可采用由A点到F点的滑移线场（见图3-31），如果滑移线为摆线，那么Q₁F＝1.29δ。采用汉基方程，便可确定F点的法向应力。

金属自F点向端部缝隙和模底分散流动，其法向应力为

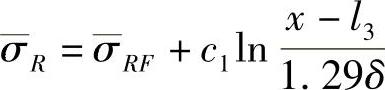
式中 c₁——常数，c₁＝1～1.48；

σ_RF——在F点的非均匀法向应力。

自分流点到模膛底部应力逐渐降低。

如果模膛底部角隙没有充满，能够较容易地建立从未充满的角隙沿着模壁到分流点的法向应力曲线图。如果在模底角隙已充满，那么在绝对刚性的模具接触面上的应力就难以确定。对于绝对刚性的锻模，可认为其模底和模壁随模膛中压力的增加而移动。由于靠近分流点附近的变形金属沿模壁随冲头向下流动，模壁上的切向应力可采用相等的K值。

分流点的位置建议按式（3-46）确定：

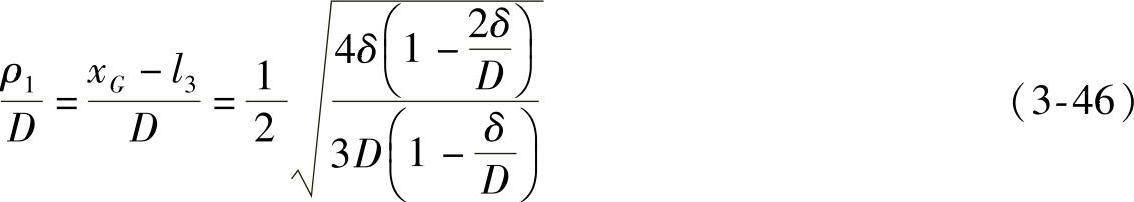
式中 x_G——在模壁上分流点的坐标。

如果变形金属能相对于模壁移动到模底，那么靠近分流点的应力可采用式（3-47）确定：

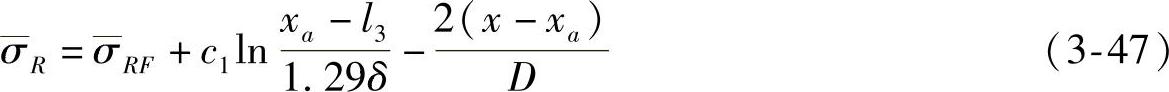
式中 x_a≤x≤H＋l₃。

由此可见，法向应力取决于接触面上的摩擦和挤入缝隙中的飞边长度。

3）合适的凸凹模间隙及飞边应力曲线。根据生产实践，在卧式机械压力机上用闭式或半闭式模具模锻直径为20～30mm的零件时，合适的凸凹模间隙为0.2～1.0mm；挤压直径为100～250mm的零件时，挤压凸模与凹模工作筒的合理间隙为0.1～1.0mm。两者的间隙与锻件直径的比值分别为0.01～0.033和0.001～0.004。

当在锤和立式机械压力机上进行闭式和半闭式模锻时，其凸凹模间隙的相对尺寸同上述挤压时的相对尺寸一样。所以模膛内的应力状态及飞边形成过程相似，但模具受力条件要差一些。

为了分析现有闭式模锻的工作并确定其作用力，我们取中等间隙值并建立计算图表（见图3-34），在图表中标出试验点。计算结果同试验数据有相当好的吻合程度。因此，如果缝隙中的一部分飞边金属处于弹性状态，那么所用的计算方法能够确定在给定方向上的侧向力。

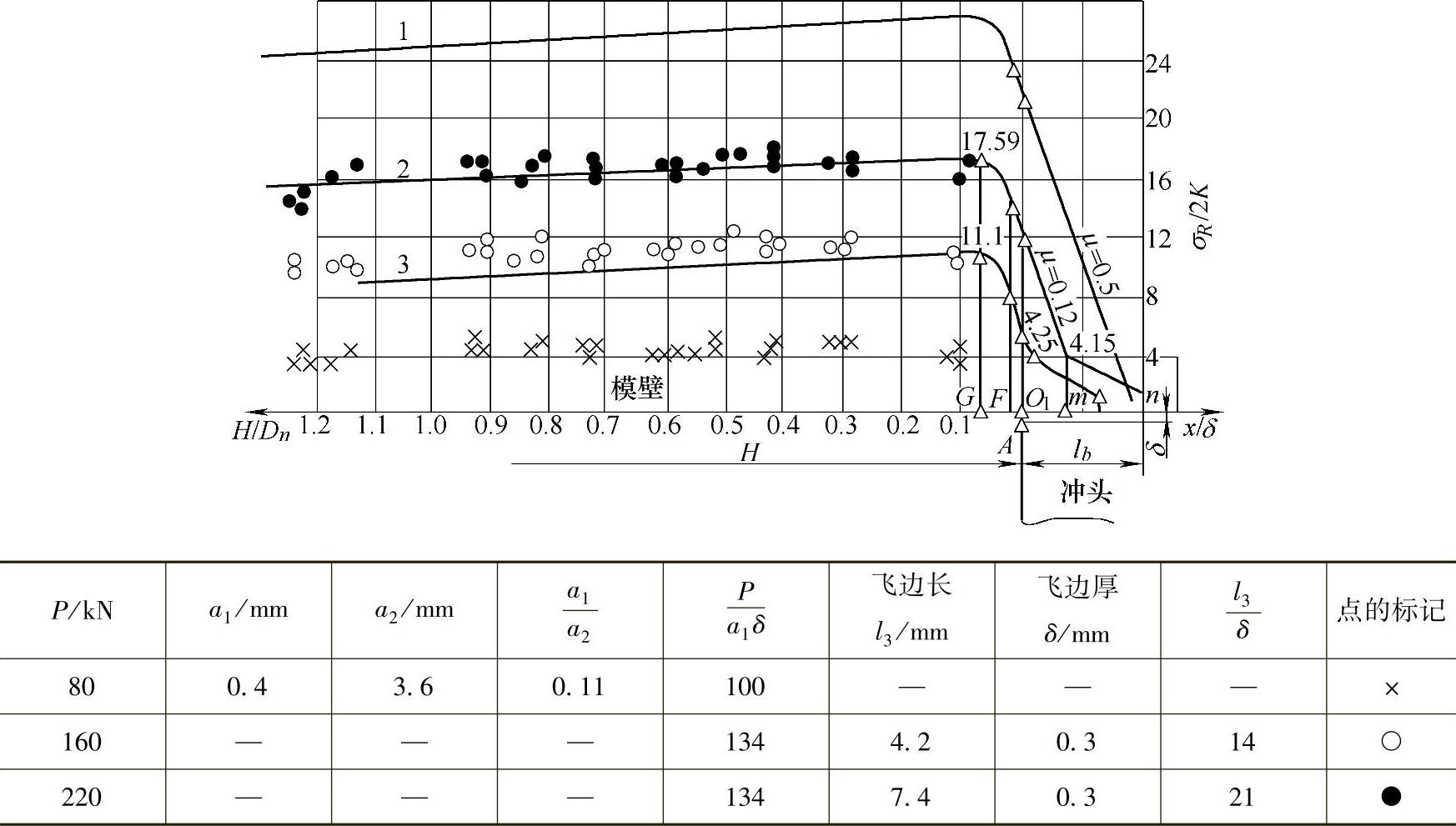
图3-34 当在狭窄缝隙中挤出金属时模壁上的法向应力曲线

一般地，开始形成纵向飞边时，被动角即模底角的圆角半径可以清楚地测量出来，所以，可利用近似的动力学方法即按式（3-46）可以求出金属沿模壁分散流动的界限。

图3-34中的法向应力曲线是按式（3-34）及其他公式建立的。其中，曲线1为凸凹模缝隙中的摩擦达最大时的应力分布情况；曲线2和3为缝隙中摩擦最小（μ＝0.12）且模壁无斜度时的应力分布情况。

曲线1、2适用于相同的模膛参数和端部飞边尺寸，但曲线1是在接触面上摩擦达最大并假定整个飞边处于塑性状态时所获得的，而曲线2是μ＝0.12并假设飞边边缘及中部的金属处于弹性状态下获得的。

由图3-34可见，理论计算的曲线进行对照表明，随着端部缝隙（曲线1、2）摩擦和端部飞边长度（曲线2、3）的增加，模壁上的法向应力剧烈地增加。法向应力的试验点分布与计算曲线2、3（μ＝0.12）的变化相符合，对应的飞边相对长度分别为21和24。

还可以看出，图中闭式模的主动角隙事实上就是凸凹模间隙端部的缝隙。当充满角隙而未形成飞边时，其非均匀应力的相对值等于4～5，所施加的作用力为80kN；当飞边相对长度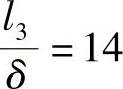时，非均匀应力相对值等于11～12，所施加的使用力为160kN；当相对长度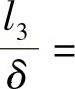时，应力相对值为16～18，所施加的作用力为220kN。当模壁被加工得很精密、μ＝0.12时，为了得到轮廓清晰并具有圆角半径为δ的锻件时，必须在模壁上建立起单位压力4～5倍的压力。这就是图3-34附表中的第二种情况，即飞边长为4.2mm，所引起的压力为材料屈服极限的2～2.5倍以上。

作用在冲头上总的单位压力等于作用在冲头顶端面上的力和作用在其侧面上的摩擦阻力之和。

在等宽度缝隙中接触摩擦达到τ_K时的切向应力取决于表面粗糙度和靠近边缘的压力，如果用式（3-42）中的第二个方程来描述，并假定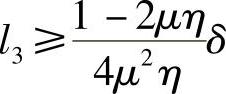，那么，单位压力的绝对值为

式中 q_m——由冲头侧面的摩擦引起作用在飞边边缘的横截面上的单位压力；

D_b——冲头直径；

x_m——边缘到m点的距离（见图3-34）。

如果沿整个飞边长度上的摩擦达到最大，那么在式（3-48）中第二项等于零，因为x_m＝0。如果不存在最大摩擦的区段，即l₃－x_m＝0，那么单位压力仅取决于括号中的第二项。

为了减少凸凹模间摩擦力的影响，即降低ψ_n值，凹模的深度比坯料经镦粗之后的高度超过3～5mm。如果锻件沿高度没有径向定位的话，则冲头孔具有导向护圈，即冲头端部的工作带，工作带相对于冲头杆部直径高出0.3～0.5mm。在冲孔或反挤压时，变形金属同凹模壁的接触长度随冲头挤入深度的增加而增加，剩余长度l′₃＝Δh（3～5）mm，而冲头同变形金属的接触能够超过工作带的长度。

冲头端部表面应当同零件底部形状相同，如果允许作成任意形状，则应作成锥形，而锥形外形应与刚塑性边界上的滑移线形状相适应。

4）变形金属被挤入凸凹模端部缝隙时所产生的侧向力。被挤入凸凹模端部缝隙中的飞边金属紧贴在凹模壁上，随着飞边长度的增加，导致侧向力和主方向成形力的增加。侧向力和成形力随飞边同模壁接触面的增加而增大。

当端部缝隙中摩擦达最大时，作用于锻件轴向剖面上的侧向力按式（3-49）确定：

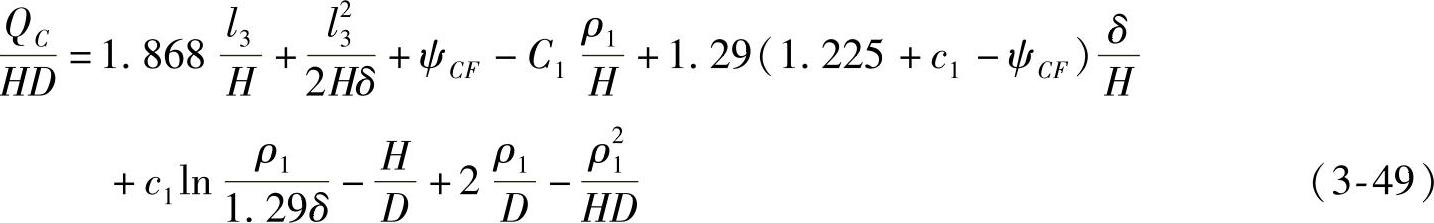
式中 Q_C——归于流动方向的侧向力；

D——锻件直径；

H——锻件高度；

其余符号如图3-31所示。

此时，在F点的非均匀应力为

如果在端部缝隙中基段x_m上的摩擦小于最小值，则侧向力由式（3-45）等得：

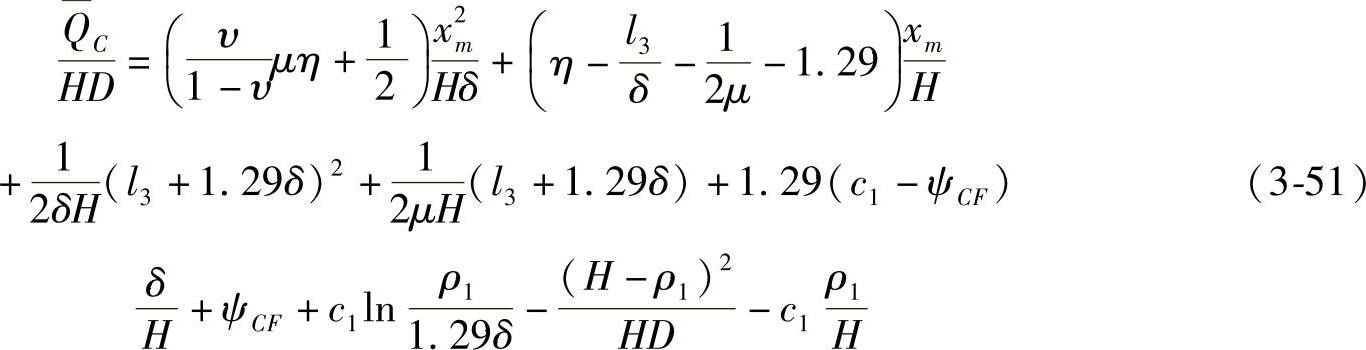
式中，ρ₁的大小按式（3-46）确定。

在F点的非均匀应力与式（3-47）和（3-48）相符：

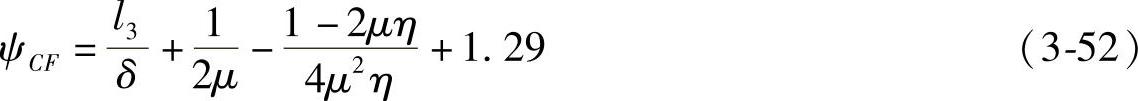
以上各式中的Q_C为相对侧向力，总的绝对侧向力应为求得的结果乘以锻件轴向剖面面积HD和在给定温度下材料的流动极限。

（2）横向薄飞边分流过程的分析与计算 为了检查从环形侧向分流腔中挤出多余金属而形成薄飞边时对单位压力变化的分析结果，进行了以下试验。试验模具的结构如图3-35所示，模壁经粗加工，侧向缝隙高度可在0～3mm的范围内调节，每次调整后就固定不变，冲头和下模芯端部表面光滑，模膛直径D＝50mm，侧壁上装有带探针的指示器（见图2-29）。当铅柱试样置于凹模内被压缩至充满模膛时，试样下端的金属被挤入侧向缝隙中，随着金属从模膛中挤出，指示器探针被压缩，所表示的大小为（D_n－D）／2，同时可读出力的大小。铅柱试样直径为ϕ30mm，长度分别为60、32、18mm，相应的流动应力分别为σ_s＝3.2、3、2.9MPa。当飞边宽度达10mm时，对应的最大比值D_H／D＝1.37。试验中，飞边厚度h在1.5～2.5mm之间变化。所得单位压力q和不同锻件的高度与其直径比R_H／R_n的关系曲线如图3-36所示。

因为保持在所有情况下挤出的飞边金属体积相等，故当H_K＝20mm、10mm、4.5mm时，试样最终的高径比为H_K／D＝0.4、0.2、0.09。这表明了不同的锻件高度和在模壁上不同的摩擦的影响。

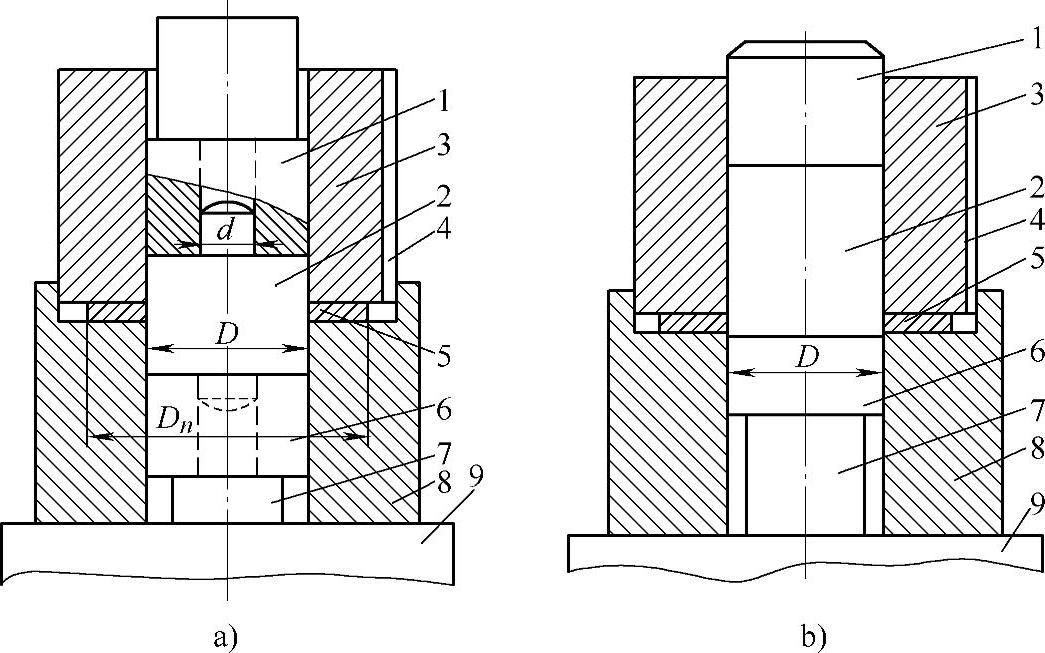
图3-35 环形缝隙式发流器试验模

1—冲头 2—锻件 3—圆筒 4—防转槽 5—环形分流器 6、7—固定模芯 8—模座 9—垫板

由图3-36中曲线的变化可以看出，变形力随着金属挤入侧向缝隙中飞边宽度的增加而增加。

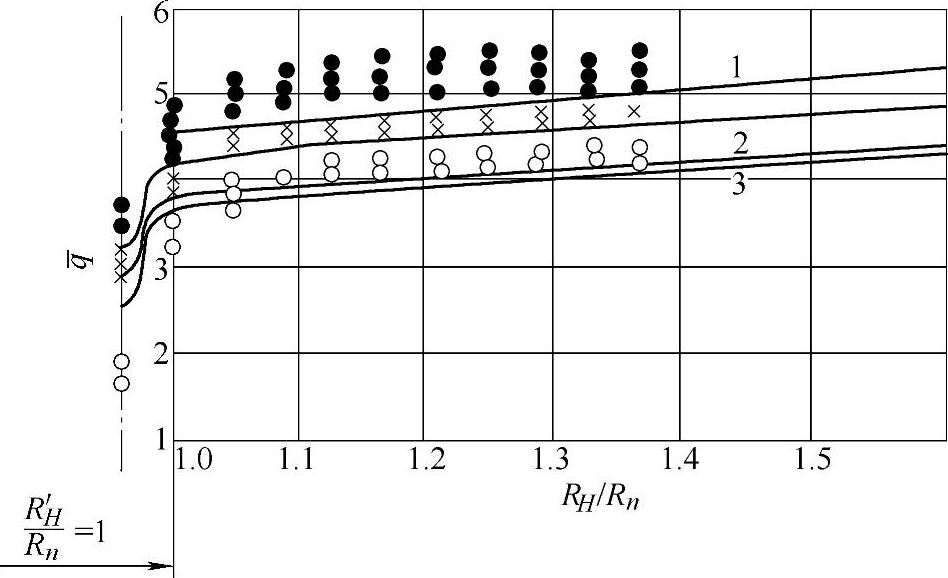
图3-36 金属从环形侧缝中挤出时单位压力的变化

在飞边边缘的表面上有时出现滑移线，类似于拉延平整度不高的板料时所出现的现象。这对分析侧向薄飞边的应力状态有重要的意义。

尽管冲头同凹模配合严密，但铅还是流入到凸凹模端部的缝隙中，这是当试件被压缩到高度为H_K＝20mm，纵向飞边厚为0.2～0.3mm，宽达10mm时发生的。金属流入端部缝隙中，促使模壁上的摩擦力增加并导致更大的侧向力，高试件模锻时尤为显著，结果使得冲头与凹模间的间隙增大。

低试样（H_K＝4.7mm）变形时，理论计算的曲线与试验点相符合；高试样变形时，两者的吻合程度较低。这个差别可用两点理由来说明：第一，当薄的端部飞边发生塑性变形时，促使试样同模具的侧向接触面积增大，因而阻碍冲头对试件金属的压缩；第二，对于高度尺寸大的试样，变形大而又不均匀，消耗在内部的剪切应力上的功更大。