闭式模锻力除了利用上述公式计算外,还可利用分块法求解,即根据锻件的变形特点和变形区划分情况分别计算各块的变形力,然后叠加即可求得总的变形力。例如:
1)对于锻件中心部分圆角半径等于或略大于外圆角半径的变形(见图2-15g),模锻力等于充满角隙的力与镦粗辐板的力之和。
2)对于中心部分圆角半径大于外圆角半径的变形(见图2-47a),模锻力等于充满角隙的力与中心部分多余金属被挤出的力(这部分挤出力与开式模锻本体部分的变形力的求法相同)两者之和。
3)形成纵向飞边才能充满角隙时(图2-47b),成形力等于飞边区变形力与多余金属挤出模膛(这部分与开式模锻时本体部分变形力的求法相同)两者之和。
下面以变厚度圆形锻件(见图2-47)为例,说明用切块法计算其闭式模锻力的过程。
当闭式模锻该变厚度圆形锻件时,可将其划分为两部分来分析:直径为d的中心部分的半闭式镦粗和宽度为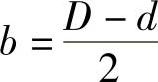 的圆环闭式镦粗。
的圆环闭式镦粗。
为了确定正应力,只需确定半个轴截面上的应力分布即可。
锻件圆形部分的接触正应力可分为三个区:
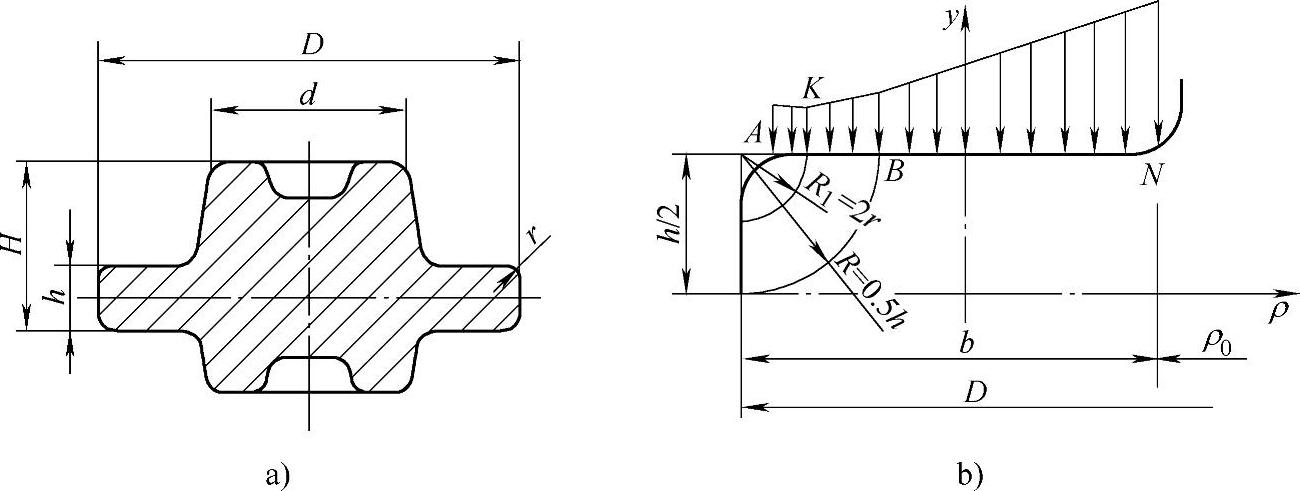
图2-47 变厚度圆形件环形部分正应力图
A-K区:该区宽度为2r(r为圆角半径),其正应力可近似取为
σy1≈-2σs (2-46)
K-B区:该区宽度为0.5h-2r,其正应力可利用巴布科夫(A.A.Bokob)等人研究圆环闭式镦粗所得的公式确定,即
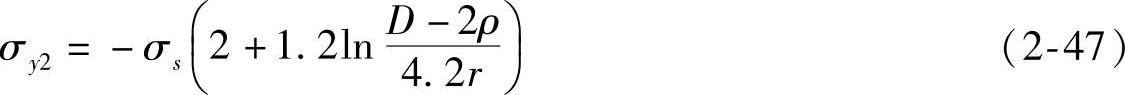
B-N区:正应力分布方程可利用圆柱体镦粗的一般公式,根据边界条件求出积分常数,将积分常数代回一般公式可得:
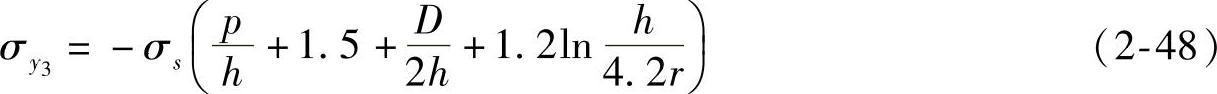 (https://www.xing528.com)
(https://www.xing528.com)
将式(2-46)~(2-48)作成图2-47b所示的应力分布曲线,再利用曲线所包围的体积,即可求出上述各区的变形力:
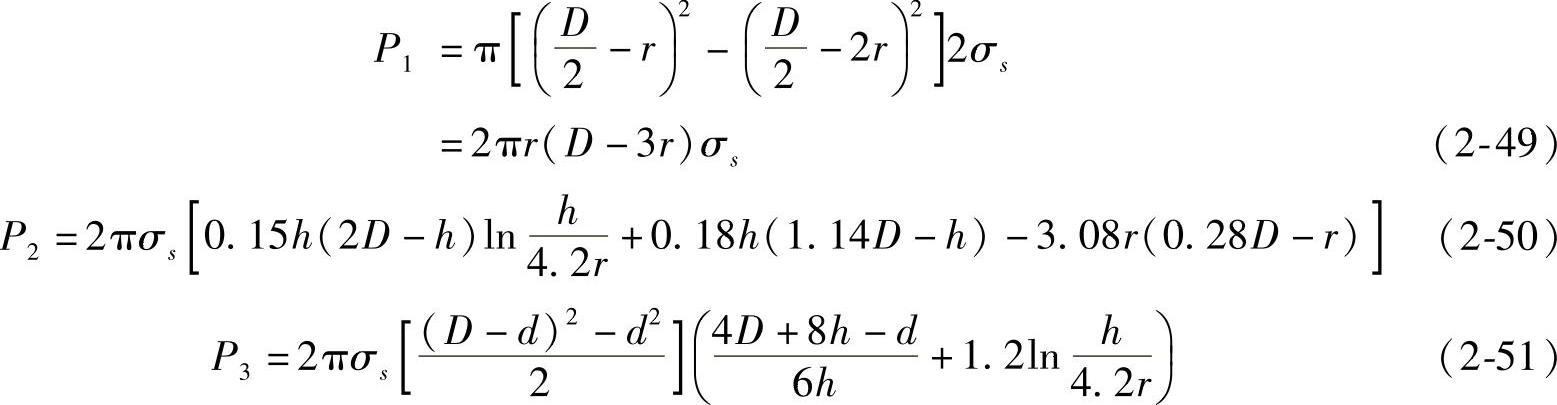
若令式(2-50)方括号内的表达式为M,式(2-51)中2πσs后的表达式为A,则环形区闭式模锻所需的力为
Pk=2πσs[(D-3r)r+M+A] (2-52)
锻件中心部分的模锻力可按开式模锻时求本体部分变形力的方法进行计算。此时,高度为h的圆环相当于飞边,所以中心部分正应力公式为

式中 h0——中心部分强烈变形区高度;当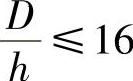 时,h0=0.15d+0.5h;当
时,h0=0.15d+0.5h;当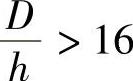 时,h0=2.9h。
时,h0=2.9h。
由边界条件σs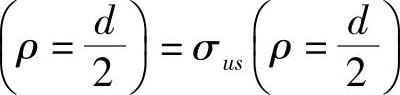 ,得
,得
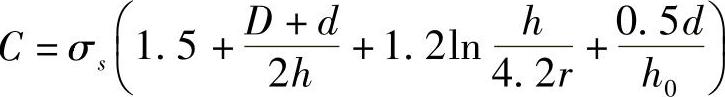
将C代入式(2-53),最后得
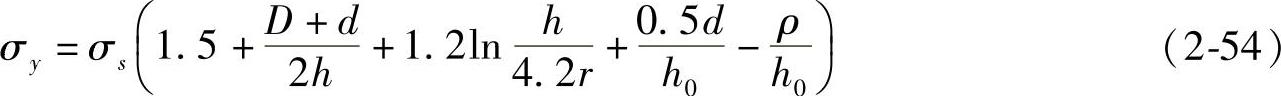
将上式积分,即得锻件中心部分的变形力:
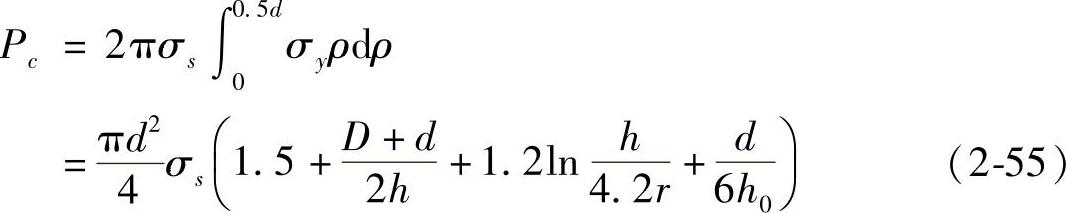
令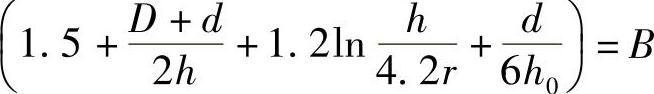 ,则由式(2-52)和式(2-55)得总的闭式模锻力:
,则由式(2-52)和式(2-55)得总的闭式模锻力:
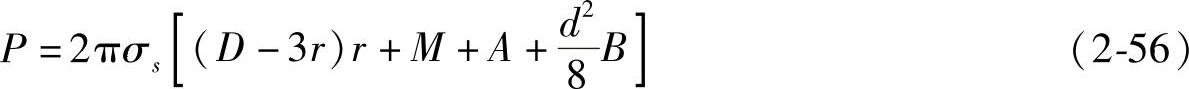
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




