具有平面法兰或局部球形粗大的锻件,其闭式模锻时金属流动过程可分为三个阶段:自由镦粗、法兰成形和充满角隙。
对于具有复杂冠状的齿轮锻件,其预锻工步中金属的流动同带法兰类锻件第二阶段变形特征相同。图2-41所示为这两类锻件闭式模锻时的上限法流动模型。图2-41a为第一阶段变形金属的流动情况,在这一阶段即自由流动阶段,区域Ⅰ已完全被金属充满,在进一步的变形中I区只作刚性平移,区域Ⅳ是不移动的刚性区,区域Ⅱ内的金属被挤入法兰环腔时受到区域Ⅲ的限制,区域Ⅲ内的金属受区域Ⅱ径向扩张力作用不断向法兰环形腔边缘流动。图中,虚线为实际边界线,为了简化变形过程的数学描述,将区域Ⅰ扩大而区域Ⅳ缩小,即用实线所表示的边界。这样一来,Ⅱ区的体积保持不变,法兰部分的流动尺寸h1、a与冲头位移Δh的关系能确定为H/R0和R0间的函数。
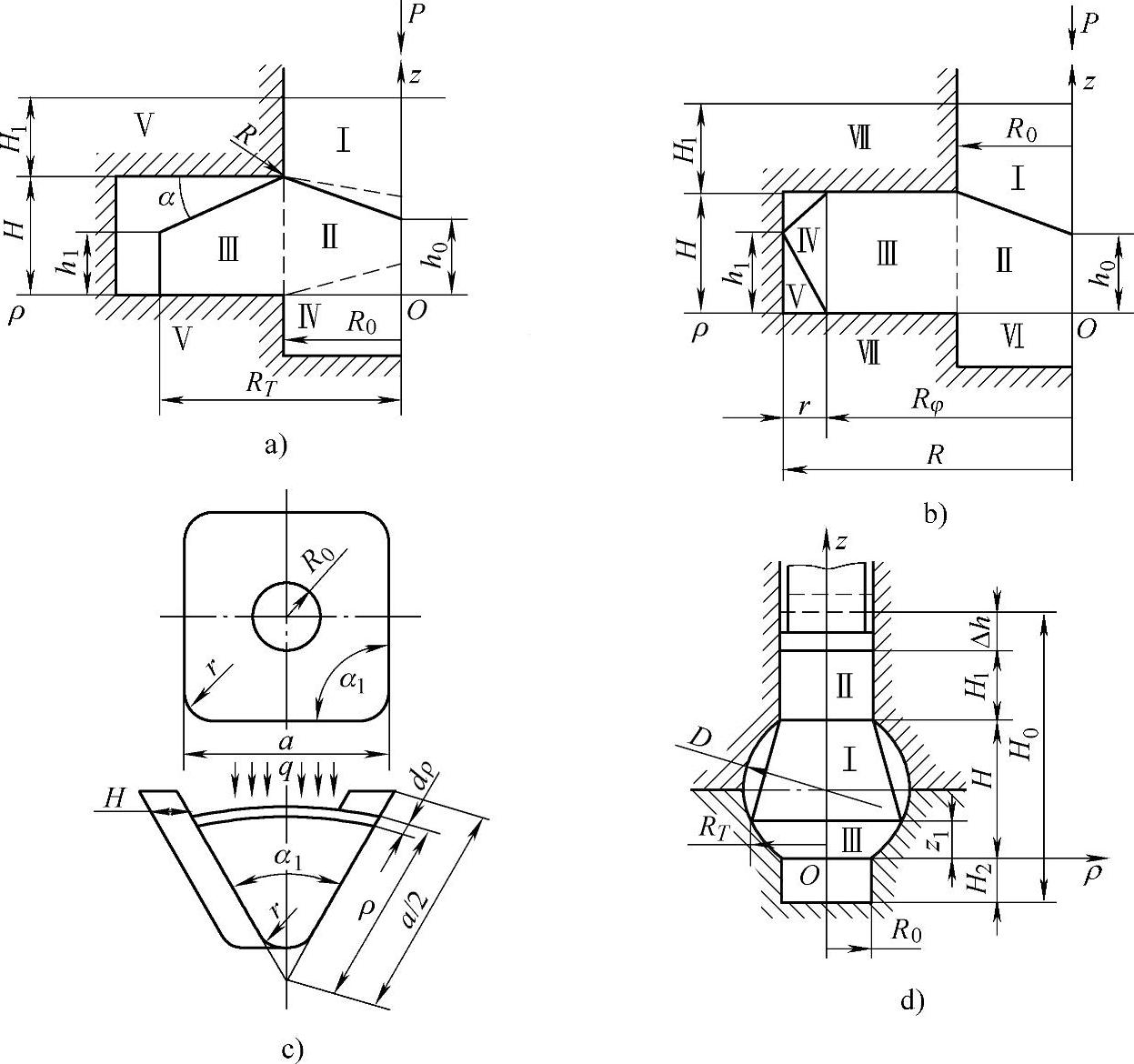
图2-41 变形区分布
对于带圆盘形法兰的轴对称锻件和带冠状齿轮的制坯工序,利用所提及的关系来设计预成形模膛,利用该模膛成形的中间毛坯可使终锻时的成形力减小,模膛寿命提高。此外,还可保证中间毛坯的法兰轮廓与终锻模膛的对应轮廓成等距离分布。
对于这类锻件,闭式模锻时冲头上的单位成形力可用式(2-33)计算:
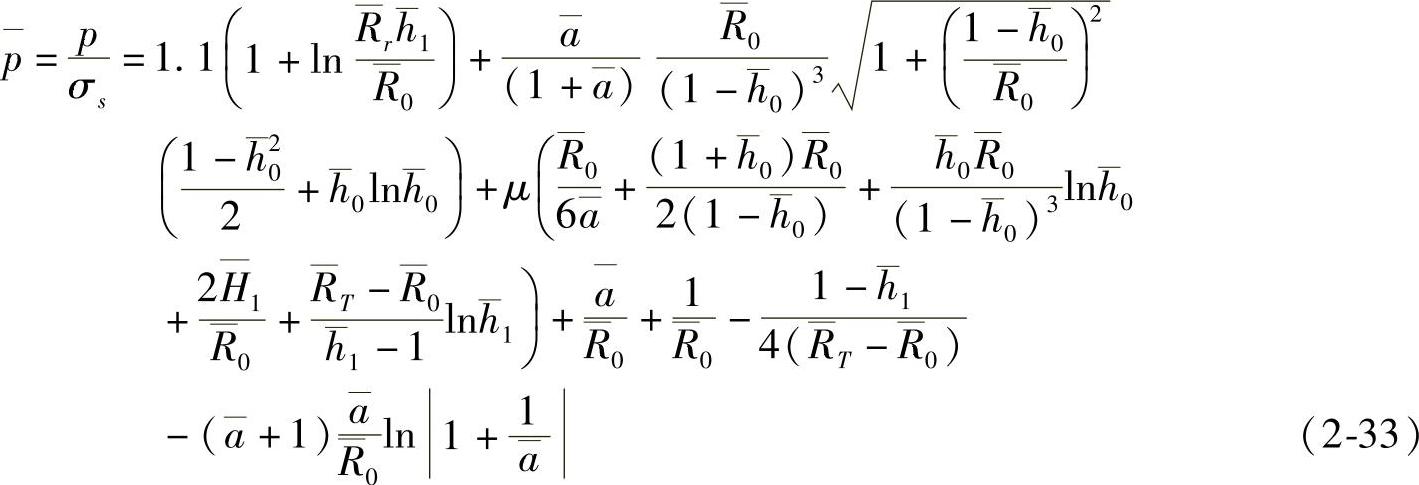
式中 σs——锻件材料的流动应力;
p,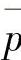 ——作用在冲头上的绝对和相对单位力;
——作用在冲头上的绝对和相对单位力;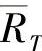 ,
,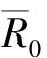 ,
,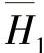 …——RT,R0,H1…(见图2-41a)相对于法兰高度H的相对尺寸;
…——RT,R0,H1…(见图2-41a)相对于法兰高度H的相对尺寸;
μ——接触面上的摩擦系数;
a——变形参数。
变形参数 由Ⅱ区的最小功条件求出,
由Ⅱ区的最小功条件求出,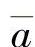 与
与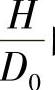 的关系如下:
的关系如下:
对于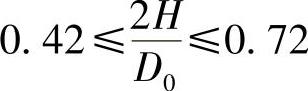 ,
,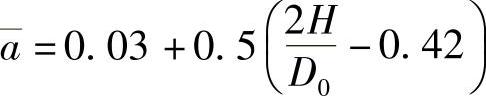 ;
;
对于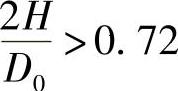 ,
,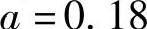 。
。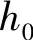 由图2-42确定。
由图2-42确定。
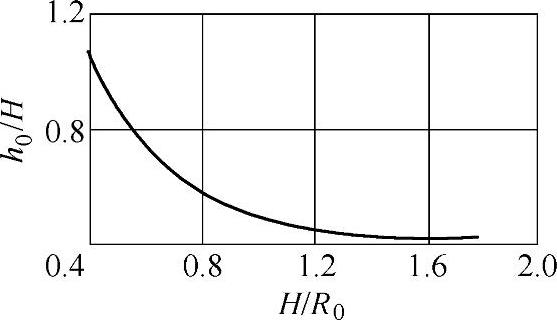
图2-42 变形区高度同锻件相对高度间的关系曲线
当模锻有平面法兰的轴对称锻件时,充满角部模膛时的情况如图2-41b所示。此时,其单位压力可用式(2-34)计算:
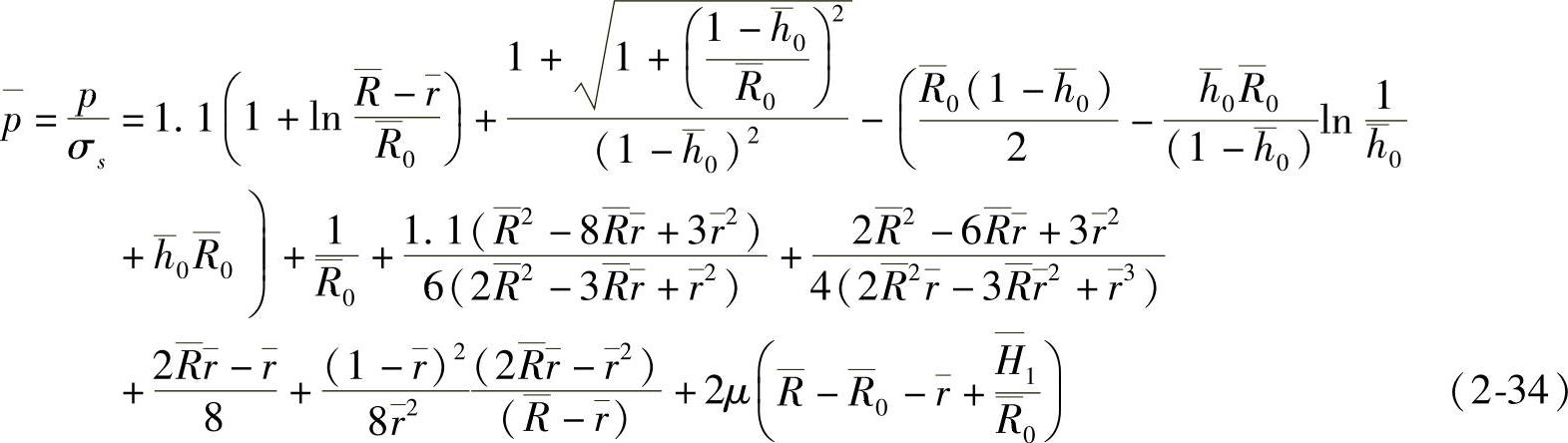 (https://www.xing528.com)
(https://www.xing528.com)
当模锻有非圆对称法兰的锻件时,如模锻带正多边形法兰锻件(见图2-41c),为充满法兰角部所必须的单位力,能够用功平衡法确定:
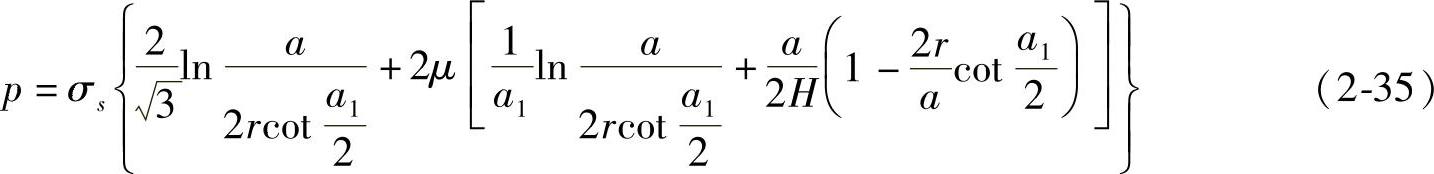
式中,正多边形的角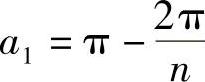 ,n为正多边形的边数。
,n为正多边形的边数。
对于具有椭圆形法兰的锻件,其角度a1按杆类锻件确定,利用q值作边界条件,求得冲头上的单位压力为

当模锻有球形粗大部分的锻件时,可采用图2-41d来分析。塑性变形区Ⅰ呈截锥形,底半径等于RT,上半径等于R0,高度等于锥体高H-z1。
区域Ⅱ和Ⅲ被认为是刚性的,随着球形模膛的充满,塑性变形区的下边界向上移动,因为锥高和它的底半径不断变化,形成的锥体是直边。塑性变形区内的应力表达式为
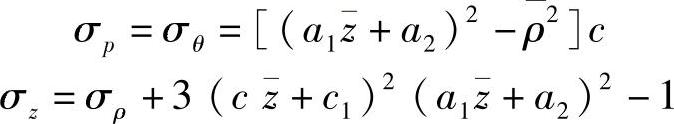
式中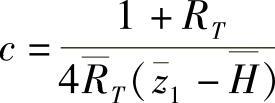 ;c1=(0.25+Hc);
;c1=(0.25+Hc);
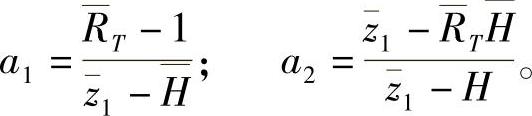
式中的所有相对尺寸均是对工件筒半径R0之比值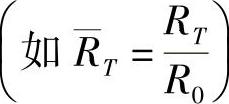 。
。
模锻这种锻件所需总变形力为
P=Pp+Pf(2-37)
式中 Pp——使金属发生塑性变形所需的力;
Pf——克服接触摩擦所需的力。
当z=H时,对σz积分可得:
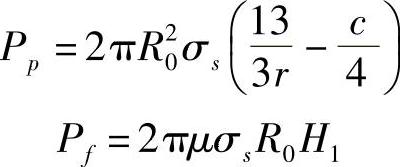
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




