【摘要】：内半径为Ri、外半径为R0、高度为H的圆环的闭式镦粗如图2-33所示。已知压力pi作用于环的内表面，下面是求圆环闭式镦粗所需变形力p的方法。图2-33 圆环的闭式镦粗满足运动条件并使坯料体积不变的速度场为应变速率为应力偏量为式中 K——材料常数，即材料屈服时的最大切应力；f——系数，取决于变形金属所选择的本构关系F。
内半径为Ri、外半径为R0、高度为H的圆环的闭式镦粗如图2-33所示。冲头下移的速度为v，凹模静止不动。已知压力pi作用于环的内表面，下面是求圆环闭式镦粗所需变形力p的方法。
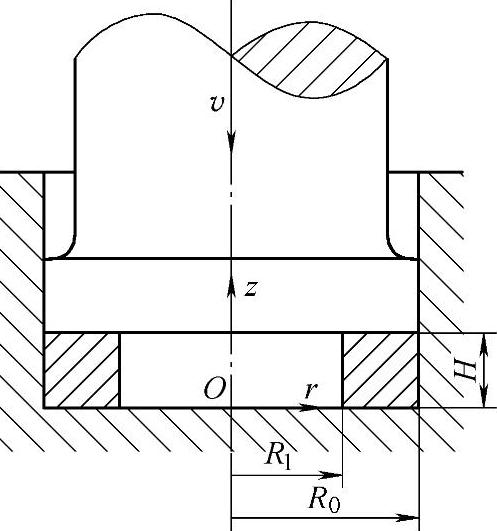
图2-33 圆环的闭式镦粗
满足运动条件并使坯料体积不变的速度场为
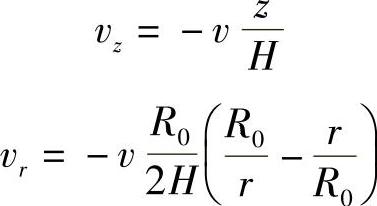
应变速率为
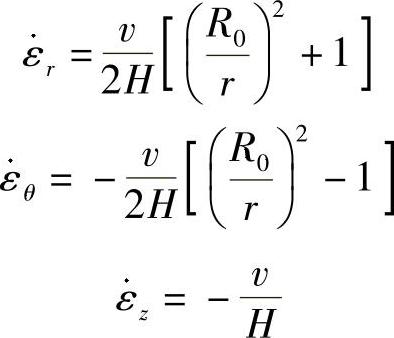
应力偏量为
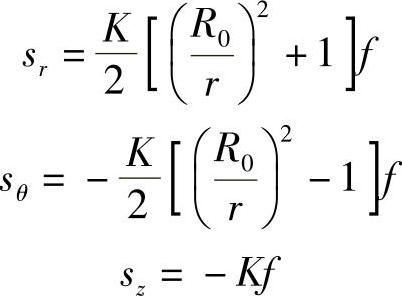
式中 K——材料常数，即材料屈服时的最大切应力；
f——系数，取决于变形金属所选择的本构关系F。
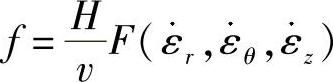
对应于四种模型的本构关系F分别为
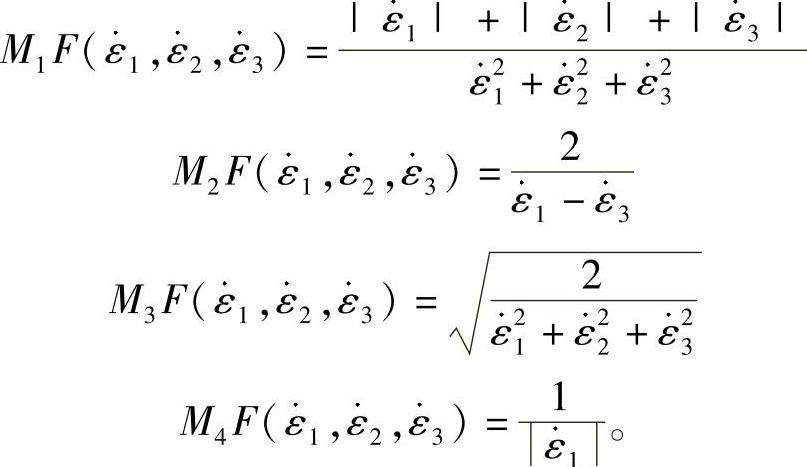
由平衡方程计算出r方向的应力分量为
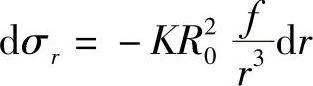
对上式积分，并代入边界条件r＝Ri时，σr＝pi，得到一般结果为
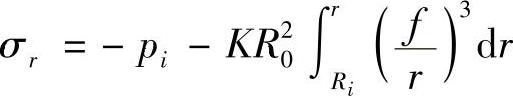
根据作用于冲头端面上力的平衡，得单位成形力的一般解为
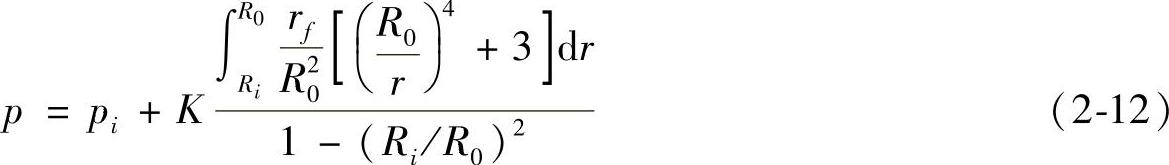
将其应用于四种模型材料M1、M2、M3、M4中。对于模型M1有
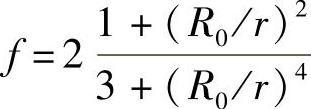
将f值代入式（2－12），得(https://www.xing528.com)
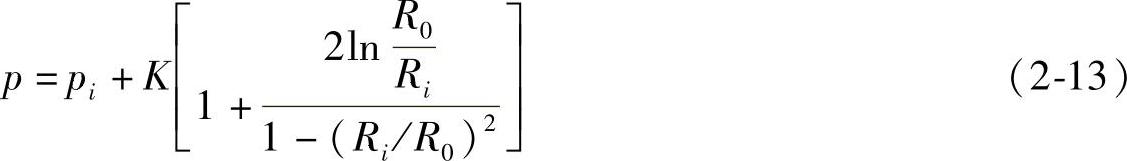
对于模型M2，最大的应变速度永远是εr，而最小的是εθ还是εz取决于圆环的几何尺寸。当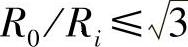
时，任何处的εz都是最小应变速度，并且有
f＝4／［（R0／r）2＋3］
将f值代入式（2-12），得
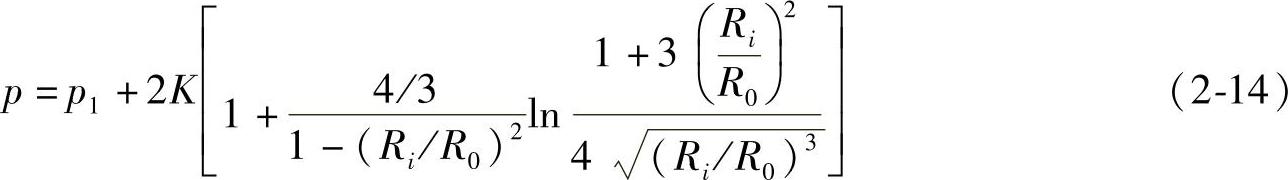
当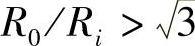
时，式（2-14）仅适用于区域
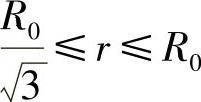中。另外，εθ为最小应变速度，并有
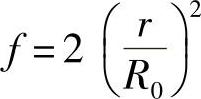
将原来f的表达式代入平均压力的方程中，求得
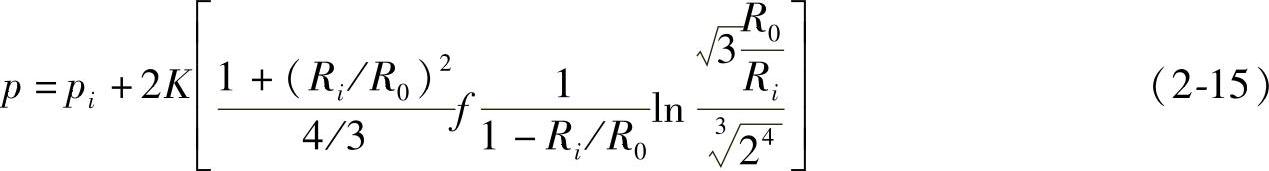
对于Mises材料即模型Ms，有
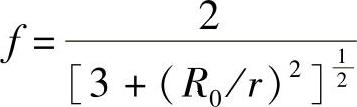
将其代回式（2-12），得
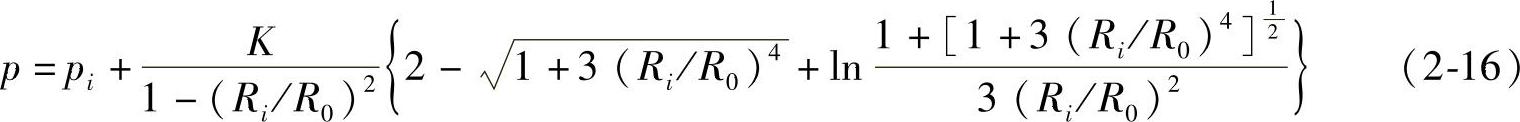
最后，对于模型M4有
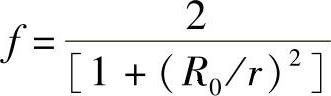
将其代回式（2-12），得
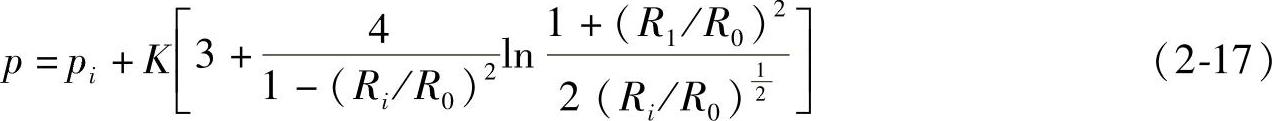
无论哪种模型，其总的变形力为
P＝pA
式中 A——镦粗结束时圆环的横截面积；
p——对应模型的单位变形力。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
