解决组合逻辑电路中的竞争与冒险问题

前面进行组合逻辑电路的分析与设计时，都没有考虑逻辑门的延迟时间对电路产生的影响。实际上，信号经过逻辑门电路都需要一定的时间。由于不同路径上门的级别不同，信号经过不同路径传输的时间不同，或者门的级别相同，而各个门延迟时间的差异，也会造成传输时间的不同。因此，电路在信号电平发生变换瞬间，可能与稳态下的逻辑功能不一致，产生错误输出，这种现象称为竞争—冒险。

1.产生竞争—冒险的原因

下面通过两个简单的电路的工作情况，说明产生竞争—冒险的原因。在图9.5.1（a）所示电路中，在稳态情况下，输出L始终为0。当A由0变为1时，由于反相器的延迟，的由1变0的变化会滞后A的变化，因此在很短的时间间隔内，与门的两个输入端均为1，使输出端出现一个正脉冲，工作波形如图9.5.1（b）所示。

图9.5.1　产生正跳变脉冲的竞争—冒险

同理，在图9.5.2（a）所示电路中，在稳态情况下，输出L始终为1。当A由1变为0时，由0变为1的变化会滞后A的变化，因此在很短的时间间隔内，或门的两个输入端均为0，使输出端出现一个负脉冲，工作波形如图9.5.2（b）所示。

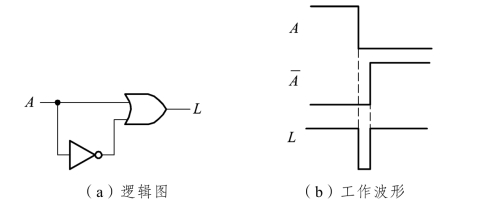
图9.5.2　产生负跳变脉冲的竞争—冒险

综上所述，一个逻辑门的两个输入端的信号同时向相反方向变化，而变化的时间有差异的现象，称为竞争。由竞争而可能产生输出干扰脉冲的现象称为冒险。值得注意的是，有竞争现象时不一定都会产生冒险现象。

2.竞争—冒险现象的判断方法

（1）代数法。

如果输出端的逻辑函数在一定条件下能简化成

则可判定存在竞争—冒险。

例9.5.1　判断是否存在竞争—冒险。

解：当A=B=1时，，因此C变量与变量经过的时间是不相同的，故L1存在竞争—冒险现象。

当A=B=1时，，由于A·B=1，所以L2始终为1，故L2不存在竞争—冒险现象。

（2）卡诺图法。(www.xing528.com)

除上述判断方法外，还可以用卡诺图进行判断。其具体做法是：首先画出逻辑函数的卡诺图，并画出和逻辑表达式中各“与”项对应的卡诺圈，若发现某两个卡诺圈存在“相切”关系，即两个卡诺圈之间存在不被同一卡诺圈包含的相邻最小项，则该电路可能产生竞争—冒险。

例9.5.2　已知某逻辑电路的逻辑表达式为试判断电路是否存在竞争—冒险。

解：画出给定函数L的卡诺图，并画出逻辑表达式中各“与”项对应的卡诺圈，如图9.5.3（a）所示。

图9.5.3　例9.5.2卡诺图

观察图9.5.3（a）所示卡诺图可发现，包含最小项m1、m3、m5、m7的卡诺圈和包含最小项m12、m13的卡诺圈中，m5和m13相邻，且m5和m13不被同一卡诺圈所包含，所以这两个卡诺圈“相切”。因此该电路存在竞争—冒险。这一结论也可用代数法进行验证，假定B=D=1，C=0，代入逻辑表达式可得，可见相应电路可能由于A的变化而产生冒险。

3.竞争—冒险现象的消除方法

（1）发现并消去互补乘积项。

例如：逻辑表达式，在B=C=0时，L=A·A，所以存在竞争—冒险。如果将该式变换为式

将消去，就不会出现竞争—冒险。

（2）增加乘积项以避免互补项相加。

在例9.5.2中，将输出逻辑表达式变为，卡诺图如图9.5.3（b）所示，当B=D=1，C=0时，就不会出现竞争—冒险。

（3）选通法。

可以在电路中加上一个选通信号，当输入信号变化时，输出端与电路断开，当输入稳定后，选通信号工作，使电路输出改变其状态。

（4）滤波法。

从实际的竞争冒险波形上可以看出，其输出的波形宽度非常窄，可以在输入端加上一个小电容来滤去其尖脉冲。

门电路的延时造成了竞争冒险现象，但是不是所有的竞争冒险都必须加以消除呢？答案是否定的。竞争冒险现象虽然会导致电路的误动作，但由于一般门电路的延时为纳秒（ns）数量级，这对于慢速电路来说，不会产生误动作，只有当电路的工作速度与门电路的最高工作速度在同一个数量级（或者门电路的延时与信号的周期在同一个数量级）时，竞争冒险才必须加以消除。