1.1位加法器
（1）半加器。
能对两个1位二进制数相加而求得和及进位的逻辑电路称为半加器。半加器只考虑两个1位二进制数的相加，而不考虑来自低位的进位数。
按照二进制加法运算规则可以列出半加器的真值表如表9.4.9所示。其中A和B为两个加数，C为进位输出，S为和数。
表9.4.9 半加器的真值表
由真值表可得到逻辑表达式
由表达式可画出半加器的逻辑图，如图9.4.17所示。
（2）全加器。
全加器能进行被加数、加数和来自低位的进位信号相加，并根据求和结果给出该位的进位信号。根据全加器的功能，可列出它的真值表，如表9.4.10所示。其中A和B分别为被加数和加数，Ci为低位的进位，S为本位和数，Co为向高位的进位数。
图9.4.17 半加器
表9.4.10 全加器的真值表
(www.xing528.com)
由表9.4.10可写出S和Co的逻辑表达式为
由上述的逻辑表达式可画出全加器逻辑电路图和符号图，如图9.4.18所示。
图9.4.18 全加器
2.多位加法器
实现多位二进制数相加的电路称为多位加法器。根据进位方式不同，有串行进位加法器和超前进位加法器两种。
（1）4位串行进位加法器。
把4个全加器依次级联起来，便可构成4位串行进位加法器，如图9.4.19所示。
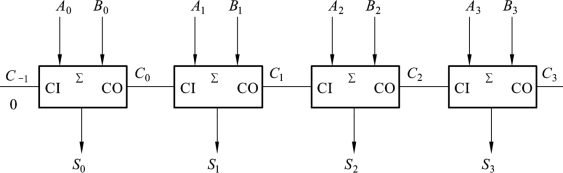
图9.4.19 4位串行进位加法器
这种加法器的优点是电路简单、连接方便；缺点是运算速度不高。由图9.4.19所示逻辑图不难理解，最高位的运算，必须等到所有低位运算依次结束，送来进位信号之后才能进行，因此其运算速度受到限制。为了提高加法运算速度，可采用超前进位方式。
（2）超前进位加法器。
所谓超前进位加法器，就是在做加法运算时，每位的进位只由被加数和加数决定，而与低位的进位无关。74HC283是4位超前进位加法器，如果进行更多位数的加法，则需要进行扩展。图9.4.20为用2片74HC283构成的8位二进制加法器。该电路把低位片（1）进位输出连接到高位片（2）进位输入，所以级间仍是串行进位方式，当级联数目增加时，会影响运算速度。
图9.4.20 8位二进制加法器
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
