数据选择器的应用与优化

数据选择器是一种多输入、单输出的组合逻辑电路，其逻辑功能是从多路输入数据中选择一路数据送到输出端。输出对输入的选择是受选择控制变量控制的，通常，对于一个具有N（2nN=）路输入和一路输出的数据选择器，应有n个选择控制变量，控制变量的每一种取值组合对应选中一路输入送至输出。常用的数据选择器有2选1数据选择器、4选1数据选择器、8选1数据选择等。

8选1数据选择器74LS151逻辑符号如图9.4.11所示。其中D0～D7为8个数据输入端，A0、A1、A2为3个选择控制输入端，为使能输入端，Y和为两个互补的输出端。

74LS151的真值表如表9.4.6所示。由真值表可知，在使能输入为1时，选择器不工作，输出Y为0；在使能输入为0时，选择器工作。工作情况如下：

当A2A1A0=000时，Y=D0；A2A1A0=001时，Y=D1；…A2A1A0=110时，Y=D6；A2A1A0=111时，Y=D7。其输出表达式为

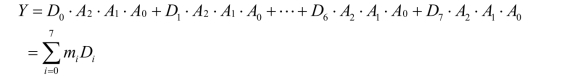
式中，im为选择控制变量A2、A1、A0组成的最小项，Di为i端的输入数据。

类似地，可以写出2n路数据选择器的输出表达式

式中，im为选择控制变量An1-、An-2、…、A1、A0组成的最小项，Di为2n路输入中的第i路数据输入。

图9.4.11　8选1数据选择器74LS151

表9.4.6　8选1数据选择器的真值表

例9.4.4　试用两片8选1数据选择器74LS151组成16选1数据选择器。其中16个数据输入端为D0～D15、4个选择控制输入端为A3、A2、A1、A0，输出端为Y和Y。

解：利用使能输入端很容易扩展数据选择器的功能。用两片74LS151连接起来构成16选1数据选择器的逻辑图如图9.4.12所示。图中两个芯片的使能输入端信号相反，片1的使能输入端接A3，片2的使能输入端接。当选通控制输入端A3A2A1A0为0×××时，片1工作，对应数据D0～D7被选送出去；当选通控制输入端A3A2A1A0为1×××时，片2工作，对应数据D8～D15被选送出去。例如：当A3A2A1A0=0101时，在使能输入端的作用下，片1工作，对应选通控制输入端A2A1A0=101的D5数据被送到或门输入端；片2由于使能输入端无效，输出信号为0，因此或门的输出信号为Y=0+D5=D5，完成了16选1的任务。

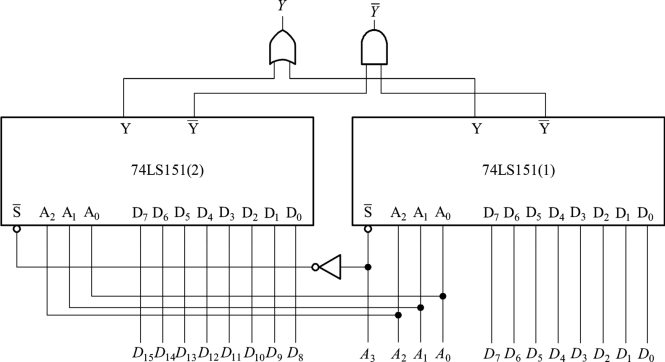
图9.4.12　例9.4.4逻辑图

由数据选择器的工作原理可知，数据选择器输出函数的逻辑表达式是一个组合逻辑表达式。如8选1数据选择器的输出函数的逻辑表达式为

而任何一个组合逻辑函数都可用最小项之和来表示，所以可以用数据选择器来产生逻辑函数的全部最小项，再配合用适当的门电路，即可实现组合逻辑函数。下面通过举例说明如何利用数据选择器来实现组合逻辑函数。

例9.4.5　用数据选择器实现逻辑函数

(www.xing528.com)

解：由于该函数有3个输入变量，所以可采用8选1数据选择器和4选1数据选择器实现。

方案一：采用8选1数据选择器。

因为8选1数据选择器的输出函数表达式为

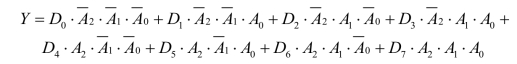
给定函数

比较上述两个表达式可知，要使Y=L，只需令A2=A，A1=B，A0=C且D1=D2=D4=D7=1，而D0=D3=D5=D6=0即可。所以，根据分析可作出用8路数据选择器实现给定函数的逻辑图，如图9.4.13（a）所示。

方案一给出了用具有n个选择变量的数据选择器实现n变量函数的一般方法：

首先将函数转换为最小项之和的形式，然后将函数的n个变量依次连接到数据选择器的n个选择控制输入端，最后将函数表达式中最小项对应的数据输入端接1，剩下的数据端接0。

方案二：采用4选1数据选择器。

因为4选1数据选择器的输出函数表达式为

给定函数

比较上述两个表达式可知，要使Y=L，只需令即可。由此，可作出用4选1实现给定函数的逻辑图，如图9.4.13（b）所示。

方案二给出了用具有n-1个选择变量的数据选择器实现n变量函数的一般方法：

首先从函数的n个变量中任选n-1个变量作为数据选择器的选择控制变量，然后根据所选定的选择控制变量将函数变换成

的形式，以确定各数据输入Di。假定剩余变量为X，则Di的取值只可能是0、1、X或四者之一。

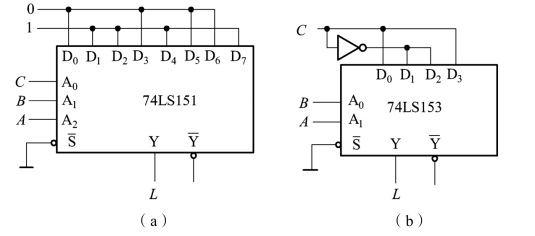
图9.4.13　例9.4.5例题