数制转换：理解进制的转换方式

1.二进制数转换成十进制数

由二进制数的一般表达式可知，只要将每一位二进制数与其权相乘，然后相加便可得到相应的十进制数。

例7.2.1　试将（110.01）2转换成十进制数。

解：（110.01）2=1 ×22+1 ×21+0 ×20+0 ×2-1+1 ×2-2=（6.25）10

2.十进制数转换成二进制

十进制数转换成二进制数时，要将整数部分和小数部分分别转换。

（1）整数部分的转换。

整数部分的转换采用除2取余法。所谓除2取余法即用2去除十进制整数，第一次除所得的余数为二进制数的最低位，把得到的商再除以2，所得余数为二进制数的次低位，依次类推，直至商为0时，所得余数为二进制数的最高位。

例7.2.2　试将（37）10转换成二进制数。

解：

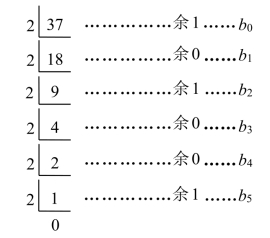
所以，（37）10=（100101）2

注意：在写结果时，不要将高位和低位写反了。

（2）小数部分的转换。

小数部分的转换是采用乘2取整法。所谓乘2取整法即用该小数乘以2，所得结果的整数部分为二进制数小数部分的最高位，其小数部分再乘以2，所得结果的整数部分为二进制数的第二位，依次类推，直至小数部分为0或达到要求精度为止。

例7.2.3　试将（0.423）10转换成二进制数（保留4位小数）。

解：

0.423×2=0.846……0……b-1

0.846×2=1.692……1……b-2(https://www.xing528.com)

0.692×2=1.384……1……b-3

0.384×2=0.768……0……b-4

0.768×2=1.536……1……b-5

提示保留4位小数，则第5位小数采取“零舍一入”的原则。

所以，（0.432）10=（0.0111）2。

从例7.2.3可知，小数转换时，有时不能用二进制小数精确地表示出来，这时只能根据精度要求，求到一定的位数，近似地表示。

3.二进制数与十六进制数之间的转换

由于16=24，所以4位二进制数对应1位十六进制数（对应关系见表7.2.1）。因此二进制数转换成十六进制数时，只要将二进制数按4位分组，每一组用1位十六进制数表示，即可实现它们之间的转换。

例7.2.4　试将二进制数（10110100111100.100101111）2转换成十六进制数。

解：将二进制数按4位分组，每一组用相应的十六进制数代替即得相应的十六进制数

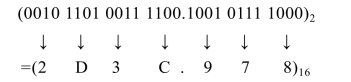
例7.2.5　试将十六进制数（3AF6.5B）16转换成二进制数。

解：将每位十六进制数用4位二进制数代替得到相应的二进制数

4.二进制数与八进制数之间的转换

同理，对于八进制数，可将3位进制数分为一组，对应于1位八进制。例如：

至于十进制数转换为十六进制数（或八进制数），可先将十进制数转换为二进制数，再将二进制数转换为十六进制数（或八进制数）。