比例运算电路原理及应用介绍

1.反相比例运算电路

（1）基本电路。

反相比例运算电路如图5.3.1所示，由于反馈网络与输入端为电流相加减方式，当输出为零时，反馈电阻Rf上的电流为零，从瞬时极性法判断，当反相输入端输入为正极性时，输出为负极性，通过Rf反馈到输入端为负极性，从以上分析可知，这是一个典型的电压并联负反馈电路。同相输入端通过电路补偿电阻R′接地，通常为了保证集成运放输入级差分放大电路的对称性R′=R //Rf。

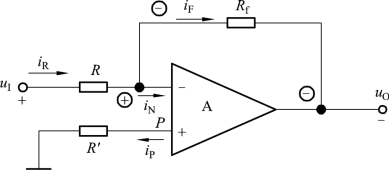
图5.3.1　反相比例运算电路

根据“虚断”的概念可得

故可认为R′上无电压降，相当于P点开路，uP与地等电位，得

又根据“虚短”的概念，同相输入端与反相入端电位相同，可知

节点N的电流方程为

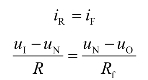
将式（5.3.1）代入上式可得

从式（5.3.2）可知，输入电压uI与输出电压uO，比例关系系数为-Rf/R。

从电路可以看出，这是一个反相比例运算电路，由于电路引入了深度电压负反馈，所以该电路的输出电阻Ro=0，由于引入的是并联反馈，所以输入电阻等于输入端和地之间的等效电阻，即Ri=R。在精确计算时应考虑输入电阻减小对运算电路的影响。

（2）T型网络反相比例运算电路。

在实际应用中，为了得到较大的电压放大倍数，而又不想Rf太大，一般采用T型网络取代图5.3.1所示电路中的Rf。如图5.3.2所示电路中，Rf由电阻R2、R3、和R4构成，形似英文字母，故称为T形网络电路。

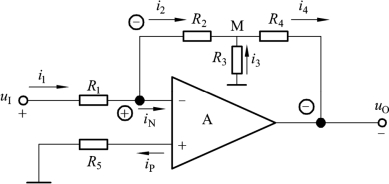
图5.3.2　T型网络反相比例运算电路

根据“虚断”的概念可得

故可认为R5上无电压降，相当于P点开路，uP与地等电位，得

又根据“虚短”的概念，同相输入端与反相输入端电位相同，可知

节点N的电流方程为

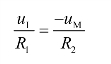
因而节点M的电位

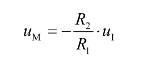
R3和R4的电流分别为

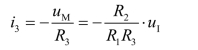
输出电压

将各电流表达式代入，整理可得

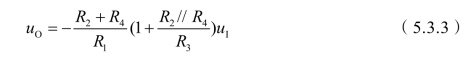
2.同相比例运算电路

（1）基本电路。

如图5.3.3所示的电路为同相比例运算电路，由于反馈网络与输入端为电压相加减方式，当输出为零时，反馈电阻Rf上的电流为零，从瞬时极性法判断，当同相输入端输入为正极性时，输出为正极性，通过Rf反馈到输入端为正极性。从以上分析可知，这是电压串联负反馈电路，输入电阻等于集成运放输入电阻（无穷大），输出电阻为零。

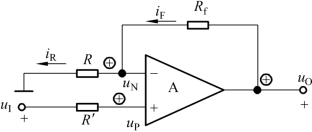
图5.3.3　同相比例运算电路

根据“虚断”的概念得

所以R′上无压降，故(www.xing528.com)

根据“虚短”的概念得

说明集成运放的净输入电压为零，但有共模输入电压。

因而iR=if，即

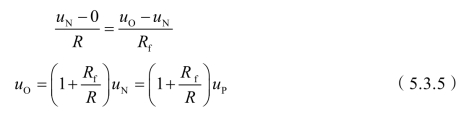
将式（5.3.4）代入得

从上式可知uO与uI同相且放大倍数大于1。由于存在共模输入信号，所以在误差分析时，应重点考虑共模信号对同相比例放大电路的影响。

（2）电压跟随器。

在同相比例运算电路中，若将输出电压的全部反馈到反相输入端，就构成了图5.3.4所示的电压跟随器。电路5.3.4引入了电压串联负反馈，且反馈系数为1。由于uO=uN=uP，故输出电压与输入电压的关系为

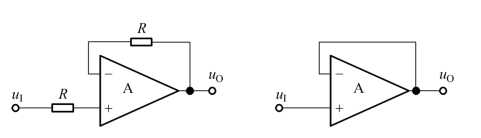
图5.3.4　电压跟随器

理想运放的开环差模增益为无穷大，因而电压跟随器具有比射极输出器好很多的跟随特性。

综上所述，对于单一信号作用的运算电路，在分析运算关系时，应首先列出关键节点的电流方程，所谓关键节点是指那些与输入电压和输出电压产生关系的节点，如N点和P点；然后根据“虚短”和“虚断”的原则，进行整理，即可得到输出电压和输入电压的运算关系。

例5.3.1　电路如图5.3.5所示，已知R2＞＞ R4，R1=R2试问：

（1）uO与uI的比例系数为多少？

（2）若R4开路，则uO与uI的比例系数为多少？

图5.3.5　例5.3.1的电路图

解：比较图5.3.5和图5.3.2所示的电路不难发现，它们是完全相同的运算电路，即T形网络反相比例运算电路。

（1）由于uN=uP=0，因而

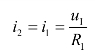
M点的电位

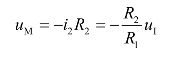
由于R2＞＞R4，可以认为

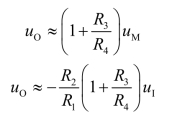
在上式中，由于R1=R2，故uO与uI的关系式为

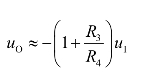
所以，比例系数约为-（1+R3/R4）。

（2）若R4开路，则电路变为典型的反相比例运算电路，uO与uI的运算关系式为：

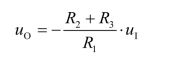
由于R1=R2，故比例系数为-（1+R3/R1）。

例5.3.2　电路如图5.3.6所示，已知集成运放输出的最大幅值为±14 V；uO=-55uI，其余参数如图中所标注。回答下列问题：

（1）求出R5的值；

（2）若uI与地接反，则输出电压与输入电压的关系将产生什么变化？

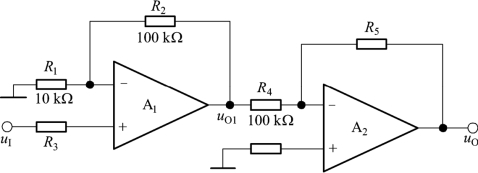
图5.3.6　例5.3.2的电路图

解：在图5.3.6所示电路中，A1构成同相比例运算电路，A2构成反相比例运算电路。

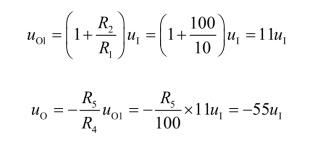
得出R5=500 kΩ。

（2）若uI与地接反，则第一级变为反相比例运算电路。因此，

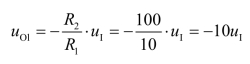
由于第二级电路的比例系数仍为-5，所以uO=50uI。