【摘要】:将代入上式得图2-21 固定平行平板间隙流动又因为压差流动:上下两平板固定不动,液体在间隙两端压差作用下而在间隙中流动。由边界条件:y=0时,u=0;y=h时,u=v0及dp/dx=-Δp/l,可得2)两平板既有相对运动,两端又有压差的流动。当完全偏心时,e=h,ε=1,此时的泄漏量是同心时的2.5倍。
1.平行平板的间隙流动
有如下几种情况。
(1)固定平行平板间隙流动(压差流动)(见图2-21)
微小单元体dxdy的受力平衡方程为
pdy+(τ+dτ)dx=(p+dp)dy+τdx
对上式两次积分得
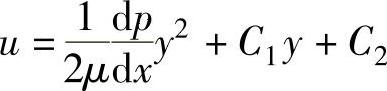
C1、C2为积分常数。
将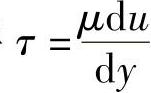 代入上式得
代入上式得
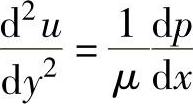
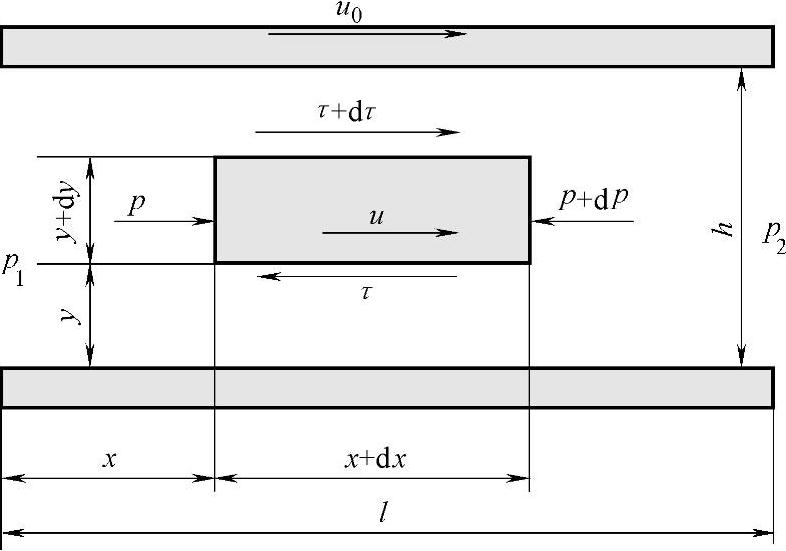
图2-21 固定平行平板间隙流动
又因为压差流动:上下两平板固定不动,液体在间隙两端压差作用下而在间隙中流动。由边界条件:y=0时,u=0;y=h时,u=0及dp/dx=-Δp/l,可得
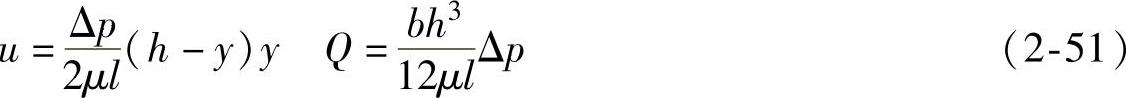
(2)平行平板有相对运动时的间隙流动
1)纯剪切流动:两平板有相对运动速度v,但无压差。
由边界条件:
y=0时,u=0;y=h时,u=v0及dp/dx=-Δp/l,可得(https://www.xing528.com)
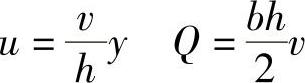
2)两平板既有相对运动,两端又有压差的流动。以上两种的线形叠加:
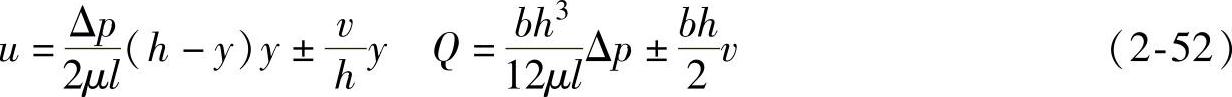
以上两式中的正负号确定:长平板相对短平板运动方向与压差流动方向一致时,取“+”;反之,取“-”。
2.圆柱环形间隙流动有如下几种情况。
(1)同心环形间隙在压差作用下的流动(见图2-22)

(2)偏心环形间隙在压差作用下的流动(见图2-23)
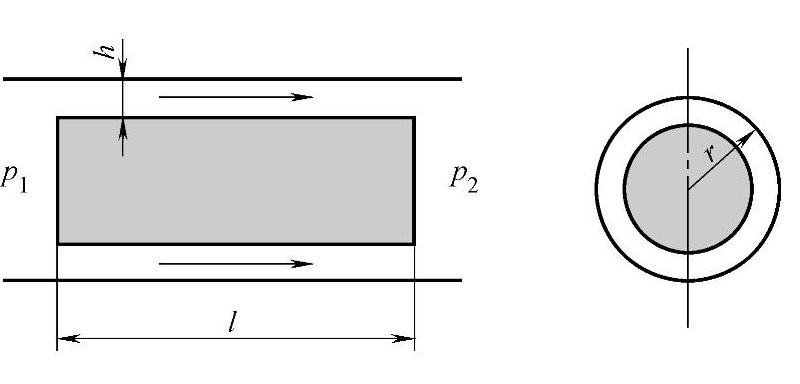
图2-22 同心环形间隙在压差作用下的流动
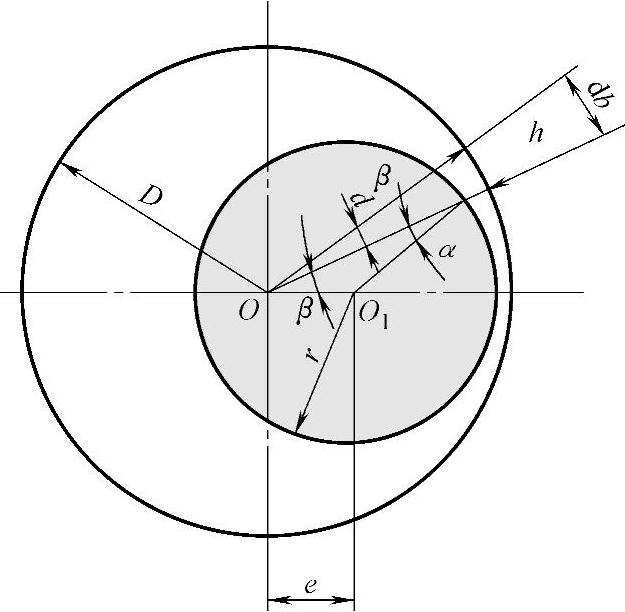
图2-23 偏心环形间隙在压差作用下的流动


从上式可知,通过同心圆环形间隙的流量公式(2-53)只不过是ε=0时偏心圆环形间隙流量公式的特例。当完全偏心时,e=h,ε=1,此时的泄漏量是同心时的2.5倍。
(3)内外圆柱表面有相对运动又存在压差的流动
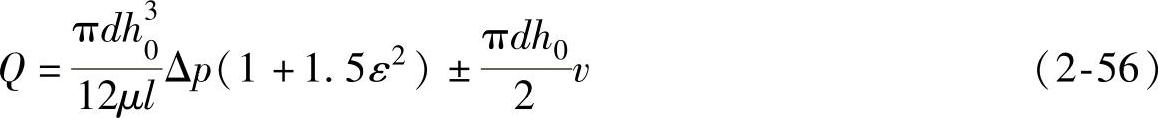
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




