液体动力学中的定常流动及伯努利方程分析

1.液体运动的基本概念

（1）理想液体

既无粘性又不可压缩的液体称为理想液体（实际液体则既有粘性又可压缩）。

（2）定常流动

液体流动时，若液体中任何一点的压力、速度和密度都不随时间而变化，则这种流动就称为定常流动。否则，只要压力、速度和密度有一个量随时间变化，则这种流动就称为非定常流动。

（3）一维流动

当液体整个作线形流动时，称为一维流动。

（4）流线、流束和通流截面（见图2-12）

1）迹线：流动液体的某一质点在某一时间间隔内在空间的运动轨迹。

2）流线：表示某一瞬时，液流中各处质点运动状态的一条条曲线。在此瞬时，流线上各质点速度方向与该线相切。在定常流动时，流线不随时间而变化，这样流线就与迹线重合。由于流动液体中任一质点在其一瞬时只能有一个速度，所以流线之间不可能相交，也不可能突然转折。

3）流束：在一条的流动空间中任意画一不属流线的封闭曲线，沿经过此封闭曲线上的每一点作流线，由这些流线组合的表面称为流管。流管内的流线群称为流束。

4）通流截面：流束中与所有流线正交的截面称为通流截面。截面上每点处的流动速度都垂直于这个面。

5）平行流动：流线彼此平行的流动。

6）缓变流动：流线夹角很小或流线曲率半径很大的流动。平行流动和缓变流动都可算是一维流动。

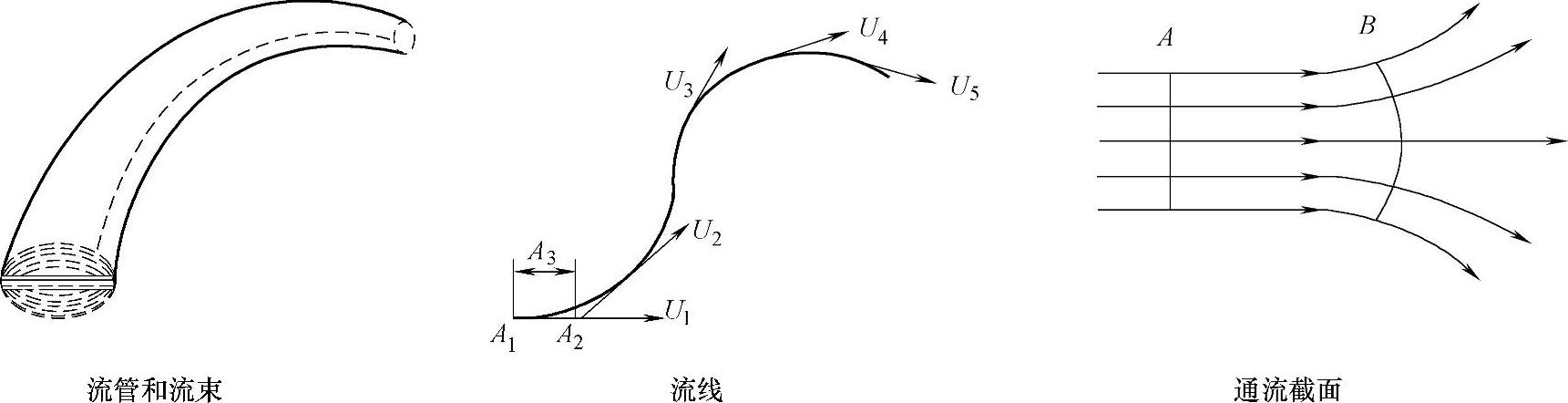
图2-12 流线、流束和通流截面

（5）流量和平均流速

单位时间内通过某通流截面的液体的体积称为流量。

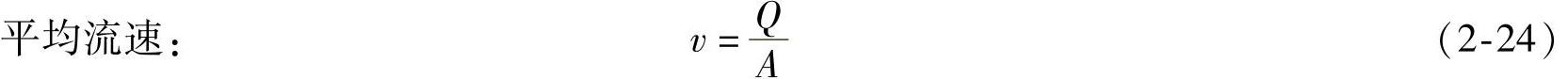
式中 v——平均流速；

Q——流量；

A——通流截面积。

（6）流动液体的压力

静止液体内任意点处的压力在各个方向上都是相等的，可是在流动液体内，由于惯性力和粘性力的影响，任意点处在各个方向上的压力并不相等，但数值相差甚微。当惯性力很小，且把液体当作理想液体时，流动液体内任意点处的压力在各个方向上的数值可以看做是相等的。

2.连续性方程

假设液体作定常流动，且不可压缩。任取一流管，两端通流截面面积为A₁、A₂，在流管中取一微小流束，流束两端的截面面积分别为dA₁和dA₂，在微小截面上各点的速度可以认为是相等的，且分别为v₁和v₂。根据质量守恒定律，在dt时间内流入此微小流束的质量应等于此微小流束流出的质量。连续性方程推导简图如图2-13所示：v₁dA₁dt=v₂dA₂dtv₁dA₁=v₂dA2对整个流管：

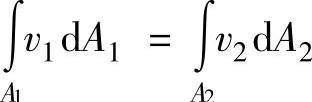
从而Q₁=Q₂，如用平均流速v表示，得v₁A₁=v₂A₂，由于通流截面是任意取的，故有

Q=vA=const （2-25）

上式称为不可压缩液体作定常流动时的连续性方程。它说明

1）通过流管任一通流截面的流量相等；

2）液体的流速与管道通流截面积成反比；

3）在具有分歧的管路中，有Q₁=Q₂+Q₃。

3.伯努利方程

伯努利方程就是能量守恒定律（动能定理）在流动液体中的表现形式。

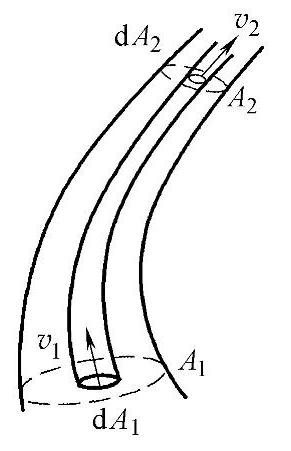
图2-13 连续性方程推导简图

（1）理想液体的运动微分方程

在微小流束上，取截面积为dA，长为ds的微元体，现研究理想液体定常流动条件下在重力场中沿流线运动时其力的平衡关系（见图2-14）。

微元体所受的重力为-ρgdAds，压力作用在两端面上的力为

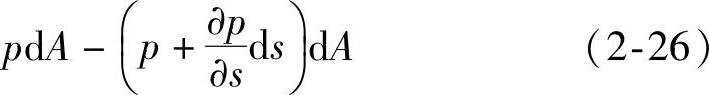(www.xing528.com)

微元体在定常流动下的加速度为

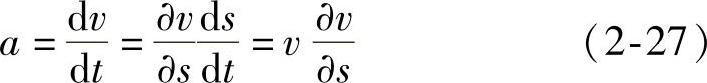
微元体的力平衡方程为

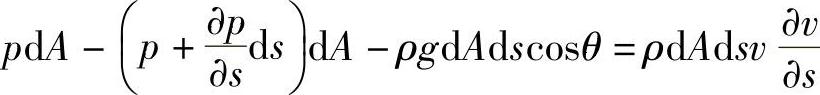
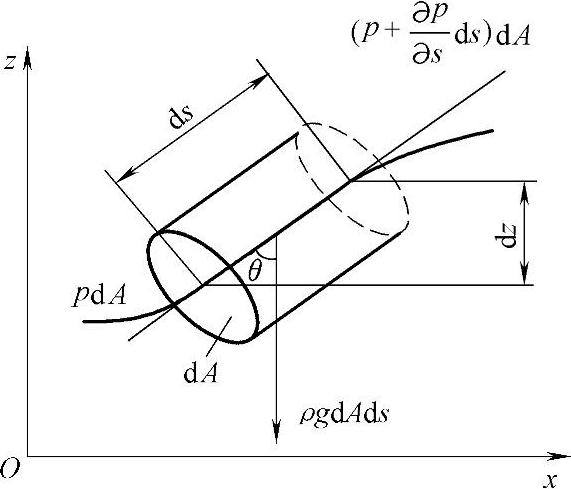
图2-14 流动液体上的作用力

上式简化后可得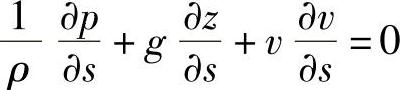

式中p，z，v只是s的函数，进一步简化得

上式即为重力场中，理想液体沿流线作定常流动时的运动方程，即欧拉运动方程。

（2）理想液体的伯努利方程沿流线对欧拉运动方程积分得上式两边同除以g得

以上两式即为理想液体作定常流动的伯努利方程，如图2-15所示。第一项为单位重量液体的压力能称为比压能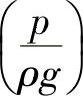；第二项为单位重量液体的动能称为比动能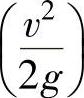；第三项为单位重量液体的位能称为比位能（z）。

由于上述三种能量都具有长度单位，故又分别称为压力水头、速度水头和位置水头。这三者的和是一常量，称为总水头，用H表示。伯努利方程的物理意义：在密封管道内作稳定流动的理想液体具有三种形式的能量，即压力能、动能和位能，三者之间可以互相转换，并且液体在管道内任一处这三种能量的总和为一定值。这就是伯努利定律，也称为理想液体作定常流动时的能量守恒定律。而静压力基本方程则是伯努利方程（在速度为零时）的特例。

（3）实际液体流束的伯努利方程

实际液体都具有粘性，因此液体在流动时还需克服由于粘性所引起的摩擦阻力，这必然要消耗能量，设因粘性消耗的能量为h′_w，则实际液体微小流束的伯努利方程为

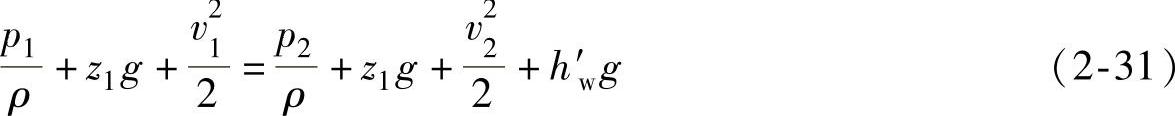
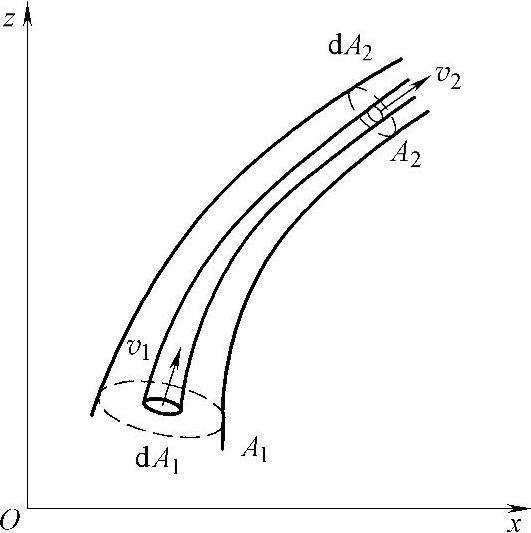
图2-15 伯努利方程推导简图

实际液体流束的伯努利方程推导简图如图2-16所示。

（4）实际液体总流的伯努利方程

将微小流束扩大到总流，由于在通流截面上速度v是一个变量，若用平均流速代替，则必然引起动能偏差，故必须引入动能修正系数。于是实际液体总流的伯努利方程为

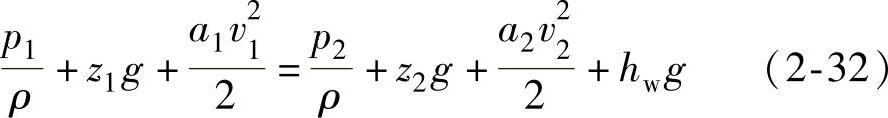
将式（2-8）代入式（2-32）中得

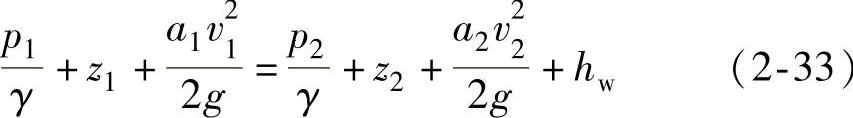
式中 h_w——由液体粘性引起的能量损失。

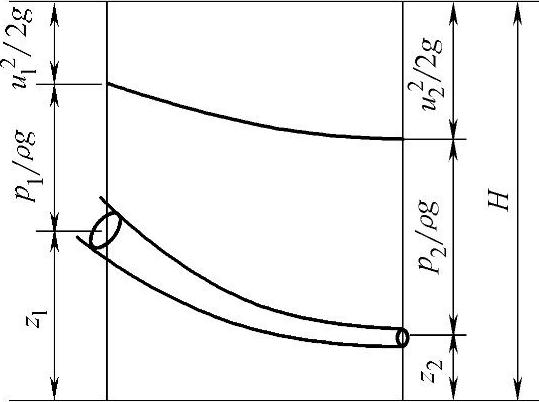
图2-16 实际液体流束的伯努利方程推导简图

4.动量方程

液体作用在固体壁面上的力，用动量定理来求解比较方便。动量定理：作用在物体上的力的大小等于物体在力作用方向上的动量的变化率（见图2-17），即

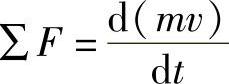
取分离体：

微元的动量变化是：

d（mv）=d（mv）_2-2-d（mv）_1-1=ρdQdt（v₂-v₁）

微小流束扩大到总流，对液体的作用力合力为

∑F=ρQ（v₂-v₁）

将微小流束扩大到总流，对液体的作用力合力为

∑F=ρQ（β₂v₂-β₁v₁） （2-34）

式中 β₁、β₂——动量修正系数，一般在紊流时β=1，层流时β=1.33。

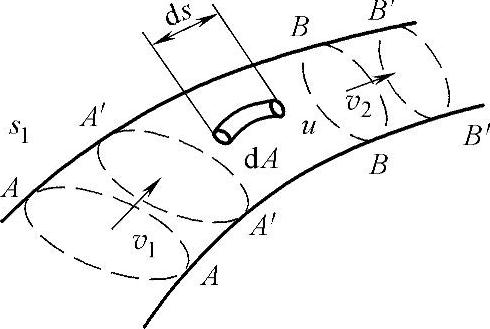
图2-17 液流动量方程推导简图