【摘要】:直线P0—P0在圆R0上做纯滚动,直线P0—P0上的任一点A,在平面上所描绘的轨迹AB即为渐开线。P0—P0称为渐开线的发生线,以R0为半径的圆称为渐开线的基圆,B点称为渐开线发生线相对于基圆滚动时的瞬时中心,如图5-158所示。以R0为半径的圆称即为渐开线的基圆,直线AB为B点的曲率半径。从渐开线的形成原理可知:基圆大小不同,其渐开线形状也不同,所以渐开线形状完全取决于基圆的大小。
直线P0—P0在圆R0上做纯滚动,直线P0—P0上的任一点A,在平面上所描绘的轨迹AB即为渐开线。P0—P0称为渐开线的发生线,以R0为半径的圆称为渐开线的基圆,B点称为渐开线发生线相对于基圆滚动时的瞬时中心,如图5-158所示。
BM=AM=R0φ=R0(Q+α)
又 BM=R0tanα
故 R0tanα=R0(Q+α)
tanα=Q+α
Q=tanα-α(rad)——渐开线函数
B点的极坐标 ρB=R0/cosα
B点的曲率半径 RB=R0tanα
渐开线坐标方程 X=R0(sinφ-φcosφ)(https://www.xing528.com)
Y=R0(φsinφ+cosφ)
在铣床上,有一个半径为R0的圆台紧靠在工作台上的平板侧面上(X0—X0),圆台逆时针做无滑动的纯滚动,则圆台上的A0在平面上所描绘的曲线BA0即为渐开线(图5-159)。
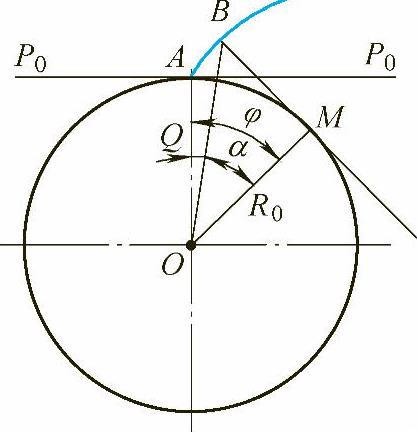
图5-158 渐开线形成原理图
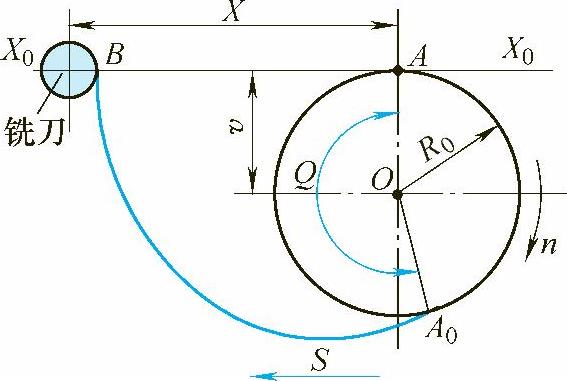
图5-159 铣渐开线原理图
如果立铣刀距圆台滚动的终点A的距离为AB+r(r铣刀半径),圆台顺时针做纯滚动返回到A点,则立铣刀即可在平板上铣出一个渐开线形面。以R0为半径的圆称即为渐开线的基圆,直线AB为B点的曲率半径。从渐开线的形成原理可知:基圆大小不同,其渐开线形状也不同,所以渐开线形状完全取决于基圆的大小。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




