控制单个关节的方法

采用常规技术，通过独立控制每个连杆或关节来设计机器人的线性反馈控制器是可能的。重力及各关节间的互相作用力的影响，可由预先计算好的前馈来消除。为了减少计算工作量，补偿信号往往是近似的，或者采用简化计算公式来获得。

1.位置控制系统结构

现在市场上供应的工业机器人，其关节数为3～7个。最典型的工业机器人具有6个关节，存在6个自由度，带有夹手。辛辛那提˙米拉克龙T3、尤尼梅逊的PUMA650和斯坦福机械手都是具有6个关节的工业机器人，并分别由液压、气压或电气传动装置驱动。其中，斯坦福机械手具有反馈控制功能，它的一个关节控制方框图如图6-10所示。从图6-10可见，它有一个光学编码器，与测速发电机一起组成位置和速度反馈系统。这种工业机器人是一种定位装置，它的每个关节都有一个位置控制系统。

如果不存在路径约束，那么控制器只要知道夹手要经过路径上所有指定的转弯点就够了。控制系统的输入是路径上所需要转弯点的笛卡儿坐标，这些坐标点可能通过两种方法输入，即

（1）以数字形式输入系统；

（2）以示教方式供给系统，然后进行坐标变换，即计算各指定转弯点在笛卡儿坐标系中的相应关节坐标[q1，q2，…，q6]，计算方法与坐标点信号输入方式有关。

对于数字输入方式，对f-1[q1，q2，…，q6]进行数字计算；对于示教输入方式，进行模拟计算。其中，f-1[q1，q2，…，q6]为f[ q1，q2，…，q6]的逆函数，而f [q1，q2，…，q6]为含有6个坐标数值的矢量函数。最后，对机器人的关节坐标点逐点进行定位控制。假如允许机器人依次只移动一个关节，而把其他关节锁住，那么每个关节控制器都很简单。如果多个关节同时运动，那么各关节间力的相互作用会产生耦合，使控制系统变得复杂。

2.单关节控制器的传递函数

把机器人看作刚体结构。图6-11给出了单关节的电动机-齿轮-负载联合装置示意图。图中：Ja为单关节的驱动电动机转动惯量；Jm为单关节的夹手负载在传动端的转动惯量；JL为机械手连杆的转动惯量；Bm为传动端的阻尼系数；BL为负载端的阻尼系数；θm为传动端角位移；θL为负载端角位移。另外，Nm，NL分别为传动轴和负载上的齿轮齿数；rm，rL分别为传动轴和负载轴上的齿轮节距半径；η为减速齿轮传动比，η=rm/rL=Nm/NL。令F为从电动机传至负载的作用在齿轮啮合点上的力，则

图6-10　斯坦福机械手的一个关节控制方框图

TL′为折算到电动机轴上的等效负载力矩，而且

又因为θm=2π/Nm，θL=2π/NL，所以

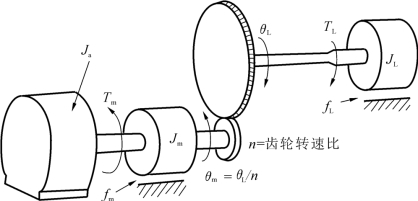
图6-11　单关节的电动机-齿轮-负载联合装置示意图

传动侧和负载侧的角速度及角加速度关系如下：

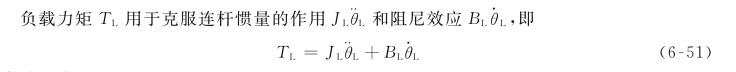
或者改写为

在传动轴一侧，同理可得

从而有

或

式中：J——传动轴上的等效转动惯量，J=Jeff=JL+Jm+η2JL；

B——传动轴上的等效阻尼系数，B=Beff=Bm+η2BL。

根据电枢控制直流电动机的传递函数，若Vm表示电枢回路电压，Lm表示电枢回路电感，Rm表示电枢回路电阻，KI表示转矩常数，ke为考虑电动机转动时产生反电动势的系数，得到相似的传递函数如下：

故相应地，其拉氏变换为

式中：Kθ——变换系数。

图6-12（a）给出了这种位置控制器的方框图。从式（6-57）至式（6-63）可得开环传递函数为

由于实际上ωLm＜＜Rm，因此可以忽略式（6-64）中含有Lm的项，式（6-64）也就简化为

再求闭环传递函数：

图6-12　机械手位置控制器结构

对某台具体的机器人来说，其特征参数（η，KI，Kt，ke，Rm，J和B等）的数值是由部件的制造厂家提供的，或者通过实验测定。

值得注意的是，变换常数Kθ和放大器增益K1必须根据相应的机器人结构谐振频率和阻尼系数来确定。电动机必须克服电动机-测速机组的平均摩擦力矩fm、外加负载力矩T1、重力矩Tg，以及离心作用力矩Tc。这些物理量表示实际附加负载对机器人的作用。把这些作用插到图6-12（b）所示位置控制器方框图中电动机产生有关力矩的作用点上，即可得图6-12（c）所示的控制方框图。图中，Fm（s），TL（s）和Tg（s）分别为fm，T1和Tc的拉氏变换变量。

3.参数确定及稳态误差(www.xing528.com)

1）Kθ和K1的确定

据式（6-68），闭环传递函数可写为

因此，闭环系统的特征方程为

一般把式（6-70）表示为

这时

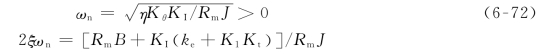
于是可得

令Keff为机器人关节的有效刚度，ωr为关节结构谐振频率，ω表示有效惯量为Jeff的关节测量接受谐振频率，则

对于一个谨慎的安全系数为200%的设计，必须设定自然振荡角频率ωn不大于结构谐振频率ωr的一半。据式（6-72）和式（6-74）可得

化简得

由此确定了Kθ的上限。

下面讨论K1变化范围。实际上，要防止机器人的位置控制器处于低阻尼工作状态，必须要求ξ≥1。根据式（6-73），有

将式（6-75）代入，得

因为J值随负载变化，所以K1的下限也随之相应变化。为简化控制器设计，必须固定放大器的增益。于是，把最大的J值代入式（6-77），就不会出现欠阻尼系统。

2）关节控制器的稳态误差

在图6-12（c）中，由于引入fm、T1、Tc等实际附加负载，使控制器的闭环传递函数发生了变化，因此必须推导出新的闭环传递函数。由图6-12（c）可知：

式（6-78）未考虑离心作用。又由图6-12（c）可知：

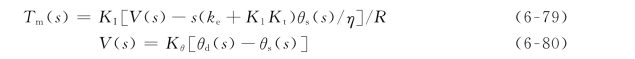
经代数运算后得

式中：

无论什么时候，当Fm（s），TL（s）和Tg（s）消失时，式（6-82）就简化成为式（6-71）。因为

所以根据式（6-81），可得

当负载为恒值时，TL=CL，又fm=Cf和Tg=Cg也均为恒值，所以TL（s）=CL/s，Fm（s）=CL/s，Tg（s）=Cg/s，而且式（6-83）变换为

式中的X（s）取代了θd（s），以表示广义输入指令。

应用终值定理：

能够确定稳态误差。

当输入为一恒定位移C0时，

于是可得稳态位置误差为

位置控制器的稳态位置误差，可按要求的补偿力矩信号限制在允许范围内。

应用自动控制的一般原理与方法，还可以分析控制器的稳态速度误差和加速度误差。